Small parameter, method of the
in the theory of differential equations
A method for constructing approximate solutions of differential equations and systems depending on a parameter.
1. The method of the small parameter for ordinary differential equations.
Ordinary differential equations arising from applied problems usually contain one or more parameters. Parameters may also occur in the initial data or boundary conditions. Since an exact solution of a differential equation can only be found in very special isolated cases, the problem of constructing approximate solutions arises. A typical scenario is: the equation and the initial (boundary) conditions contain a parameter 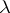 and the solution is known (or may be assumed known) for
and the solution is known (or may be assumed known) for 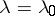 ; the requirement is to construct an approximate solution for values
; the requirement is to construct an approximate solution for values 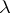 close to
close to 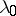 , that is, to construct an asymptotic solution as
, that is, to construct an asymptotic solution as 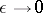 , where
, where 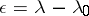 is a "small" parameter. The method of the small parameter arises, e.g., in the three-body problem of celestial mechanics, which goes back to J. d'Alembert, and was intensively developed at the end of the 19th century.
is a "small" parameter. The method of the small parameter arises, e.g., in the three-body problem of celestial mechanics, which goes back to J. d'Alembert, and was intensively developed at the end of the 19th century.
The following notations are used below:  is an independent variable,
is an independent variable,  is a small parameter,
is a small parameter, 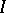 is an interval
is an interval 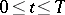 , and the sign
, and the sign 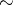 denotes asymptotic equality. All vector and matrix functions which appear in equations and boundary conditions are assumed to be smooth (of class
denotes asymptotic equality. All vector and matrix functions which appear in equations and boundary conditions are assumed to be smooth (of class 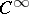 ) with respect to all variables in their domain (with respect to
) with respect to all variables in their domain (with respect to  for
for 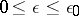 or
or  ).
).
1) The Cauchy problem for an  -th order system:
-th order system:
 | (1) |
Let the solution 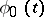 of the limit problem (that is, (1) with
of the limit problem (that is, (1) with 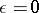 ) exist and be unique for
) exist and be unique for 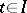 . Then there is an asymptotic expansion for the solution
. Then there is an asymptotic expansion for the solution 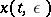 of (1) as
of (1) as 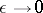 ,
,
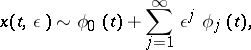 | (2) |
which holds uniformly with respect to 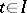 . This follows from the theorem on the smooth dependence on the parameter of the solution of a system of ordinary differential equations. If the vector functions
. This follows from the theorem on the smooth dependence on the parameter of the solution of a system of ordinary differential equations. If the vector functions 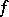 and
and 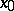 are holomorphic for
are holomorphic for 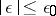 ,
, 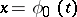 ,
, 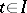 , then the series in (2) converges to a solution
, then the series in (2) converges to a solution 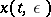 for sufficiently small
for sufficiently small 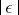 uniformly relative to
uniformly relative to 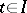 (Poincaré's theorem). Similar results hold for boundary value problems for systems of the form (1), if the solution of the corresponding limit problem exists and is unique.
(Poincaré's theorem). Similar results hold for boundary value problems for systems of the form (1), if the solution of the corresponding limit problem exists and is unique.
One distinguishes two forms of dependence of equations (or systems) on a small parameter — regular and singular. A system in normal form depends regularly on  if all its right-hand sides are smooth functions of
if all its right-hand sides are smooth functions of  for small
for small 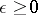 ; otherwise the system depends singularly on
; otherwise the system depends singularly on  . When the system depends regularly on
. When the system depends regularly on  , the solution of the problem with a parameter, as a rule, converges uniformly on a finite
, the solution of the problem with a parameter, as a rule, converges uniformly on a finite 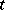 -interval as
-interval as 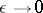 to a solution of the limit problem.
to a solution of the limit problem.
2) In the linear theory one considers  -th order systems which depend singularly on
-th order systems which depend singularly on  :
:
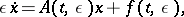 |
where the entries of the 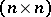 -matrix
-matrix  and the components of the vector
and the components of the vector  are complex-valued functions. The central problem in the linear theory is the construction of a fundamental system of solutions of the homogeneous system (that is, for
are complex-valued functions. The central problem in the linear theory is the construction of a fundamental system of solutions of the homogeneous system (that is, for 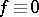 ), the asymptotic behaviour of which as
), the asymptotic behaviour of which as 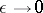 is known throughout the interval
is known throughout the interval 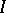 .
.
The basic result of the linear theory is the following theorem of Birkhoff. Let: 1) the eigenvalues 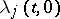 ,
, 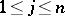 , of
, of  be distinct for
be distinct for 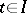 ; and 2) the quantities
; and 2) the quantities
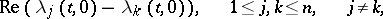 |
not change sign. Then there is a fundamental system of solutions  of the homogeneous system
of the homogeneous system
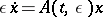 |
for which there is the following asymptotic expansion as 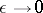 :
:
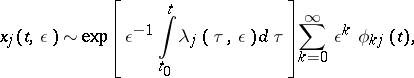 | (3) |
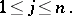 |
This expansion is uniform relative to 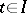 and can be differentiated any number of times with respect to
and can be differentiated any number of times with respect to 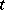 and
and  . If
. If  does not depend on
does not depend on  , that is,
, that is, 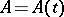 , then
, then
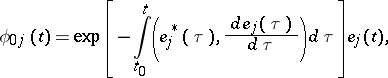 |
where 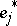 ,
, 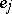 are left and right eigenvectors of
are left and right eigenvectors of 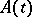 normalized by
normalized by
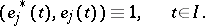 |
Solutions having asymptotic behaviour of the form (3) are called WKB solutions (see WKB method). The qualitative structure of these solutions is as follows. If
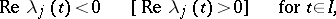 |
then  is a vector function of boundary-layer type for
is a vector function of boundary-layer type for  (
(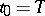 ), that is, it is noticeably different from zero only in an
), that is, it is noticeably different from zero only in an  -neighbourhood of
-neighbourhood of 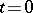 (
(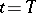 ). If, however,
). If, however, 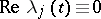 ,
, 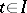 , then
, then 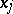 strongly oscillates as
strongly oscillates as 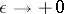 and has order
and has order 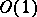 on the whole interval
on the whole interval 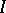 .
.
If 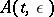 is a holomorphic matrix function for
is a holomorphic matrix function for 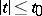 ,
, 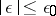 and condition 1) is satisfied, then (3) is valid for
and condition 1) is satisfied, then (3) is valid for 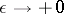 ,
, 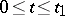 , where
, where  is sufficiently small. A difficult problem is the construction of asymptotics for fundamental systems of solutions in the presence of turning points on
is sufficiently small. A difficult problem is the construction of asymptotics for fundamental systems of solutions in the presence of turning points on  , that is, points at which
, that is, points at which 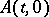 has multiple eigenvalues. This problem has been completely solved only for special types of turning points (see [1]). In a neighbourhood of a turning point there is a domain of transition in which the solution is rather complicated and in the simplest case is expressed by an Airy function (cf. Airy functions).
has multiple eigenvalues. This problem has been completely solved only for special types of turning points (see [1]). In a neighbourhood of a turning point there is a domain of transition in which the solution is rather complicated and in the simplest case is expressed by an Airy function (cf. Airy functions).
Similar results (see [1], [17]) are valid for scalar equations of the form
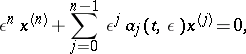 |
where 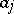 is a complex-valued function; the roles of the functions
is a complex-valued function; the roles of the functions 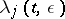 are played by the roots of the characteristic equation
are played by the roots of the characteristic equation
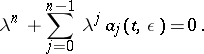 |
WKB solutions also arise in non-linear systems of the form
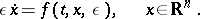 |
The WKB asymptotic expansion (3), under the conditions of Birkhoff's theorem, is valid in an infinite interval 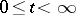 (that is, (3) is asymptotic both as
(that is, (3) is asymptotic both as  and as
and as 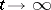 ) if
) if 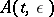 is sufficiently well behaved as
is sufficiently well behaved as 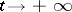 , for example, if it rapidly converges to a constant matrix with distinct eigenvalues (see [2]). Many questions of spectral analysis (see [3]) and mathematical physics reduce to singular problems with a small parameter.
, for example, if it rapidly converges to a constant matrix with distinct eigenvalues (see [2]). Many questions of spectral analysis (see [3]) and mathematical physics reduce to singular problems with a small parameter.
3) Of particular interest is the investigation of non-linear systems of the form
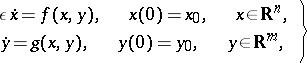 | (4) |
where 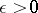 is a small parameter. The first equation describes fast motions, the second slow motions. For example, the van der Pol equation reduces by the substitution
is a small parameter. The first equation describes fast motions, the second slow motions. For example, the van der Pol equation reduces by the substitution
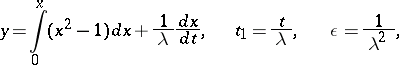 |
for 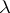 large, to the system
large, to the system
 |
which is of the form (4).
For 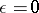 the equation of fast motion degenerates to the equation
the equation of fast motion degenerates to the equation 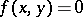 . In some closed bounded domain
. In some closed bounded domain 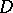 of the variable
of the variable 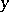 , let this equation have an isolated stable continuous root
, let this equation have an isolated stable continuous root 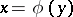 (that is, the real parts of the eigenvalues of the Jacobi matrix
(that is, the real parts of the eigenvalues of the Jacobi matrix 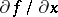 are negative for
are negative for  ,
, 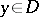 ); suppose that solutions of (4) and of the degenerate problem
); suppose that solutions of (4) and of the degenerate problem
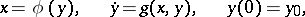 | (5) |
exist and are unique for  , and let for the function
, and let for the function 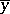 , obtained as the solution of (5),
, obtained as the solution of (5), 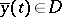 for
for 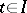 . If
. If 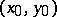 is in the domain of influence of the root
is in the domain of influence of the root 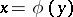 , then
, then
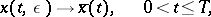 |
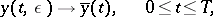 |
as 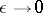 , where
, where 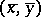 is the solution of the degenerate problem (Tikhonov's theorem). Close to
is the solution of the degenerate problem (Tikhonov's theorem). Close to  the limit transition
the limit transition 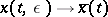 is non-uniform — a boundary layer occurs. For problem (4) there is the following asymptotic expansion for the solution:
is non-uniform — a boundary layer occurs. For problem (4) there is the following asymptotic expansion for the solution:
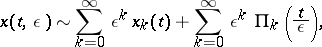 | (6) |
and the asymptotic expansion for 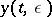 has a similar form. In (6) the first sum is the regular part and the second sum is the boundary layer. The regular part of the asymptotic expansion is calculated by standard means: series of the form (2) are substituted into (4), the right-hand sides are expanded as power series in
has a similar form. In (6) the first sum is the regular part and the second sum is the boundary layer. The regular part of the asymptotic expansion is calculated by standard means: series of the form (2) are substituted into (4), the right-hand sides are expanded as power series in  and the coefficients at equal powers of
and the coefficients at equal powers of  are equated. For the calculation of the boundary-layer part of the asymptotic expansion one introduces a new variable
are equated. For the calculation of the boundary-layer part of the asymptotic expansion one introduces a new variable  (the fast time) in a neighbourhood of
(the fast time) in a neighbourhood of 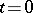 and applies the above procedure. There is an interval on the
and applies the above procedure. There is an interval on the 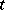 -axis on which both the regular (or outer) expansion and the boundary-layer (or inner) expansion are useful. The functions
-axis on which both the regular (or outer) expansion and the boundary-layer (or inner) expansion are useful. The functions 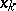 ,
, 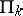 are defined by the coincidence of these expansions (the so-called method of matching, see [4], [5]).
are defined by the coincidence of these expansions (the so-called method of matching, see [4], [5]).
Similar results hold when the right-hand side of (4) depends explicitly on 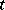 , for scalar equations of the form
, for scalar equations of the form
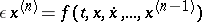 | (7) |
and for boundary value problems for such systems and equations (see Differential equations with small parameter, [6], [7]).
For approximation of the solution of (4) at a break point, where stability is lost (for example, where one of the eigenvalues of  for
for 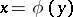 is zero), series of the form (5) lose their asymptotic character. In a neighbourhood of a break point the asymptotic expansion has quite a different character (see [8]). The investigation of a neighbourhood of a break point is particularly essential for the construction of the asymptotic theory of relaxation oscillations (cf. Relaxation oscillation).
is zero), series of the form (5) lose their asymptotic character. In a neighbourhood of a break point the asymptotic expansion has quite a different character (see [8]). The investigation of a neighbourhood of a break point is particularly essential for the construction of the asymptotic theory of relaxation oscillations (cf. Relaxation oscillation).
4) Problems in celestial mechanics and non-linear oscillation theory lead, in particular, to the necessity of investigating the behaviour of solutions of (1) not in a finite interval but in a large 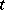 -interval of the order of
-interval of the order of 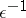 or higher. For these problems a method of averaging is widely applied (see Krylov–Bogolyubov method of averaging; Small denominators, [9]–[11]).
or higher. For these problems a method of averaging is widely applied (see Krylov–Bogolyubov method of averaging; Small denominators, [9]–[11]).
5) Asymptotic behaviour of solutions of equations of the form (7) has been investigated, in particular, with the help of the so-called method of multiple scales (see [4], [5]); this method is a generalization of the WKB method. An example of the method has been given using the scalar equation
 | (8) |
which has a periodic solution (see [12]). The solution is sought for in the form
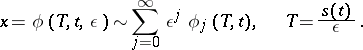 | (9) |
(The functions 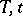 are called the scales.) If (8) is linear, then
are called the scales.) If (8) is linear, then 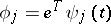 and (9) is a WKB solution. In the non-linear case the equations of the first two approximations take the form
and (9) is a WKB solution. In the non-linear case the equations of the first two approximations take the form
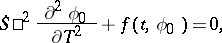 |
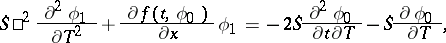 |
where the first equation contains two unknown functions 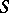 and
and 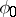 . Let this equation have a solution
. Let this equation have a solution 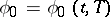 periodic in
periodic in 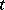 . Then the missing equation, from which
. Then the missing equation, from which 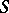 is to be determined, is found from the periodicity in
is to be determined, is found from the periodicity in 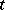 of
of 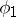 and has the form
and has the form
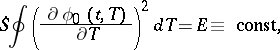 |
where the integral is taken over a period of 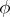 .
.
References
| [1] | W. Wasov, "Asymptotic expansions for ordinary differential equations" , Interscience (1965) |
| [2] | M.V. Fedoryuk, "Asymptotic methods in the theory of ordinary linear differential equations" Math. USSR Sb. , 8 : 4 (1969) pp. 451–491 Mat. Sb. , 79 : 4 (1969) pp. 477–516 |
| [3] | M.A. Naimark, "Linear differential operators" , 1–2 , Harrap (1968) (Translated from Russian) |
| [4] | J.D. Cole, "Perturbation methods in applied mathematics" , Blaisdell (1968) |
| [5] | A.H. Nayfeh, "Perturbation methods" , Wiley (1973) |
| [6] | A.B. Vasil'eva, V.F. Butuzov, "Asymptotic expansions of solutions of singularly perturbed equations" , Moscow (1973) (In Russian) |
| [7] | A.B. Vasil'eva, V.F. Butuzov, "Singularly perturbed equations in critical cases" , Moscow (1978) (In Russian) |
| [8] | E.F. Mishchenko, N.Kh. Rozov, "Differential equations with small parameters and relaxation oscillations" , Plenum (1980) (Translated from Russian) |
| [9] | N.N. Bogolyubov, Yu.A. Mitropol'skii, "Asymptotic methods in the theory of non-linear oscillations" , Hindushtan Publ. Comp. , Delhi (1961) (Translated from Russian) |
| [10] | V.M. Volosov, B.I. Morgunov, "Averaging methods in the theory of non-linear oscillatory systems" , Moscow (1971) (In Russian) |
| [11] | V.I. Arnol'd, "Small denominators and problems of stability of motion in classical and celestial mechanics" Russian Math. Surveys , 18 : 6 (1963) pp. 86–191 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 91–192 |
| [12] | G.E. Kuzmak, "Asymptotic solutions of nonlinear second order differential equations with variable coefficients" J. Appl. Math. Mech. , 23 (1959) pp. 730–744 Prikl. Mat. i Mekh. , 23 : 3 (1959) pp. 515–520 |
| [13] | A.A. Andronov, A.A. Vitt, A.E. Khaikin, "The theory of oscillators" , Dover, reprint (1987) (Translated from Russian) |
| [14] | G.E. Giacaglia, "Perturbation methods in non-linear systems" , Springer (1972) |
| [15] | N.N. Moiseev, "Asymptotic methods of non-linear mechanics" , Moscow (1969) (In Russian) |
| [16] | V.F. Butuzov, A.B. Vasil'eva, M.V. Fedoryuk, "Asymptotic methods in the theory of ordinary differential equations" Progress in Math. , 8 (1970) pp. 1–82 Itogi Nauk. Mat. Anal. 1967 (1969) pp. 5–73 |
| [17] | W. Wasow, "Linear turning point theory" , Springer (1985) |
N.Kh. RozovM.V. Fedoryuk
2. The method of the small parameter for partial differential equations.
As for ordinary differential equations, solutions of partial differential equations can regularly or singularly depend on a small parameter  (it is assumed that
(it is assumed that 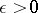 ). Roughly speaking, regular dependence is observed when the leading terms of the differential operator do not depend on
). Roughly speaking, regular dependence is observed when the leading terms of the differential operator do not depend on  , and the minor terms are smooth functions of
, and the minor terms are smooth functions of  for small
for small  . The solution is then also a smooth function of
. The solution is then also a smooth function of  . But if any of the leading terms vanish as
. But if any of the leading terms vanish as 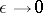 , then the solution, as a rule, depends singularly on
, then the solution, as a rule, depends singularly on  . In this case one often speaks of partial differential equations "with a small parameter in front of the leading derivatives" . Such a classification is somewhat arbitrary, since the choice of leading terms is not always obvious; also, the parameter itself may also occur in the boundary conditions. In addition, singularities may arise in unbounded domains, even when the small parameter only occurs in the minor derivatives (at infinity they play in a sense an equal, or even more major, role as the leading terms).
. In this case one often speaks of partial differential equations "with a small parameter in front of the leading derivatives" . Such a classification is somewhat arbitrary, since the choice of leading terms is not always obvious; also, the parameter itself may also occur in the boundary conditions. In addition, singularities may arise in unbounded domains, even when the small parameter only occurs in the minor derivatives (at infinity they play in a sense an equal, or even more major, role as the leading terms).
For example, consider a second-order elliptic partial differential equation in a bounded domain 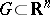 . The solution of the problem
. The solution of the problem
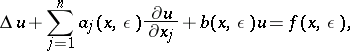 |
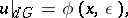 |
is a smooth function of  , for small
, for small  , if the boundary is smooth, if
, if the boundary is smooth, if 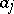 ,
, 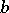 ,
, 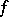 ,
, 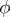 are smooth functions of
are smooth functions of  and
and  , and if the limit boundary value problem
, and if the limit boundary value problem
 |
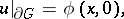 |
is uniquely solvable for any smooth functions 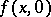 ,
, 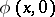 . The solution can be expanded in an asymptotic series in powers of
. The solution can be expanded in an asymptotic series in powers of  :
:
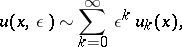 | (1) |
whose coefficients 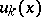 are solutions of the same type of boundary value problem and are easily calculated by perturbation theory.
are solutions of the same type of boundary value problem and are easily calculated by perturbation theory.
Quite a different situation holds, for example, for the boundary value problem
 | (2) |
since for 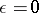 the order of the equation is less. The limit problem has the form
the order of the equation is less. The limit problem has the form
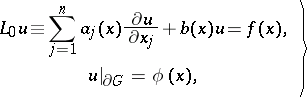 | (3) |
and, in general, is unsolvable. Let  , let the characteristics of the limit equation have the form depicted in the figure and let their orientation be induced by the vector field
, let the characteristics of the limit equation have the form depicted in the figure and let their orientation be induced by the vector field  .
.

Figure: s085820a
If the solution of the limit equation is known at some point, then it is known along all characteristics passing through the point; therefore the boundary value problem (3) is unsolvable for 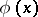 arbitrary. As
arbitrary. As 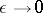 , the solution of (2) converges to a solution
, the solution of (2) converges to a solution 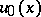 of the limit equation
of the limit equation 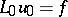 which is equal to
which is equal to 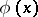 on the segments
on the segments 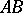 and
and 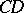 . On the remainder of the boundary the boundary conditions are lost. In a neighbourhood of each of the segments
. On the remainder of the boundary the boundary conditions are lost. In a neighbourhood of each of the segments  and
and 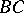 , having the typical width
, having the typical width 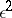 and called a boundary layer, the solution of (2) is close to the sum
and called a boundary layer, the solution of (2) is close to the sum
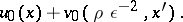 |
Here 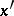 is the coordinate along the boundary
is the coordinate along the boundary 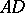 (
(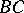 ),
), 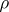 is the distance from the boundary along the normal, and
is the distance from the boundary along the normal, and 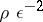 is the so-called inner variable. The solution of (2) expands as an asymptotic series of the form (1) everywhere except on the boundary layer and some special characteristic (in the figure, this is
is the so-called inner variable. The solution of (2) expands as an asymptotic series of the form (1) everywhere except on the boundary layer and some special characteristic (in the figure, this is 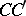 ). The partial sums of the asymptotic series uniformly approximate the solution of (2) in the domain obtained from
). The partial sums of the asymptotic series uniformly approximate the solution of (2) in the domain obtained from 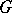 by removing fixed neighbourhoods of the lines
by removing fixed neighbourhoods of the lines 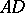 ,
, 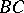 and
and 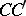 . In the boundary layer, outside a neighbourhood of the points
. In the boundary layer, outside a neighbourhood of the points 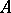 ,
, 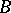 ,
, 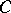 ,
, 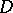 ,
,  , to the asymptotic series (1) one adds the asymptotic series
, to the asymptotic series (1) one adds the asymptotic series
 |
The functions 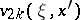 decrease exponentially as
decrease exponentially as 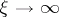 . The first asymptotic series is usually called the outer asymptotic series and the second the inner asymptotic series, and the functions
. The first asymptotic series is usually called the outer asymptotic series and the second the inner asymptotic series, and the functions 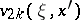 are called boundary-layer functions. This terminology, as even the problem itself, comes from the problem of fluid flow around bodies with small viscosity (see Hydrodynamics, mathematical problems in, and also [1]–[4]). This method is called the method of the boundary layer and is essentially the same as the method for ordinary differential equations.
are called boundary-layer functions. This terminology, as even the problem itself, comes from the problem of fluid flow around bodies with small viscosity (see Hydrodynamics, mathematical problems in, and also [1]–[4]). This method is called the method of the boundary layer and is essentially the same as the method for ordinary differential equations.
In neighbourhoods of the points 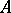 ,
, 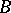 ,
, 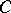 ,
, 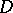 , at which the characteristics of
, at which the characteristics of 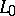 touch the boundary, and close to
touch the boundary, and close to 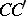 , the asymptotic behaviour of the solution is more complicated. The complications arise when the boundary is not everywhere smooth (has corners and, for
, the asymptotic behaviour of the solution is more complicated. The complications arise when the boundary is not everywhere smooth (has corners and, for 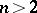 , edges). In some simple cases it is possible to construct asymptotic formulas by the addition of supplementary boundary-layer functions depending on more variables, but, as before, tending exponentially to zero at infinity. However, as a rule the picture is more complicated: both the coefficients
, edges). In some simple cases it is possible to construct asymptotic formulas by the addition of supplementary boundary-layer functions depending on more variables, but, as before, tending exponentially to zero at infinity. However, as a rule the picture is more complicated: both the coefficients 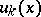 of the outer expansion and the coefficients
of the outer expansion and the coefficients  of the inner expansion have essential singularities at the singular points (
of the inner expansion have essential singularities at the singular points (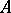 ,
, 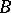 ,
, 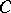 ,
, 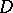 in the figure). The asymptotic expansion of the solution, uniformly in the closed domain
in the figure). The asymptotic expansion of the solution, uniformly in the closed domain  , can be constructed by the method of multiple scales (by the method of matched asymptotic series, [5]). Some problems for partial differential equations may be investigated by another variant of the method of multiple scales (the method of ascent): the solution is considered as a function of the basic independent variables and auxiliary "fast" variables. As a result the dimension of the original problem is increased but the dependence on the parameter is simplified (see [6]).
, can be constructed by the method of multiple scales (by the method of matched asymptotic series, [5]). Some problems for partial differential equations may be investigated by another variant of the method of multiple scales (the method of ascent): the solution is considered as a function of the basic independent variables and auxiliary "fast" variables. As a result the dimension of the original problem is increased but the dependence on the parameter is simplified (see [6]).
If the field of characteristics of the limit operator 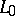 has stationary points, then the problem significantly complicates. For example, if
has stationary points, then the problem significantly complicates. For example, if 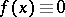 ,
, 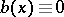 , and if all the characteristics are directed into the domain, then the solution of (2) tends to a constant as
, and if all the characteristics are directed into the domain, then the solution of (2) tends to a constant as 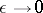 . Finding this constant and constructing an asymptotic series of the solution is a difficult, only partly solved problem (see [7]). Equation (2) describes random perturbations of the dynamical system
. Finding this constant and constructing an asymptotic series of the solution is a difficult, only partly solved problem (see [7]). Equation (2) describes random perturbations of the dynamical system 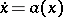 . Problems in this area were also at the origin of the development of the method of the small parameter in the theory of partial differential equations (see [8]).
. Problems in this area were also at the origin of the development of the method of the small parameter in the theory of partial differential equations (see [8]).
If 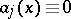 in (2) and
in (2) and 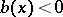 , then the asymptotic series is easily found; far from the boundary the series has the form (1) and in the boundary layer, close to the boundary, the asymptotic series
, then the asymptotic series is easily found; far from the boundary the series has the form (1) and in the boundary layer, close to the boundary, the asymptotic series
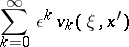 |
is added, where now 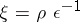 .
.
The problem is really complicated if 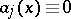 ,
, 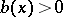 . In this case the solution strongly oscillates; the asymptotic methods are the WKB method; semi-classical approximation; the parabolic-equation method, etc.
. In this case the solution strongly oscillates; the asymptotic methods are the WKB method; semi-classical approximation; the parabolic-equation method, etc.
There is a class of problems in which the boundary of the domain degenerates as 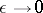 . For the sake of being specific, consider the problem
. For the sake of being specific, consider the problem
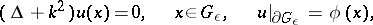 | (4) |
where 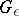 is the exterior of a bounded domain
is the exterior of a bounded domain 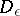 in
in 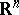 and
and  ; at infinity the radiation conditions are posed. For example, let
; at infinity the radiation conditions are posed. For example, let 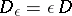 ,
, 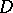 being a fixed domain containing
being a fixed domain containing 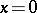 ; then
; then 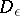 contracts to the point
contracts to the point 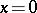 and (4) has no limit. The quantity
and (4) has no limit. The quantity 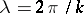 has the sense of wavelength: here
has the sense of wavelength: here  , where
, where 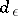 is the diameter of
is the diameter of 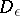 , and one speaks of dispersion of wavelengths on the obstacle
, and one speaks of dispersion of wavelengths on the obstacle 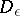 (or hydrodynamic approximation, or Rayleigh approximation). There are two overlapping zones: the nearer containing
(or hydrodynamic approximation, or Rayleigh approximation). There are two overlapping zones: the nearer containing 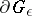 , with size tending to zero as
, with size tending to zero as 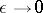 , and the farther, the exterior of the domain, contracting to the point
, and the farther, the exterior of the domain, contracting to the point  as
as 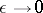 . The asymptotic series of the solution has different forms in these zones. The first boundary value problem for
. The asymptotic series of the solution has different forms in these zones. The first boundary value problem for 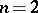 turns out to be the most difficult; the inner asymptotic expansion has the form
turns out to be the most difficult; the inner asymptotic expansion has the form
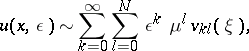 |
where  ,
, 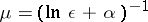 and
and 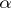 is a constant (see [9]). The long-wave approximation has been studied mainly for the Helmholtz equation and for the Maxwell system (see [10], [11]).
is a constant (see [9]). The long-wave approximation has been studied mainly for the Helmholtz equation and for the Maxwell system (see [10], [11]).
Another variant arises when 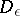 contracts to an interval
contracts to an interval 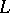 as
as 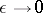 ; in this case there is a limit problem for
; in this case there is a limit problem for 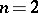 but not for
but not for 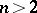 . Problems of this type (including those for the Laplace equation, for linear hyperbolic equations and for non-linear partial differential equations) arise in hydrodynamics and aerodynamics, in the theory of diffraction of waves (flow around a thin body of a fluid or a gas). The problem (4) has been investigated for
. Problems of this type (including those for the Laplace equation, for linear hyperbolic equations and for non-linear partial differential equations) arise in hydrodynamics and aerodynamics, in the theory of diffraction of waves (flow around a thin body of a fluid or a gas). The problem (4) has been investigated for 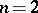 (see [12]); for
(see [12]); for 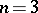 it has been investigated if
it has been investigated if 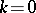 and
and 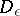 is a solid of revolution (see [13]).
is a solid of revolution (see [13]).
Partial differential equations containing a small parameter arise naturally in the study of non-linear oscillations when the perturbation has order  but the solution is studied over a large time interval of order
but the solution is studied over a large time interval of order 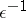 . If a continuous medium is considered instead of a system of particles, then partial differential equations arise to which generalizations of the averaging method apply (see [14]).
. If a continuous medium is considered instead of a system of particles, then partial differential equations arise to which generalizations of the averaging method apply (see [14]).
References
| [1] | H. Schlichting, "Boundary layer theory" , McGraw-Hill (1955) (Translated from German) |
| [2] | M. van Dyke, "Perturbation methods in fluid mechanics" , Parabolic Press (1975) |
| [3] | M.I. Vishik, L.A. Lyusternik, "Regular degeneracy and boundary layer for linear differential equations with a small parameter" Uspekhi Mat. Nauk , 12 : 5 (1957) pp. 3–122 (In Russian) |
| [4] | V.A. Trenogin, "The development and applications of the asymptotic method of Lyusternik and Vishik" Russian Math. Surveys , 25 : 4 (1970) pp. 119–156 Uspekhi Mat. Nauk , 25 : 4 (1970) pp. 123–156 |
| [5] | A.H. Nayfeh, "Perturbation methods" , Wiley (1973) |
| [6] | S.A. Lomov, "The method of perturbations for singular problems" Math. USSR-Izv. , 6 : 3 (1972) pp. 631–648 Izv. Akad. Nauk SSSR Ser. Mat. , 36 : 3 (1972) pp. 635–651 |
| [7] | L.D. Venttsel', "Random perturbations of dynamical systems" , Springer (1984) (Translated from Russian) |
| [8] | L.S. Pontryagin, A.A. Andronov, A.A. Vitt, Zh. Eksper. i Teoret. Fiz. , 3 : 3 (1933) pp. 165–180 |
| [9] | A.M. Il'in, "A boundary value problem for the second order elliptic equation in a domain with a narrow slit. 2. Domain with a small cavity" Math. USSR Sb. , 32 : 2 (1977) pp. 227–244 Mat. Sb. , 103 : 2 (1977) pp. 265–284 |
| [10] | A.W. Mane, "Theorie der Beugung" S. Flügge (ed.) , Handbuch der Physik , 25/1 , Springer (1961) pp. 218–573 |
| [11] | P.M. Morse, H. Feshbach, "Methods of theoretical physics" , 2 , McGraw-Hill (1953) |
| [12] | A.M. Il'in, "A boundary value problem for the elliptic equation of second order in a domain with a narrow slit. 1. The two-dimensional case" Math. USSR Sb. , 28 : 4 (1976) pp. 459–480 Mat. Sb. , 99 : 4 (1976) pp. 514–537 |
| [13] | J.D. Cole, "Perturbation methods in applied mathematics" , Blaisdell (1968) |
| [14] | Yu.A. Mitropol'skii, B.I. Moseenkov, "Asymptotic solutions of partial differential equations" , Kiev (1976) (In Russian) |
A.M. Il'inM.V. Fedoryuk
Comments
References [a1]–[a4] are selected from the large Western literature concerning the general subject of singular perturbations, i.e. (a particular kind of) singular small parameter equations; cf. also (the editorial comments headed "singular perturbations" in) Perturbation theory. Another interesting specific topic in the same area is the Hamilton–Jacobi equation, as a limit of parabolic equations with a small parameter [a5].
References
| [a1] | R.E. O'Malley, "Introduction to singular perturbations" , Acad. Press (1974) |
| [a2] | J. Kevorkian, J.D. Cole, "Perturbation methods in applied mathematics" , Springer (1981) |
| [a3] | J.D. Murray, "Asymptotic analysis" , Springer (1984) |
| [a4] | P.A. Lagerstrom, "Matched asymptotic expansions" , Springer (1988) |
| [a5] | D.G. Aronson, J.L. Vazquez, "The porous medium equation as a finite-speed approximation to a Hamiltonian–Jacobi equation" Ann. Inst. H. Poincaré Anal. Non Linéaire , 4 (1987) pp. 203–230 |
Small parameter, method of the. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Small_parameter,_method_of_the&oldid=18565