Difference between revisions of "Skew Young tableau"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | Consider two partitions, | + | {{TEX|done}} |
| + | Consider two partitions, $\lambda$ of $n+m$ and $\mu$ of $m$. With those partitions one can associate Young diagrams, or Ferrers diagrams (cf. [[Young diagram|Young diagram]]), also denoted by $\lambda$ and $\mu$. Suppose that each cell of $\mu$ is also a cell of $\lambda$. The set-difference $\lambda/\mu$ contains exactly $n$ cells. It is called a skew Young diagram, or skew Ferrers diagram. | ||
| − | Such a diagram can be filled with integers from | + | Such a diagram can be filled with integers from $1$ to $n$ in increasing order in each row and in each column. This is called a standard skew Young tableau. If repetitions are allowed and if the rows are only non-decreasing, the tableau is called semi-standard. These are generalizations of Young tableaux (cf. [[Young tableau|Young tableau]]). |
For example, | For example, | ||
| Line 9: | Line 10: | ||
Figure: s110150a | Figure: s110150a | ||
| − | are standard, respectively semi-standard, of shape | + | are standard, respectively semi-standard, of shape $(4,3,2)/(1,1)$. |
| − | It is possible to define the Schur function | + | It is possible to define the Schur function $S_\lambda(X)$ combinatorially as the generating function of all semi-standard Young tableaux of shape $\lambda$ filled with indices of elements of $X$, as follows. |
| − | Let | + | Let $X=\{x_1,\ldots,x_k\}$ be an alphabet. Let $T$ be a semi-standard Young tableau of shape $\lambda$, containing entries from $1$ to $k$. The product of the indeterminates whose indices appear in $T$ is a monomial. Then $S_\lambda(X)$ is the sum of those monomials over the set of all possible such tableaux $T$. |
| − | When replacing Young tableaux by skew Young tableaux of shape | + | When replacing Young tableaux by skew Young tableaux of shape $\lambda/\mu$, one obtains the skew Schur function $S_{\lambda/\mu}(X)$. Those functions have many properties in common with ordinary Schur functions. See [[#References|[a3]]] for Schur functions. |
| − | This connection between combinatorial (Young tableaux) and algebraic (Schur functions) objects is very fruitful, both for combinatorics and for algebra. For applications to | + | This connection between combinatorial (Young tableaux) and algebraic (Schur functions) objects is very fruitful, both for combinatorics and for algebra. For applications to $q$-analysis, cf., e.g., [[#References|[a1]]] and [[#References|[a2]]]. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Désarménien, "Fonctions symétriques associées à des suites classiques de nombres" ''Ann. Sci. Ecole Normale Sup.'' , '''16''' (1983) pp. 231–304</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Désarménien, D. Foata, "Fonctions symétriques et séries hypergéométriques basiques multivariées" ''Bull. Soc. Math. France'' , '''113''' (1985) pp. 3–22</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> I.G. Macdonald, "Symmetric functions and Hall polynomials" , Clarendon Press (1995) (Edition: Second)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Désarménien, "Fonctions symétriques associées à des suites classiques de nombres" ''Ann. Sci. Ecole Normale Sup.'' , '''16''' (1983) pp. 231–304</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Désarménien, D. Foata, "Fonctions symétriques et séries hypergéométriques basiques multivariées" ''Bull. Soc. Math. France'' , '''113''' (1985) pp. 3–22</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> I.G. Macdonald, "Symmetric functions and Hall polynomials" , Clarendon Press (1995) (Edition: Second)</TD></TR></table> | ||
Revision as of 15:02, 30 July 2014
Consider two partitions, $\lambda$ of $n+m$ and $\mu$ of $m$. With those partitions one can associate Young diagrams, or Ferrers diagrams (cf. Young diagram), also denoted by $\lambda$ and $\mu$. Suppose that each cell of $\mu$ is also a cell of $\lambda$. The set-difference $\lambda/\mu$ contains exactly $n$ cells. It is called a skew Young diagram, or skew Ferrers diagram.
Such a diagram can be filled with integers from $1$ to $n$ in increasing order in each row and in each column. This is called a standard skew Young tableau. If repetitions are allowed and if the rows are only non-decreasing, the tableau is called semi-standard. These are generalizations of Young tableaux (cf. Young tableau).
For example,
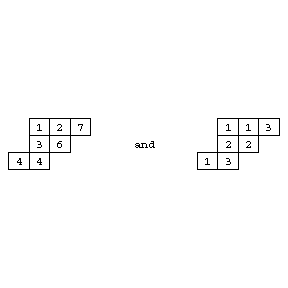
Figure: s110150a
are standard, respectively semi-standard, of shape $(4,3,2)/(1,1)$.
It is possible to define the Schur function $S_\lambda(X)$ combinatorially as the generating function of all semi-standard Young tableaux of shape $\lambda$ filled with indices of elements of $X$, as follows.
Let $X=\{x_1,\ldots,x_k\}$ be an alphabet. Let $T$ be a semi-standard Young tableau of shape $\lambda$, containing entries from $1$ to $k$. The product of the indeterminates whose indices appear in $T$ is a monomial. Then $S_\lambda(X)$ is the sum of those monomials over the set of all possible such tableaux $T$.
When replacing Young tableaux by skew Young tableaux of shape $\lambda/\mu$, one obtains the skew Schur function $S_{\lambda/\mu}(X)$. Those functions have many properties in common with ordinary Schur functions. See [a3] for Schur functions.
This connection between combinatorial (Young tableaux) and algebraic (Schur functions) objects is very fruitful, both for combinatorics and for algebra. For applications to $q$-analysis, cf., e.g., [a1] and [a2].
References
| [a1] | J. Désarménien, "Fonctions symétriques associées à des suites classiques de nombres" Ann. Sci. Ecole Normale Sup. , 16 (1983) pp. 231–304 |
| [a2] | J. Désarménien, D. Foata, "Fonctions symétriques et séries hypergéométriques basiques multivariées" Bull. Soc. Math. France , 113 (1985) pp. 3–22 |
| [a3] | I.G. Macdonald, "Symmetric functions and Hall polynomials" , Clarendon Press (1995) (Edition: Second) |
Skew Young tableau. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Skew_Young_tableau&oldid=14010