Skew-field
A ring in which the equations  and
and 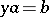 with
with 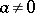 are uniquely solvable. In the case of an associative ring (cf. Associative rings and algebras) it is sufficient to require the existence of a unit 1 and the unique solvability of the equations
are uniquely solvable. In the case of an associative ring (cf. Associative rings and algebras) it is sufficient to require the existence of a unit 1 and the unique solvability of the equations 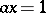 and
and 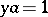 for any
for any 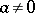 . A commutative associative skew-field is called a field. An example of a non-commutative associative skew-field is the skew-field of quaternions, defined as the set of matrices of the form
. A commutative associative skew-field is called a field. An example of a non-commutative associative skew-field is the skew-field of quaternions, defined as the set of matrices of the form
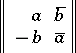 |
over the field of complex numbers with the usual operations (see Quaternion). An example of a non-associative skew-field is the Cayley–Dickson algebra, consisting of all matrices of the same form as above over the skew-field of quaternions. This skew-field is alternative (see Alternative rings and algebras). Any skew-field is a division algebra either over the field of rational numbers or over a field of residues 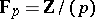 . The skew-field of quaternions is a
. The skew-field of quaternions is a 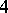 -dimensional algebra over the field of real numbers, while the Cayley–Dickson algebra is
-dimensional algebra over the field of real numbers, while the Cayley–Dickson algebra is 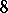 -dimensional. The dimension of any algebra with division over the field of real numbers is equal to 1, 2, 4, or 8 (see [1], and also Topological ring). The fields of real or complex numbers and the skew-field of quaternions are the only connected locally compact associative skew-fields (see [5]). Any finite-dimensional algebra without zero divisors is a skew-field. Any finite associative skew-field is commutative (see [6], [8]). An associative skew-field is characterized by the property that any non-zero module over it is free. Any non-associative skew-field is finite-dimensional [3]. A similar result applies to Mal'tsev skew-fields [7] (see Mal'tsev algebra) and to Jordan skew-fields [4] (see Jordan algebra). In contrast to the commutative case, not every associative ring without zero divisors can be imbedded in a skew-field (see Imbedding of rings).
-dimensional. The dimension of any algebra with division over the field of real numbers is equal to 1, 2, 4, or 8 (see [1], and also Topological ring). The fields of real or complex numbers and the skew-field of quaternions are the only connected locally compact associative skew-fields (see [5]). Any finite-dimensional algebra without zero divisors is a skew-field. Any finite associative skew-field is commutative (see [6], [8]). An associative skew-field is characterized by the property that any non-zero module over it is free. Any non-associative skew-field is finite-dimensional [3]. A similar result applies to Mal'tsev skew-fields [7] (see Mal'tsev algebra) and to Jordan skew-fields [4] (see Jordan algebra). In contrast to the commutative case, not every associative ring without zero divisors can be imbedded in a skew-field (see Imbedding of rings).
References
| [1] | J.F. Adams, "On the nonexistence of elements of Hopf invariant one" Bulletin Amer. Math. Soc. , 64 : 5 (1958) pp. 279–282 |
| [2] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [3] | K.A. Zhevlakov, A.M. Slin'ko, I.P. Shestakov, A.I. Shirshov, "Rings that are nearly associative" , Acad. Press (1982) (Translated from Russian) |
| [4] | E.I. Zel'manov, "Jordan division algebras" Algebra and Logic , 18 : 3 (1979) pp. 175–190 Algebra i Logika , 18 : 3 (1979) pp. 286–310 |
| [5] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [6] | L.A. Skornyakov, "Elements of general algebra" , Moscow (1983) (In Russian) |
| [7] | V.T. Filippov, "Central simple Mal'tsev algebras" Algebra and Logic , 15 : 2 (1976) pp. 147–151 Algebra i Logika , 15 : 2 (1976) pp. 235–242 |
| [8] | I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968) |
Comments
Associative skew-fields are also known as division rings, in particular if they are finite dimensional over their centre. For the imbedding problem see [a1].
The theorem that the only associative division algebras over 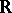 are
are 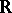 ,
,  or
or  , the algebra of quaternions, is known as Frobenius' theorem.
, the algebra of quaternions, is known as Frobenius' theorem.
References
| [a1] | P.M. Cohn, "Skew field constructions" , Cambridge Univ. Press (1977) |
| [a2] | P.M. Cohn, "Algebra" , 3 , Wiley (1991) pp. Chapt. 7 |
Skew-field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Skew-field&oldid=21398