Difference between revisions of "Singularities of differentiable mappings"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | s0856201.png | ||
| + | $#A+1 = 312 n = 7 | ||
| + | $#C+1 = 312 : ~/encyclopedia/old_files/data/S085/S.0805620 Singularities of differentiable mappings | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A branch of mathematical analysis and differential geometry, in which those properties of mappings are studied which are preserved when the coordinates in the image and pre-image of the mapping are changed (or when changes are made which preserve certain supplementary structures); a general approach is proposed to the solution of various problems on degeneration of mappings, functions, vector fields, etc.; a classification is given of the most commonly encountered degenerations, and their normal forms, as well as algorithms which reduce to the normal forms, are determined. | A branch of mathematical analysis and differential geometry, in which those properties of mappings are studied which are preserved when the coordinates in the image and pre-image of the mapping are changed (or when changes are made which preserve certain supplementary structures); a general approach is proposed to the solution of various problems on degeneration of mappings, functions, vector fields, etc.; a classification is given of the most commonly encountered degenerations, and their normal forms, as well as algorithms which reduce to the normal forms, are determined. | ||
| − | A point of the domain of definition of a differentiable mapping (i.e. a mapping of class | + | A point of the domain of definition of a differentiable mapping (i.e. a mapping of class $ C ^ {k} $, |
| + | see [[Differentiable manifold|Differentiable manifold]]) is said to be regular if the Jacobi matrix has maximum rank at this point, and critical in the opposite case. | ||
The classical [[Implicit function|implicit function]] theorem describes the structure of a mapping in a neighbourhood of a regular point; in a neighbourhood of this point and in a neighbourhood of its image, there exist coordinates in which the mapping is linear. | The classical [[Implicit function|implicit function]] theorem describes the structure of a mapping in a neighbourhood of a regular point; in a neighbourhood of this point and in a neighbourhood of its image, there exist coordinates in which the mapping is linear. | ||
| Line 25: | Line 38: | ||
The choice of the set of typical mappings depends on the problem to be solved and is not unique: the fewer the mappings that are typical, the easier they are to study, although 2) and 3) require that the set of typical mappings is sufficiently broad and sufficiently constructively defined. | The choice of the set of typical mappings depends on the problem to be solved and is not unique: the fewer the mappings that are typical, the easier they are to study, although 2) and 3) require that the set of typical mappings is sufficiently broad and sufficiently constructively defined. | ||
| − | This scheme is illustrated by the Whitney theorem: Every differentiable mapping | + | This scheme is illustrated by the Whitney theorem: Every differentiable mapping $ \mathbf R ^ {2} \rightarrow \mathbf R ^ {2} $ |
| + | can be approximated by a mapping $ f $ | ||
| + | such that for any point $ a \in \mathbf R ^ {2} $ | ||
| + | in neighbourhoods of $ a $ | ||
| + | and $ f( a) $ | ||
| + | coordinates can be chosen at which the mapping $ f $ | ||
| + | has one of the three normal forms: | ||
| − | + | $$ | |
| + | \left \{ \begin{array}{l} | ||
| + | y _ {1} = x _ {1} , \\ | ||
| + | y _ {2} = x _ {2} ; | ||
| + | \end{array} | ||
| + | \right . \ \ | ||
| + | \left \{ \begin{array}{l} | ||
| + | y _ {1} = x _ {1} , \\ | ||
| + | y _ {2} = x _ {2} ^ {2} ; | ||
| + | \end{array} | ||
| + | \right . \ \ | ||
| + | \left \{ \begin{array}{l} | ||
| + | y _ {1} = x _ {1} , \\ | ||
| + | y _ {2} = x _ {2} ^ {3} + x _ {1} x _ {2} | ||
| + | \end{array} | ||
| + | \right . | ||
| + | $$ | ||
(for the typicality criterion, see [[#References|[3]]], [[#References|[4]]]). The work of H. Whitney (1955), in which this theorem was proved, is considered to be the beginning of the theory of singularities of differentiable mappings, although a number of individual results appeared far earlier ([[Morse theory|Morse theory]] of critical points of functions, Whitney's theorem on singularities of imbeddings, the work of L.S. Pontryagin on the connection between singularities and characteristic classes). | (for the typicality criterion, see [[#References|[3]]], [[#References|[4]]]). The work of H. Whitney (1955), in which this theorem was proved, is considered to be the beginning of the theory of singularities of differentiable mappings, although a number of individual results appeared far earlier ([[Morse theory|Morse theory]] of critical points of functions, Whitney's theorem on singularities of imbeddings, the work of L.S. Pontryagin on the connection between singularities and characteristic classes). | ||
==Basic concepts in the theory of singularities of differentiable mappings.== | ==Basic concepts in the theory of singularities of differentiable mappings.== | ||
| − | |||
===Germs of differentiable mappings.=== | ===Germs of differentiable mappings.=== | ||
| − | Let | + | Let $ X $ |
| + | and $ Y $ | ||
| + | be smooth manifolds, $ p \in X $, | ||
| + | $ q \in Y $. | ||
| + | (Hereafter, the term "smooth" will be used as a synonym for infinitely differentiable.) An equivalence class of mappings $ X \rightarrow Y $ | ||
| + | which coincide in a certain neighbourhood of the point $ p $ | ||
| + | is called a germ at the point $ p $; | ||
| + | the set of germs of mappings which transfer $ p $ | ||
| + | to $ q $ | ||
| + | is denoted by $ C ^ \infty ( X, Y) _ {p,q} $. | ||
| + | The group of germs of smooth changes of variables in $ X $ | ||
| + | which preserve the point $ p $ | ||
| + | is denoted by $ \mathop{\rm Diff} ^ \infty ( X) _ {p} $. | ||
An important local problem in the theory of singularities of differentiable mappings is the study of the natural action of the group | An important local problem in the theory of singularities of differentiable mappings is the study of the natural action of the group | ||
| − | + | $$ | |
| + | \mathop{\rm Diff} ^ \infty ( X) _ {p} \times \mathop{\rm Diff} ^ \infty ( Y) _ {q} \ \ | ||
| + | \mathop{\rm on} C ^ \infty ( X, Y) _ {p,q} . | ||
| + | $$ | ||
The solution of this and many similar problems is usually begun by approximating the function spaces and the infinite-dimensional groups acting on them by finite-dimensional manifolds and the actions on them by Lie groups. The results obtained are then transferred to the initial infinite-dimensional situation. | The solution of this and many similar problems is usually begun by approximating the function spaces and the infinite-dimensional groups acting on them by finite-dimensional manifolds and the actions on them by Lie groups. The results obtained are then transferred to the initial infinite-dimensional situation. | ||
===Jet bundles.=== | ===Jet bundles.=== | ||
| − | Let | + | Let $ f, g: X \rightarrow Y $ |
| + | be smooth mappings, and let $ f( p) = g( p) = q $; | ||
| + | the mappings $ f $ | ||
| + | and $ g $ | ||
| + | have, by definition, contact of order $ k $ | ||
| + | at the point $ p $ | ||
| + | if their [[Taylor series|Taylor series]] at this point coincide up to the order $ k $. | ||
| + | An equivalence class of mappings which have contact of order $ k $ | ||
| + | at the point $ p $ | ||
| + | is called a $ k $- | ||
| + | jet. The set of all $ k $- | ||
| + | jets of mappings which transfer $ p $ | ||
| + | to $ q $ | ||
| + | has the natural structure of a smooth manifold and is denoted by $ J ^ {k} ( X, Y) _ {p,q} $. | ||
| + | There is a well-defined natural projection | ||
| − | + | $$ | |
| + | C ^ \infty ( X, Y) _ {p,q} \rightarrow J ^ {k} ( X, Y) _ {p,q} . | ||
| + | $$ | ||
| − | The equivalence class of smooth changes of variables in | + | The equivalence class of smooth changes of variables in $ X $ |
| + | which preserve the point $ p $ | ||
| + | and have contact of order $ k $ | ||
| + | at this point is called an invertible $ k $- | ||
| + | jet at $ p $. | ||
| + | The invertible $ k $- | ||
| + | jets form a Lie group $ L ^ {k} ( X) _ {p} $. | ||
| + | The Lie group $ L ^ {k} ( X) _ {p} \times L ^ {k} ( Y) _ {q} $ | ||
| + | acts on $ J ^ {k} ( X, Y) _ {p,q} $ | ||
| + | and approximates the action of | ||
| − | + | $$ | |
| + | \mathop{\rm Diff} ^ \infty ( X) _ {p} \times \mathop{\rm Diff} ^ \infty ( Y) _ {q} \ \ | ||
| + | \mathop{\rm on} C ^ \infty ( X, Y) _ {p,q} . | ||
| + | $$ | ||
| − | Let | + | Let $ J ^ {k} ( X, Y) = \{ \textrm{ disjoint union of } J ^ {k} ( X, Y) _ {p,q } \textrm{ over { } all } ( p, q) \in X \times Y \} $. |
| + | The set $ J ^ {k} ( X, Y) $ | ||
| + | has the natural structure of a smooth bundle over $ X \times Y $ | ||
| + | with fibre | ||
| − | + | $$ | |
| + | J ^ {k} ( \mathbf R ^ {m} , \mathbf R ^ {n} ) _ {0,0} = J ^ {k} ( m, n) | ||
| + | $$ | ||
and structure group | and structure group | ||
| − | + | $$ | |
| + | L ^ {k} ( \mathbf R ^ {m} ) _ {0} \times L ^ {k} ( \mathbf R ^ {n} ) _ {0} = \ | ||
| + | L ^ {k} ( m, n), | ||
| + | $$ | ||
| − | where | + | where $ m = \mathop{\rm dim} X $, |
| + | $ n = \mathop{\rm dim} Y $. | ||
===Singularities and classes of singularities.=== | ===Singularities and classes of singularities.=== | ||
| − | An orbit of the action of | + | An orbit of the action of $ L ^ {k} ( m, n) $ |
| + | on $ J ^ {k} ( m, n) $ | ||
| + | is called a $ k $- | ||
| + | singularity; any subset in $ J ^ {k} ( m, n) $ | ||
| + | that is invariant under $ L ^ {k} ( m, n) $ | ||
| + | is called a class of $ k $- | ||
| + | singularities. Let $ S $ | ||
| + | be such a class. Because $ J ^ {k} ( m, n) $ | ||
| + | can be identified with $ J ^ {k} ( X, Y) _ {p,q} $, | ||
| + | the subset $ S( X, Y) _ {p,q} $ | ||
| + | is defined in $ J ^ {k} ( X, Y) _ {p,q} $, | ||
| + | irrespective of the method of identification. The set $ S( X, Y) = \{ \textrm{ union of } S( X, Y) _ {p,q} \textrm{ over { } all } ( p, q) \in X \times Y \} $ | ||
| + | is called a universal class of singularities (or a universal singularity if $ S $ | ||
| + | is a singularity). A universal singularity $ S( X, Y) $ | ||
| + | is a submanifold in $ J ^ {k} ( X, Y) $ | ||
| + | of codimension equal to the codimension of $ S $ | ||
| + | in $ J ^ {k} ( m, n) $. | ||
| − | Let | + | Let $ F: X \rightarrow Y $ |
| + | be a smooth mapping. The smooth mapping $ j ^ {k} f: X \rightarrow J ^ {k} ( X, Y) $, | ||
| + | called the $ k $- | ||
| + | jet extension of $ f $, | ||
| + | is obtained by assigning to each point $ p \in X $ | ||
| + | the $ k $- | ||
| + | jet of $ f $ | ||
| + | at $ p $. | ||
| + | The mapping $ f: X \rightarrow Y $ | ||
| + | has, by definition, a singularity of type $ S $ | ||
| + | at the point $ p $ | ||
| + | if $ j ^ {k} f( p) \in S( X, Y) $. | ||
| + | The set $ S( f ) $ | ||
| + | of all points at which $ f $ | ||
| + | has a singularity of type $ S $ | ||
| + | is none other than $ ( j ^ {k} f ) ^ {-} 1 S( X, Y) $. | ||
| + | The study of the set $ S( f ) $ | ||
| + | thus divides into two stages: the study of the universal set $ S( X, Y) $ | ||
| + | in $ J ^ {k} ( X, Y) $, | ||
| + | which reduces to the study of $ S $ | ||
| + | in $ J ^ {k} ( m, n) $, | ||
| + | and the study of the mutual positions of $ S( X, Y) $ | ||
| + | and $ j ^ {k} f( X) $. | ||
| + | In the second stage one usually employs Thom's transversality theorem. | ||
===Transversality.=== | ===Transversality.=== | ||
| − | A smooth mapping | + | A smooth mapping $ f: A\rightarrow B $ |
| + | of smooth manifolds is transversal to a submanifold $ C \subset B $( | ||
| + | denoted $ f \perp C $) | ||
| + | if for any point $ a \in A $ | ||
| + | either $ f( a) \notin C $ | ||
| + | or $ ( df ) _ {a} ( T _ {a} A) \oplus T _ {f(} a) C = T _ {f(} a) B $. | ||
| + | If $ f \perp C $, | ||
| + | then the set $ f ^ { - 1 } ( C) $ | ||
| + | is either empty or is a submanifold in $ A $ | ||
| + | of codimension equal to the codimension of $ C $ | ||
| + | in $ B $. | ||
| − | Thom's transversality theorem: Let | + | Thom's transversality theorem: Let $ X, Y $ |
| + | be smooth manifolds and let $ C $ | ||
| + | be a submanifold in $ J ^ {k} ( X, Y) $; | ||
| + | then the set of those $ f $ | ||
| + | for which $ j ^ {k} f \perp C $ | ||
| + | is a massive subset in $ C ^ \infty ( X, Y) $ | ||
| + | in the Whitney $ C ^ \infty $- | ||
| + | topology. (A set is said to be massive (generic) if it is the intersection of a countable number of open dense subsets. A property is called generic if it holds for all $ f $ | ||
| + | in a generic subset.) | ||
| − | The Whitney topology. Let | + | The Whitney topology. Let $ k \geq 0 $ |
| + | and let $ U $ | ||
| + | be an open set in $ J ^ {k} ( X, Y) $. | ||
| + | Let | ||
| − | + | $$ | |
| + | M( U) = \{ {f \in C ^ \infty ( X, Y) } : {j ^ {k} f( X) \subset U } \} | ||
| + | . | ||
| + | $$ | ||
| − | The sets | + | The sets $ M( U) $ |
| + | form the basis of some topology, called the Whitney $ C ^ \infty $- | ||
| + | topology, on $ C ^ \infty ( X, Y) $. | ||
| + | In this topology, $ C ^ \infty ( X, Y) $ | ||
| + | is a [[Baire space|Baire space]], i.e. every massive subset is dense. | ||
===Multi-jets.=== | ===Multi-jets.=== | ||
| − | In the study of the self-intersection of the image of a smooth mapping, the concept of a multi-jet is used. Let | + | In the study of the self-intersection of the image of a smooth mapping, the concept of a multi-jet is used. Let $ \alpha : J ^ {k} ( X, Y) \rightarrow X $ |
| + | be the natural projection. Let | ||
| − | + | $$ | |
| + | X ^ {(} s) = \{ {( x _ {1} \dots x _ {s} ) \in X \times \dots \times X } : { | ||
| + | x _ {j} \neq x _ {i} , i \neq j } \} | ||
| + | $$ | ||
| − | and let | + | and let $ \alpha ^ {s} = \alpha \times \dots \times \alpha $( |
| + | $ s $ | ||
| + | times). The set $ J _ {s} ^ {k} ( X, Y) = ( \alpha ^ {s} ) ^ {-} 1 ( X ^ {(} s) ) $ | ||
| + | may be given the natural structure of a smooth manifold and is called an $ s $- | ||
| + | fold bundle of $ k $- | ||
| + | jets. For $ s $- | ||
| + | fold jets, the $ k $- | ||
| + | jet extension of a mapping $ f $, | ||
| + | $ k $- | ||
| + | singularities, universal singularities, etc., are defined, and the analogue of Thom's transversality theorem has been proved. | ||
===Stable differentiable mappings.=== | ===Stable differentiable mappings.=== | ||
A central problem in the early days of the theory of singularities of differentiable mappings was the study of stable differentiable mappings. | A central problem in the early days of the theory of singularities of differentiable mappings was the study of stable differentiable mappings. | ||
| − | A smooth mapping | + | A smooth mapping $ f: X ^ {m} \rightarrow Y ^ {n} $ |
| + | of smooth manifolds is said to be stable if for any mapping $ \widetilde{f} $ | ||
| + | that is sufficiently close to $ f $ | ||
| + | there exists diffeomorphisms $ h: X ^ {m} \rightarrow X ^ {m} $ | ||
| + | and $ k: Y ^ {n} \rightarrow Y ^ {n} $ | ||
| + | such that $ \widetilde{f} = h \circ f \circ k $. | ||
| − | For small | + | For small $ m, n $( |
| + | $ m, n \leq 4 $), | ||
| + | as well as for $ n= 1 $ | ||
| + | and any $ m $, | ||
| + | stable differentiable mappings are dense in the space of all proper differentiable mappings [[#References|[3]]]. In the space of mappings $ X ^ {9} \rightarrow Y ^ {9} $, | ||
| + | stable mappings do not form an everywhere-dense set (see [[#References|[1]]]). For certain pairs of manifolds (for example, for $ X = \mathbf R P ^ {19} $, | ||
| + | $ Y = \mathbf R ^ {19} $) | ||
| + | there is no stable mapping from $ X $ | ||
| + | into $ Y $. | ||
| + | All "stable dimensions" $ ( m, n) $ | ||
| + | have been found in [[#References|[14]]], : For any smooth manifolds $ X ^ {m} $ | ||
| + | and $ Y ^ {n} $, | ||
| + | the stable mappings from $ X ^ {m} $ | ||
| + | into $ Y ^ {n} $ | ||
| + | are dense in the space of proper differentiable mappings $ X ^ {m} \rightarrow Y ^ {n} $, | ||
| + | equipped with the Whitney $ C ^ \infty $- | ||
| + | topology, if and only if the pair $ ( m, n) $ | ||
| + | satisfies at least one of the following conditions $ ( q = n- m) $: | ||
| + | a) $ n < 7q + 8 $ | ||
| + | and $ q \geq 4 $; | ||
| + | b) $ n < 7q + 9 $ | ||
| + | and $ 3 \geq q \geq 0 $; | ||
| + | c) $ n < 8 $ | ||
| + | and $ q = - 1 $; | ||
| + | d) $ n < 6 $ | ||
| + | and $ q = - 2 $; | ||
| + | e) $ n < 7 $ | ||
| + | and $ q \leq 3 $. | ||
| − | In proving this theorem, as well as in many other questions, the following two concepts prove to be useful: A mapping | + | In proving this theorem, as well as in many other questions, the following two concepts prove to be useful: A mapping $ f _ {0} : X ^ {m} \rightarrow Y ^ {n} $ |
| + | is called homotopy stable if for any smooth homotopy $ f _ {t} $ | ||
| + | of the mapping $ f _ {0} $ | ||
| + | there are smooth homotopies $ h _ {t} $ | ||
| + | and $ k _ {t} $ | ||
| + | of the identity diffeomorphisms of $ X ^ {m} $ | ||
| + | and $ Y ^ {n} $ | ||
| + | such that $ f _ {t} = h _ {t} \circ f _ {0} \circ k _ {t} $ | ||
| + | for sufficiently small $ t $. | ||
| + | A mapping $ f: X ^ {m} \rightarrow Y ^ {n} $ | ||
| + | is called infinitesimal stable if every mapping $ \widetilde{f} $ | ||
| + | that is infinitely close to $ f _ {0} $ | ||
| + | can be obtained from $ f _ {0} $ | ||
| + | by diffeomorphisms of $ X ^ {m} $ | ||
| + | and $ Y ^ {n} $ | ||
| + | which are "infinitely close to the identity" . For a proper mapping, the concepts of stability, homotopy stability and infinitesimal stability coincide [[#References|[3]]]. The problem of finding local normal forms of stable mappings reduces to the problem of classifying certain finite-dimensional local algebras [[#References|[14]]], . For fixed $ m, n $, | ||
| + | the number of such normal forms is finite. | ||
| − | If in the definition of a stable mapping, homeomorphisms | + | If in the definition of a stable mapping, homeomorphisms $ h $ |
| + | and $ k $ | ||
| + | are taken instead of diffeomorphisms, then the definition of a topologically stable mapping is obtained. The theorem on the density of the set of topological stable mappings in the set of all mappings of any compact manifold $ X ^ {m} $ | ||
| + | into any manifold $ Y ^ {n} $( | ||
| + | for any $ m, n $) | ||
| + | has been proved (see [[#References|[8]]]). | ||
===Finitely defined germs.=== | ===Finitely defined germs.=== | ||
| − | Let | + | Let $ \sim $ |
| + | be some equivalence relation on the set $ C ^ \infty ( \mathbf R ^ {m} , \mathbf R ^ {n} ) _ {0,0} $ | ||
| + | of germs of mappings $ \mathbf R ^ {m} \rightarrow \mathbf R ^ {n} $ | ||
| + | which take $ 0 $ | ||
| + | to $ 0 $. | ||
| + | The $ k $- | ||
| + | jet of any such germ is the segment of order $ k $ | ||
| + | of its Taylor series. A germ $ f $ | ||
| + | is said to be $ k $- | ||
| + | defined if any other germ $ g $ | ||
| + | with the same $ k $- | ||
| + | jet satisfies the relation $ f \sim g $. | ||
| + | A germ is finitely defined if it is $ k $- | ||
| + | defined for a certain $ k $. | ||
| + | A $ k $- | ||
| + | jet $ \sigma $ | ||
| + | such that any two germs $ f, g $ | ||
| + | which have $ \sigma $ | ||
| + | as $ k $- | ||
| + | jet satisfy the relation $ f \sim g $, | ||
| + | is said to be sufficient. The most commonly encountered equivalences have special names: | ||
| − | + | $ r $- | |
| + | equivalence — belonging to one orbit of the group $ \mathop{\rm Diff} ^ \infty ( \mathbf R ^ {m} ) _ {0} $ | ||
| + | of "correct" changes of coordinates. | ||
| − | + | $ rl $- | |
| + | equivalence — belonging to one orbit of the group $ \mathop{\rm Diff} ^ \infty ( \mathbf R ^ {m} ) _ {0} \times \mathop{\rm Diff} ^ \infty ( \mathbf R ^ {n} ) _ {0} $. | ||
| − | Topological equivalence — belonging to one orbit of the group | + | Topological equivalence — belonging to one orbit of the group $ \mathop{\rm Diff} ^ {0} ( \mathbf R ^ {m} ) _ {0} \times \mathop{\rm Diff} ^ {0} ( \mathbf R ^ {n} ) _ {0} $. |
| − | The study of | + | The study of $ k $- |
| + | defined germs reduces to the study of mappings defined by polynomials of degree $ \leq k $. | ||
| − | The question of whether a germ is | + | The question of whether a germ is $ k $- |
| + | defined with respect to $ rl $- | ||
| + | equivalence reduces to the problem of the solvability of an explicit system of finitely many linear equations. | ||
| − | The set of finitely defined germs with respect to | + | The set of finitely defined germs with respect to $ rl $- |
| + | equivalence is open in $ C ^ \infty ( \mathbf R ^ {m} , \mathbf R ^ {n} ) _ {0,0} $, | ||
| + | but is not dense for any $ m, n $. | ||
| + | It is natural to consider the coarser relation of topological equivalence. After rejection of a subset of finite codimension from $ C ^ \infty ( \mathbf R ^ {m} , \mathbf R ^ {n} ) _ {0,0} $, | ||
| + | a countable number of topological equivalence classes remains, each of which is a semi-algebraic set. It follows that the mappings with germs that are topologically equivalent to polynomial ones form an open dense set in $ C ^ \infty ( X, Y) $( | ||
| + | $ X ^ {m} $ | ||
| + | is compact) . | ||
===Deformation.=== | ===Deformation.=== | ||
| Line 120: | Line 371: | ||
===Classification.=== | ===Classification.=== | ||
| − | It is natural to begin by classifying the germs at 0 of holomorphic functions in | + | It is natural to begin by classifying the germs at 0 of holomorphic functions in $ \mathbf C ^ {n} $, |
| + | taking two germs to be equivalent if one can be transferred into the other by the germ of a holomorphic change of coordinates in $ \mathbf C ^ {n} $ | ||
| + | which preserves 0. A jet (Taylor polynomial) of a holomorphic function at 0 is sufficient if it defines the function up to equivalence. A germ whose critical point 0 is isolated always has a sufficient jet and, consequently, is equivalent to a polynomial. The number of non-degenerate critical points into which the critical point 0 splits when the function is shifted slightly is called the multiplicity (or Milnor number) $ \mu $ | ||
| + | of the critical point 0. If the multiplicity of a critical point of a function $ f $ | ||
| + | is equal to $ \mu $, | ||
| + | then the $ ( \mu + 1) $- | ||
| + | jet is sufficient. Since the multiplicity $ \mu $ | ||
| + | cannot increase under a small change of $ f $, | ||
| + | the classification of functions close to a function with an isolated critical point reduces to the study of the action of the Lie group of $ k $- | ||
| + | jets of changes of variables on the space of $ k $- | ||
| + | jets for a sufficiently large $ k $. | ||
| + | In a space of $ k $- | ||
| + | jets of functions $ f $ | ||
| + | for which $ f( 0) = 0 $, | ||
| + | $ df( 0) = 0 $, | ||
| + | the codimension of the orbit of $ f $ | ||
| + | is equal to $ \mu - 1 $; | ||
| + | thus, the critical points of multiplicity $ \mu $ | ||
| + | are non-removable in families of functions which depend on $ ( \mu - 1) $ | ||
| + | parameters. A classification (see [[#References|[10]]]) of all critical points of multiplicity $ \mu \leq 16 $ | ||
| + | and an algorithm for reducing any such function to a normal form have been obtained. The complexity of a critical point is defined not only by its multiplicity $ \mu $, | ||
| + | but also by its modality $ m $( | ||
| + | the number of moduli). A critical point is simple (or $ 0 $- | ||
| + | modal) if among the critical points near to it there are at most finitely many pairwise non-equivalent points. Two germs of functions are called stably equivalent if they become equivalent after being added directly to non-degenerate quadratic forms in the appropriate number of variables (for germs of functions in the same number of variables, stable equivalence is the same ordinary equivalence). | ||
Simple germs are exhausted up to stable equivalence by the following list: | Simple germs are exhausted up to stable equivalence by the following list: | ||
| − | + | $ A _ {k} $: | |
| + | $ f( x) = x ^ {k+} 1 $, | ||
| + | $ k \geq 1 $; | ||
| − | + | $ D _ {k} $: | |
| + | $ f( x, y) = x ^ {2} y + y ^ {k-} 1 $, | ||
| + | $ k \geq 4 $; | ||
| − | + | $ E _ {6} $: | |
| + | $ f( x, y) = x ^ {3} + y ^ {4} $; | ||
| − | + | $ E _ {7} $: | |
| + | $ f( x, y) = x ^ {3} + xy ^ {3} $; | ||
| − | + | $ E _ {8} $: | |
| + | $ f( x, y) = x ^ {3} + y ^ {5} $. | ||
| − | The modality of a point | + | The modality of a point $ x \in X $ |
| + | under the action of a Lie group $ G $ | ||
| + | on a manifold $ X $ | ||
| + | is the smallest number $ m $ | ||
| + | such that a sufficiently small neighbourhood of $ x $ | ||
| + | is covered by a finite number of $ m $- | ||
| + | parametric families of orbits. | ||
| − | A classification of germs of functions of modality 1 and 2 has also been obtained (see [[#References|[10]]]). The classification of simple singularities and singularities of small modality is related to Lie groups, the Coxeter and Weyl series | + | A classification of germs of functions of modality 1 and 2 has also been obtained (see [[#References|[10]]]). The classification of simple singularities and singularities of small modality is related to Lie groups, the Coxeter and Weyl series $ A $, |
| + | $ D $, | ||
| + | $ E $, | ||
| + | the theory of Artin braids, the classification of regular polyhedra in $ 3 $- | ||
| + | dimensional space, the Kodaira classification of degenerate elliptic curves, and the classification of triangles in the Lobachevskii plane (see [[#References|[10]]], ). | ||
===Boundary singularities.=== | ===Boundary singularities.=== | ||
A series of geometric problems requires the study of critical points of functions on a manifold with boundary. | A series of geometric problems requires the study of critical points of functions on a manifold with boundary. | ||
| − | In the complex case this situation corresponds to the study of the germ of a function defined in the space | + | In the complex case this situation corresponds to the study of the germ of a function defined in the space $ \mathbf C ^ {n} $ |
| + | with a distinguished subspace $ \mathbf C ^ {n-} 1 $. | ||
| + | These germs are studied up to changes of variables in $ \mathbf C ^ {n} $ | ||
| + | which transfer $ \mathbf C ^ {n-} 1 $ | ||
| + | onto itself. In this situation, a classification has also been obtained of all simple germs, and of germs of modalities 1 and 2. The classification of simple boundary singularities proves to be related to the simple Lie algebras $ B $, | ||
| + | $ C $ | ||
| + | and $ F _ {4} $. | ||
==Topological characteristics of the germ of a holomorphic function.== | ==Topological characteristics of the germ of a holomorphic function.== | ||
| − | Let | + | Let $ f: ( \mathbf C ^ {n} , 0) \rightarrow ( \mathbf C , 0) $ |
| + | be a holomorphic function in a neighbourhood of zero, with a critical point of multiplicity $ \mu $ | ||
| + | at zero. Let $ \eta , \epsilon $ | ||
| + | be positive numbers, let $ B \subset \mathbf C ^ {n} $ | ||
| + | be the ball $ | x _ {1} | ^ {2} + \dots + | x _ {n} | ^ {2} \leq \epsilon ^ {2} $, | ||
| + | let $ S $ | ||
| + | be its boundary, let $ T \subset \mathbf C $ | ||
| + | be the disc $ | t | < \eta $, | ||
| + | and let $ T ^ \prime $ | ||
| + | be the punctured disc $ T \setminus 0 $. | ||
| + | Let $ X( t) = f ^ { - 1 } ( t) \cap B $ | ||
| + | and $ X = f ^ { - 1 } ( T ^ \prime ) \cap B $. | ||
| + | For appropriate $ \epsilon $ | ||
| + | and $ \eta $( | ||
| + | $ \epsilon $ | ||
| + | is sufficiently small and $ \eta $ | ||
| + | is sufficiently small in relation to $ \epsilon $), | ||
| + | the mapping $ f: X \rightarrow T ^ \prime $ | ||
| + | is a smooth locally trivial fibration. The fibre $ X( t) $ | ||
| + | of this fibration is a $ ( 2n- 2) $- | ||
| + | dimensional manifold with a boundary that is homotopically equivalent to a bouquet of $ \mu $ | ||
| + | $ ( n- 1) $- | ||
| + | dimensional spheres. The boundary of $ X( t) $ | ||
| + | is a $ ( 2n- 3) $- | ||
| + | dimensional manifold which is diffeomorphic to $ f ^ { - 1 } ( 0) \cap S $. | ||
| + | Even for relatively simple $ f $, | ||
| + | this manifold can be non-trivial. For example, the 28 manifolds | ||
| − | + | $$ | |
| + | x _ {1} ^ {6k-} 1 + x _ {2} ^ {3} + x _ {3} ^ {2} + x _ {4} ^ {2} + x _ {5} ^ {2} = 0,\ \ | ||
| + | | x _ {1} | ^ {2} + \dots + | x _ {5} | ^ {2} = \epsilon ^ {2} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | k = 1 \dots 28, | ||
| + | $$ | ||
| − | are 28 Milnor spheres (which are all homeomorphic to an ordinary | + | are 28 Milnor spheres (which are all homeomorphic to an ordinary $ 7 $- |
| + | dimensional sphere, but are not pairwise diffeomorphic). The reduced homology group $ H _ {n-} 1 ( X( t), \star , \mathbf Z ) $ | ||
| + | is isomorphic to $ \mathbf Z ^ \mu $. | ||
| + | The intersection index defines an integer-valued bilinear form on $ H _ {n-} 1 $. | ||
| + | The transfer of fibres of the fibration $ f: X \rightarrow T ^ \prime $ | ||
| + | along curves in $ T ^ \prime $ | ||
| + | defines the action of the fundamental group $ \pi _ {1} ( T ^ \prime ) $ | ||
| + | in the $ ( n- 1) $- | ||
| + | dimensional homology space of the fibre. The automorphism of the homology group corresponding to the generator of $ \pi _ {1} ( T ^ \prime ) $ | ||
| + | is called the monodromy operator. The monodromy operator retains the intersection form. The eigenvalues of the monodromy operator contain information on the asymptotics of various integrals related to the function $ f $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , '''1–2''' , Birkhäuser (1985–1988) (Translated from Russian) {{MR|}} {{ZBL|0659.58002}} {{ZBL|0554.58001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) {{MR|}} {{ZBL|0692.70003}} {{ZBL|0572.70001}} {{ZBL|0647.70001}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Golubitskii, V. Guillemin, "Stable mappings and their singularities" , Springer (1973) {{MR|0467801}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> P. Bröcker, L. Lander, "Differentiable germs and catastrophes" , Cambridge Univ. Press (1975) {{MR|0494220}} {{ZBL|0302.58006}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> T. Poston, I. Stewart, "Catastrophe theory and its applications" , Pitman (1978) {{MR|0501079}} {{ZBL|0382.58006}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J. Milnor, "Singular points of complex hypersurfaces" , Princeton Univ. Press (1968) {{MR|0239612}} {{ZBL|0184.48405}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> , ''Singularities of differentiable mappings'' , Moscow (1968) (In Russian; translated from English and French) {{MR|}} {{ZBL|0933.57028}} {{ZBL|0921.00024}} {{ZBL|0589.58004}} {{ZBL|0545.58001}} {{ZBL|0513.58001}} {{ZBL|0462.00012}} {{ZBL|0299.35043}} {{ZBL|0288.35020}} {{ZBL|0216.45803}} {{ZBL|0216.20105}} {{ZBL|0178.26903}} {{ZBL|0178.26902}} {{ZBL|0061.37005}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> C.G. Gibson, K. Wirthmüller, A.A. du Plessis, E.J.N. Looijenga, "Topological stability of smooth mappings" , ''Lect. notes in math.'' , '''552''' , Springer (1976) {{MR|0436203}} {{ZBL|0377.58006}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> R. Thom, "Structural stability and morphogenesis" , Benjamin (1966) (Translated from French) {{MR|1042988}} {{MR|0488156}} {{ZBL|0698.92001}} {{ZBL|0392.92001}} {{ZBL|0303.92002}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.I. Arnol'd, "Normal forms for functions near degenerate critical points, the Weyl groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620329.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620330.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620331.png" /> and Lagrangian singularities" ''Funct. Anal. Appl.'' , '''6''' : 4 (1972) pp. 254–272 ''Funkts. Anal. i Prilozhen.'' , '''6''' : 4 (1972) pp. 3–25</TD></TR><TR><TD valign="top">[11a]</TD> <TD valign="top"> V.I. Arnol'd, "Lectures on bifurcation in versal families" ''Russian Math. Surveys'' , '''27''' : 5 (1972) pp. 54–123 ''Uspekhi Mat. Nauk'' , '''27''' : 5 (1972) pp. 119–184</TD></TR><TR><TD valign="top">[11b]</TD> <TD valign="top"> V.I. Arnol'd, "Remarks on the stationary phase method and Coxeter numbers" ''Russian Math. Surveys'' , '''28''' : 5 (1973) pp. 19–48 ''Uspekhi Mat. Nauk'' , '''28''' : 5 (1973) pp. 17–44 {{MR|}} {{ZBL|0291.40005}} </TD></TR><TR><TD valign="top">[11c]</TD> <TD valign="top"> V.I. Arnol'd, "Normal forms of functions in a neighbourhood of a degenerate critical point" ''Russian Math. Surveys'' , '''29''' : 2 (1974) pp. 1–5 ''Uspekhi Mat. Nauk'' , '''29''' : 2 (1974) pp. 11–49</TD></TR><TR><TD valign="top">[11d]</TD> <TD valign="top"> V.I. Arnol'd, "Critical points of smooth functions and their normal forms" ''Russian Math. Surveys'' , '''30''' : 5 (1975) pp. 1–75 ''Uspekhi Mat. Nauk'' , '''30''' : 5 (1975) pp. 3–65 {{MR|}} {{ZBL|0343.58001}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> R. Thom, "The bifurcation subspace of a set of maps" N.H. Kuiper (ed.) , ''Manifolds (Amsterdam, 1970)'' , ''Lect. notes in math.'' , '''197''' , Springer (1971) pp. 202–208</TD></TR><TR><TD valign="top">[13a]</TD> <TD valign="top"> A.N. Varchenko, "Local topological properties of differentiable mappings" ''Math. USSR Izv.'' , '''8''' : 5 (1974) pp. 1033–1082 ''Izv. Akad. Nauk SSSR'' , '''38''' : 5 (1974) pp. 1037–1090 {{MR|}} {{ZBL|0313.58009}} </TD></TR><TR><TD valign="top">[13b]</TD> <TD valign="top"> A.N. Varchenko, "A theorem on topological versal deformations" ''Math. USSR Izv.'' , '''9''' : 2 (1975) pp. 277–296 ''Izv. Akad. Nauk SSSR'' , '''39''' : 2 (1975) pp. 294–314 {{MR|}} {{ZBL|0333.32005}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> J. Mather, "Stability of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620332.png" />-mappings III" ''Publ. Math. IHES'' , '''35''' (1969) pp. 127–156; 279–308</TD></TR><TR><TD valign="top">[15a]</TD> <TD valign="top"> J. Mather, "Stability of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620333.png" />-mappings IV" ''Publ. Math. IHES'' , '''37''' (1970) pp. 223–248</TD></TR><TR><TD valign="top">[15b]</TD> <TD valign="top"> J. Mather, "Stability of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620334.png" />-mappings V" ''Adv. Math.'' , '''4''' (1970) pp. 301–335 {{MR|275461}} {{ZBL|}} </TD></TR><TR><TD valign="top">[15c]</TD> <TD valign="top"> J. Mather, "Stability of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620335.png" />-mappings VI" C.T.C. Wall (ed.) , ''Proc. Liverpool Singularities Symposium I'' , ''Lect. notes in math.'' , '''192''' , Springer (1971) pp. 207–253 {{MR|293670}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , '''1–2''' , Birkhäuser (1985–1988) (Translated from Russian) {{MR|}} {{ZBL|0659.58002}} {{ZBL|0554.58001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) {{MR|}} {{ZBL|0692.70003}} {{ZBL|0572.70001}} {{ZBL|0647.70001}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Golubitskii, V. Guillemin, "Stable mappings and their singularities" , Springer (1973) {{MR|0467801}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> P. Bröcker, L. Lander, "Differentiable germs and catastrophes" , Cambridge Univ. Press (1975) {{MR|0494220}} {{ZBL|0302.58006}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> T. Poston, I. Stewart, "Catastrophe theory and its applications" , Pitman (1978) {{MR|0501079}} {{ZBL|0382.58006}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J. Milnor, "Singular points of complex hypersurfaces" , Princeton Univ. Press (1968) {{MR|0239612}} {{ZBL|0184.48405}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> , ''Singularities of differentiable mappings'' , Moscow (1968) (In Russian; translated from English and French) {{MR|}} {{ZBL|0933.57028}} {{ZBL|0921.00024}} {{ZBL|0589.58004}} {{ZBL|0545.58001}} {{ZBL|0513.58001}} {{ZBL|0462.00012}} {{ZBL|0299.35043}} {{ZBL|0288.35020}} {{ZBL|0216.45803}} {{ZBL|0216.20105}} {{ZBL|0178.26903}} {{ZBL|0178.26902}} {{ZBL|0061.37005}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> C.G. Gibson, K. Wirthmüller, A.A. du Plessis, E.J.N. Looijenga, "Topological stability of smooth mappings" , ''Lect. notes in math.'' , '''552''' , Springer (1976) {{MR|0436203}} {{ZBL|0377.58006}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> R. Thom, "Structural stability and morphogenesis" , Benjamin (1966) (Translated from French) {{MR|1042988}} {{MR|0488156}} {{ZBL|0698.92001}} {{ZBL|0392.92001}} {{ZBL|0303.92002}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.I. Arnol'd, "Normal forms for functions near degenerate critical points, the Weyl groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620329.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620330.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620331.png" /> and Lagrangian singularities" ''Funct. Anal. Appl.'' , '''6''' : 4 (1972) pp. 254–272 ''Funkts. Anal. i Prilozhen.'' , '''6''' : 4 (1972) pp. 3–25</TD></TR><TR><TD valign="top">[11a]</TD> <TD valign="top"> V.I. Arnol'd, "Lectures on bifurcation in versal families" ''Russian Math. Surveys'' , '''27''' : 5 (1972) pp. 54–123 ''Uspekhi Mat. Nauk'' , '''27''' : 5 (1972) pp. 119–184</TD></TR><TR><TD valign="top">[11b]</TD> <TD valign="top"> V.I. Arnol'd, "Remarks on the stationary phase method and Coxeter numbers" ''Russian Math. Surveys'' , '''28''' : 5 (1973) pp. 19–48 ''Uspekhi Mat. Nauk'' , '''28''' : 5 (1973) pp. 17–44 {{MR|}} {{ZBL|0291.40005}} </TD></TR><TR><TD valign="top">[11c]</TD> <TD valign="top"> V.I. Arnol'd, "Normal forms of functions in a neighbourhood of a degenerate critical point" ''Russian Math. Surveys'' , '''29''' : 2 (1974) pp. 1–5 ''Uspekhi Mat. Nauk'' , '''29''' : 2 (1974) pp. 11–49</TD></TR><TR><TD valign="top">[11d]</TD> <TD valign="top"> V.I. Arnol'd, "Critical points of smooth functions and their normal forms" ''Russian Math. Surveys'' , '''30''' : 5 (1975) pp. 1–75 ''Uspekhi Mat. Nauk'' , '''30''' : 5 (1975) pp. 3–65 {{MR|}} {{ZBL|0343.58001}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> R. Thom, "The bifurcation subspace of a set of maps" N.H. Kuiper (ed.) , ''Manifolds (Amsterdam, 1970)'' , ''Lect. notes in math.'' , '''197''' , Springer (1971) pp. 202–208</TD></TR><TR><TD valign="top">[13a]</TD> <TD valign="top"> A.N. Varchenko, "Local topological properties of differentiable mappings" ''Math. USSR Izv.'' , '''8''' : 5 (1974) pp. 1033–1082 ''Izv. Akad. Nauk SSSR'' , '''38''' : 5 (1974) pp. 1037–1090 {{MR|}} {{ZBL|0313.58009}} </TD></TR><TR><TD valign="top">[13b]</TD> <TD valign="top"> A.N. Varchenko, "A theorem on topological versal deformations" ''Math. USSR Izv.'' , '''9''' : 2 (1975) pp. 277–296 ''Izv. Akad. Nauk SSSR'' , '''39''' : 2 (1975) pp. 294–314 {{MR|}} {{ZBL|0333.32005}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> J. Mather, "Stability of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620332.png" />-mappings III" ''Publ. Math. IHES'' , '''35''' (1969) pp. 127–156; 279–308</TD></TR><TR><TD valign="top">[15a]</TD> <TD valign="top"> J. Mather, "Stability of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620333.png" />-mappings IV" ''Publ. Math. IHES'' , '''37''' (1970) pp. 223–248</TD></TR><TR><TD valign="top">[15b]</TD> <TD valign="top"> J. Mather, "Stability of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620334.png" />-mappings V" ''Adv. Math.'' , '''4''' (1970) pp. 301–335 {{MR|275461}} {{ZBL|}} </TD></TR><TR><TD valign="top">[15c]</TD> <TD valign="top"> J. Mather, "Stability of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085620/s085620335.png" />-mappings VI" C.T.C. Wall (ed.) , ''Proc. Liverpool Singularities Symposium I'' , ''Lect. notes in math.'' , '''192''' , Springer (1971) pp. 207–253 {{MR|293670}} {{ZBL|}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.I. Arnol'd, "Singularities of caustics and wave fronts" , Kluwer (1990) {{MR|}} {{ZBL|0734.53001}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.I. Arnol'd, "Singularities of caustics and wave fronts" , Kluwer (1990) {{MR|}} {{ZBL|0734.53001}} </TD></TR></table> | ||
Latest revision as of 08:14, 6 June 2020
A branch of mathematical analysis and differential geometry, in which those properties of mappings are studied which are preserved when the coordinates in the image and pre-image of the mapping are changed (or when changes are made which preserve certain supplementary structures); a general approach is proposed to the solution of various problems on degeneration of mappings, functions, vector fields, etc.; a classification is given of the most commonly encountered degenerations, and their normal forms, as well as algorithms which reduce to the normal forms, are determined.
A point of the domain of definition of a differentiable mapping (i.e. a mapping of class $ C ^ {k} $, see Differentiable manifold) is said to be regular if the Jacobi matrix has maximum rank at this point, and critical in the opposite case.
The classical implicit function theorem describes the structure of a mapping in a neighbourhood of a regular point; in a neighbourhood of this point and in a neighbourhood of its image, there exist coordinates in which the mapping is linear.
In many cases it is not sufficient to confine the area of study simply to regular points; it is therefore natural to consider the following questions:
a) the description of a mapping in a neighbourhood of a critical point;
b) the description of the structure of the set of critical points.
For an arbitrary mapping there are no answers to a) and b), for two reasons: In attempting to deal with all mappings, there is no chance of obtaining explicit results (for example, the set of critical points can locally be an arbitrary closed set), and for practical applications it is sufficient to know the answers for only a large set of mappings.
The questions a) and b) and many others in the theory of singularities are studied along the following lines:
1) a set of "untypical" and "pathological" mappings is excluded from consideration;
2) a criterion of "typicality" of a mapping is determined;
3) it is ascertained that every mapping can be approximated by "typical" mappings;
4) the "typical" mappings are studied.
The choice of the set of typical mappings depends on the problem to be solved and is not unique: the fewer the mappings that are typical, the easier they are to study, although 2) and 3) require that the set of typical mappings is sufficiently broad and sufficiently constructively defined.
This scheme is illustrated by the Whitney theorem: Every differentiable mapping $ \mathbf R ^ {2} \rightarrow \mathbf R ^ {2} $ can be approximated by a mapping $ f $ such that for any point $ a \in \mathbf R ^ {2} $ in neighbourhoods of $ a $ and $ f( a) $ coordinates can be chosen at which the mapping $ f $ has one of the three normal forms:
$$ \left \{ \begin{array}{l} y _ {1} = x _ {1} , \\ y _ {2} = x _ {2} ; \end{array} \right . \ \ \left \{ \begin{array}{l} y _ {1} = x _ {1} , \\ y _ {2} = x _ {2} ^ {2} ; \end{array} \right . \ \ \left \{ \begin{array}{l} y _ {1} = x _ {1} , \\ y _ {2} = x _ {2} ^ {3} + x _ {1} x _ {2} \end{array} \right . $$
(for the typicality criterion, see [3], [4]). The work of H. Whitney (1955), in which this theorem was proved, is considered to be the beginning of the theory of singularities of differentiable mappings, although a number of individual results appeared far earlier (Morse theory of critical points of functions, Whitney's theorem on singularities of imbeddings, the work of L.S. Pontryagin on the connection between singularities and characteristic classes).
Basic concepts in the theory of singularities of differentiable mappings.
Germs of differentiable mappings.
Let $ X $ and $ Y $ be smooth manifolds, $ p \in X $, $ q \in Y $. (Hereafter, the term "smooth" will be used as a synonym for infinitely differentiable.) An equivalence class of mappings $ X \rightarrow Y $ which coincide in a certain neighbourhood of the point $ p $ is called a germ at the point $ p $; the set of germs of mappings which transfer $ p $ to $ q $ is denoted by $ C ^ \infty ( X, Y) _ {p,q} $. The group of germs of smooth changes of variables in $ X $ which preserve the point $ p $ is denoted by $ \mathop{\rm Diff} ^ \infty ( X) _ {p} $.
An important local problem in the theory of singularities of differentiable mappings is the study of the natural action of the group
$$ \mathop{\rm Diff} ^ \infty ( X) _ {p} \times \mathop{\rm Diff} ^ \infty ( Y) _ {q} \ \ \mathop{\rm on} C ^ \infty ( X, Y) _ {p,q} . $$
The solution of this and many similar problems is usually begun by approximating the function spaces and the infinite-dimensional groups acting on them by finite-dimensional manifolds and the actions on them by Lie groups. The results obtained are then transferred to the initial infinite-dimensional situation.
Jet bundles.
Let $ f, g: X \rightarrow Y $ be smooth mappings, and let $ f( p) = g( p) = q $; the mappings $ f $ and $ g $ have, by definition, contact of order $ k $ at the point $ p $ if their Taylor series at this point coincide up to the order $ k $. An equivalence class of mappings which have contact of order $ k $ at the point $ p $ is called a $ k $- jet. The set of all $ k $- jets of mappings which transfer $ p $ to $ q $ has the natural structure of a smooth manifold and is denoted by $ J ^ {k} ( X, Y) _ {p,q} $. There is a well-defined natural projection
$$ C ^ \infty ( X, Y) _ {p,q} \rightarrow J ^ {k} ( X, Y) _ {p,q} . $$
The equivalence class of smooth changes of variables in $ X $ which preserve the point $ p $ and have contact of order $ k $ at this point is called an invertible $ k $- jet at $ p $. The invertible $ k $- jets form a Lie group $ L ^ {k} ( X) _ {p} $. The Lie group $ L ^ {k} ( X) _ {p} \times L ^ {k} ( Y) _ {q} $ acts on $ J ^ {k} ( X, Y) _ {p,q} $ and approximates the action of
$$ \mathop{\rm Diff} ^ \infty ( X) _ {p} \times \mathop{\rm Diff} ^ \infty ( Y) _ {q} \ \ \mathop{\rm on} C ^ \infty ( X, Y) _ {p,q} . $$
Let $ J ^ {k} ( X, Y) = \{ \textrm{ disjoint union of } J ^ {k} ( X, Y) _ {p,q } \textrm{ over { } all } ( p, q) \in X \times Y \} $. The set $ J ^ {k} ( X, Y) $ has the natural structure of a smooth bundle over $ X \times Y $ with fibre
$$ J ^ {k} ( \mathbf R ^ {m} , \mathbf R ^ {n} ) _ {0,0} = J ^ {k} ( m, n) $$
and structure group
$$ L ^ {k} ( \mathbf R ^ {m} ) _ {0} \times L ^ {k} ( \mathbf R ^ {n} ) _ {0} = \ L ^ {k} ( m, n), $$
where $ m = \mathop{\rm dim} X $, $ n = \mathop{\rm dim} Y $.
Singularities and classes of singularities.
An orbit of the action of $ L ^ {k} ( m, n) $ on $ J ^ {k} ( m, n) $ is called a $ k $- singularity; any subset in $ J ^ {k} ( m, n) $ that is invariant under $ L ^ {k} ( m, n) $ is called a class of $ k $- singularities. Let $ S $ be such a class. Because $ J ^ {k} ( m, n) $ can be identified with $ J ^ {k} ( X, Y) _ {p,q} $, the subset $ S( X, Y) _ {p,q} $ is defined in $ J ^ {k} ( X, Y) _ {p,q} $, irrespective of the method of identification. The set $ S( X, Y) = \{ \textrm{ union of } S( X, Y) _ {p,q} \textrm{ over { } all } ( p, q) \in X \times Y \} $ is called a universal class of singularities (or a universal singularity if $ S $ is a singularity). A universal singularity $ S( X, Y) $ is a submanifold in $ J ^ {k} ( X, Y) $ of codimension equal to the codimension of $ S $ in $ J ^ {k} ( m, n) $.
Let $ F: X \rightarrow Y $ be a smooth mapping. The smooth mapping $ j ^ {k} f: X \rightarrow J ^ {k} ( X, Y) $, called the $ k $- jet extension of $ f $, is obtained by assigning to each point $ p \in X $ the $ k $- jet of $ f $ at $ p $. The mapping $ f: X \rightarrow Y $ has, by definition, a singularity of type $ S $ at the point $ p $ if $ j ^ {k} f( p) \in S( X, Y) $. The set $ S( f ) $ of all points at which $ f $ has a singularity of type $ S $ is none other than $ ( j ^ {k} f ) ^ {-} 1 S( X, Y) $. The study of the set $ S( f ) $ thus divides into two stages: the study of the universal set $ S( X, Y) $ in $ J ^ {k} ( X, Y) $, which reduces to the study of $ S $ in $ J ^ {k} ( m, n) $, and the study of the mutual positions of $ S( X, Y) $ and $ j ^ {k} f( X) $. In the second stage one usually employs Thom's transversality theorem.
Transversality.
A smooth mapping $ f: A\rightarrow B $ of smooth manifolds is transversal to a submanifold $ C \subset B $( denoted $ f \perp C $) if for any point $ a \in A $ either $ f( a) \notin C $ or $ ( df ) _ {a} ( T _ {a} A) \oplus T _ {f(} a) C = T _ {f(} a) B $. If $ f \perp C $, then the set $ f ^ { - 1 } ( C) $ is either empty or is a submanifold in $ A $ of codimension equal to the codimension of $ C $ in $ B $.
Thom's transversality theorem: Let $ X, Y $ be smooth manifolds and let $ C $ be a submanifold in $ J ^ {k} ( X, Y) $; then the set of those $ f $ for which $ j ^ {k} f \perp C $ is a massive subset in $ C ^ \infty ( X, Y) $ in the Whitney $ C ^ \infty $- topology. (A set is said to be massive (generic) if it is the intersection of a countable number of open dense subsets. A property is called generic if it holds for all $ f $ in a generic subset.)
The Whitney topology. Let $ k \geq 0 $ and let $ U $ be an open set in $ J ^ {k} ( X, Y) $. Let
$$ M( U) = \{ {f \in C ^ \infty ( X, Y) } : {j ^ {k} f( X) \subset U } \} . $$
The sets $ M( U) $ form the basis of some topology, called the Whitney $ C ^ \infty $- topology, on $ C ^ \infty ( X, Y) $. In this topology, $ C ^ \infty ( X, Y) $ is a Baire space, i.e. every massive subset is dense.
Multi-jets.
In the study of the self-intersection of the image of a smooth mapping, the concept of a multi-jet is used. Let $ \alpha : J ^ {k} ( X, Y) \rightarrow X $ be the natural projection. Let
$$ X ^ {(} s) = \{ {( x _ {1} \dots x _ {s} ) \in X \times \dots \times X } : { x _ {j} \neq x _ {i} , i \neq j } \} $$
and let $ \alpha ^ {s} = \alpha \times \dots \times \alpha $( $ s $ times). The set $ J _ {s} ^ {k} ( X, Y) = ( \alpha ^ {s} ) ^ {-} 1 ( X ^ {(} s) ) $ may be given the natural structure of a smooth manifold and is called an $ s $- fold bundle of $ k $- jets. For $ s $- fold jets, the $ k $- jet extension of a mapping $ f $, $ k $- singularities, universal singularities, etc., are defined, and the analogue of Thom's transversality theorem has been proved.
Stable differentiable mappings.
A central problem in the early days of the theory of singularities of differentiable mappings was the study of stable differentiable mappings.
A smooth mapping $ f: X ^ {m} \rightarrow Y ^ {n} $ of smooth manifolds is said to be stable if for any mapping $ \widetilde{f} $ that is sufficiently close to $ f $ there exists diffeomorphisms $ h: X ^ {m} \rightarrow X ^ {m} $ and $ k: Y ^ {n} \rightarrow Y ^ {n} $ such that $ \widetilde{f} = h \circ f \circ k $.
For small $ m, n $( $ m, n \leq 4 $), as well as for $ n= 1 $ and any $ m $, stable differentiable mappings are dense in the space of all proper differentiable mappings [3]. In the space of mappings $ X ^ {9} \rightarrow Y ^ {9} $, stable mappings do not form an everywhere-dense set (see [1]). For certain pairs of manifolds (for example, for $ X = \mathbf R P ^ {19} $, $ Y = \mathbf R ^ {19} $) there is no stable mapping from $ X $ into $ Y $. All "stable dimensions" $ ( m, n) $ have been found in [14], : For any smooth manifolds $ X ^ {m} $ and $ Y ^ {n} $, the stable mappings from $ X ^ {m} $ into $ Y ^ {n} $ are dense in the space of proper differentiable mappings $ X ^ {m} \rightarrow Y ^ {n} $, equipped with the Whitney $ C ^ \infty $- topology, if and only if the pair $ ( m, n) $ satisfies at least one of the following conditions $ ( q = n- m) $: a) $ n < 7q + 8 $ and $ q \geq 4 $; b) $ n < 7q + 9 $ and $ 3 \geq q \geq 0 $; c) $ n < 8 $ and $ q = - 1 $; d) $ n < 6 $ and $ q = - 2 $; e) $ n < 7 $ and $ q \leq 3 $.
In proving this theorem, as well as in many other questions, the following two concepts prove to be useful: A mapping $ f _ {0} : X ^ {m} \rightarrow Y ^ {n} $ is called homotopy stable if for any smooth homotopy $ f _ {t} $ of the mapping $ f _ {0} $ there are smooth homotopies $ h _ {t} $ and $ k _ {t} $ of the identity diffeomorphisms of $ X ^ {m} $ and $ Y ^ {n} $ such that $ f _ {t} = h _ {t} \circ f _ {0} \circ k _ {t} $ for sufficiently small $ t $. A mapping $ f: X ^ {m} \rightarrow Y ^ {n} $ is called infinitesimal stable if every mapping $ \widetilde{f} $ that is infinitely close to $ f _ {0} $ can be obtained from $ f _ {0} $ by diffeomorphisms of $ X ^ {m} $ and $ Y ^ {n} $ which are "infinitely close to the identity" . For a proper mapping, the concepts of stability, homotopy stability and infinitesimal stability coincide [3]. The problem of finding local normal forms of stable mappings reduces to the problem of classifying certain finite-dimensional local algebras [14], . For fixed $ m, n $, the number of such normal forms is finite.
If in the definition of a stable mapping, homeomorphisms $ h $ and $ k $ are taken instead of diffeomorphisms, then the definition of a topologically stable mapping is obtained. The theorem on the density of the set of topological stable mappings in the set of all mappings of any compact manifold $ X ^ {m} $ into any manifold $ Y ^ {n} $( for any $ m, n $) has been proved (see [8]).
Finitely defined germs.
Let $ \sim $ be some equivalence relation on the set $ C ^ \infty ( \mathbf R ^ {m} , \mathbf R ^ {n} ) _ {0,0} $ of germs of mappings $ \mathbf R ^ {m} \rightarrow \mathbf R ^ {n} $ which take $ 0 $ to $ 0 $. The $ k $- jet of any such germ is the segment of order $ k $ of its Taylor series. A germ $ f $ is said to be $ k $- defined if any other germ $ g $ with the same $ k $- jet satisfies the relation $ f \sim g $. A germ is finitely defined if it is $ k $- defined for a certain $ k $. A $ k $- jet $ \sigma $ such that any two germs $ f, g $ which have $ \sigma $ as $ k $- jet satisfy the relation $ f \sim g $, is said to be sufficient. The most commonly encountered equivalences have special names:
$ r $- equivalence — belonging to one orbit of the group $ \mathop{\rm Diff} ^ \infty ( \mathbf R ^ {m} ) _ {0} $ of "correct" changes of coordinates.
$ rl $- equivalence — belonging to one orbit of the group $ \mathop{\rm Diff} ^ \infty ( \mathbf R ^ {m} ) _ {0} \times \mathop{\rm Diff} ^ \infty ( \mathbf R ^ {n} ) _ {0} $.
Topological equivalence — belonging to one orbit of the group $ \mathop{\rm Diff} ^ {0} ( \mathbf R ^ {m} ) _ {0} \times \mathop{\rm Diff} ^ {0} ( \mathbf R ^ {n} ) _ {0} $.
The study of $ k $- defined germs reduces to the study of mappings defined by polynomials of degree $ \leq k $.
The question of whether a germ is $ k $- defined with respect to $ rl $- equivalence reduces to the problem of the solvability of an explicit system of finitely many linear equations.
The set of finitely defined germs with respect to $ rl $- equivalence is open in $ C ^ \infty ( \mathbf R ^ {m} , \mathbf R ^ {n} ) _ {0,0} $, but is not dense for any $ m, n $. It is natural to consider the coarser relation of topological equivalence. After rejection of a subset of finite codimension from $ C ^ \infty ( \mathbf R ^ {m} , \mathbf R ^ {n} ) _ {0,0} $, a countable number of topological equivalence classes remains, each of which is a semi-algebraic set. It follows that the mappings with germs that are topologically equivalent to polynomial ones form an open dense set in $ C ^ \infty ( X, Y) $( $ X ^ {m} $ is compact) .
Deformation.
If a mapping depends on parameters, then a family of mappings is said to be defined. If the family of mappings is studied locally, then when the parameters are changed slightly in a neighbourhood of fixed values, one speaks of a deformation of the mapping corresponding to these fixed values of the parameters. In many cases, the study of all possible deformations reduces to the study of a single natural deformation, from which all others are obtained. This deformation, in a sense the largest, contains all essentially different deformations of the given mapping. It is called the versal deformation (see , [12], ).
Critical points of functions.
A critical point of a function is called non-degenerate if the second differential is a non-degenerate quadratic form. A function in general position has only non-degenerate critical points, while in a neighbourhood of each of them it can be reduced to a standard form. Degenerate critical points are studied when these functions depend on parameters, and the greater the number of these parameters, the more complex critical points will be encountered that are non-removable (by a small shift) for certain values of the parameters.
A family of functions depending on any number of parameters can be transformed by a small shift into a family in which, for every value of the parameter in a neighbourhood of any point of the domain of definition, the function is represented by a polynomial in a local system of coordinates. This means that in the local study of functions it is possible to examine only polynomials and to use complex analysis.
Classification.
It is natural to begin by classifying the germs at 0 of holomorphic functions in $ \mathbf C ^ {n} $, taking two germs to be equivalent if one can be transferred into the other by the germ of a holomorphic change of coordinates in $ \mathbf C ^ {n} $ which preserves 0. A jet (Taylor polynomial) of a holomorphic function at 0 is sufficient if it defines the function up to equivalence. A germ whose critical point 0 is isolated always has a sufficient jet and, consequently, is equivalent to a polynomial. The number of non-degenerate critical points into which the critical point 0 splits when the function is shifted slightly is called the multiplicity (or Milnor number) $ \mu $ of the critical point 0. If the multiplicity of a critical point of a function $ f $ is equal to $ \mu $, then the $ ( \mu + 1) $- jet is sufficient. Since the multiplicity $ \mu $ cannot increase under a small change of $ f $, the classification of functions close to a function with an isolated critical point reduces to the study of the action of the Lie group of $ k $- jets of changes of variables on the space of $ k $- jets for a sufficiently large $ k $. In a space of $ k $- jets of functions $ f $ for which $ f( 0) = 0 $, $ df( 0) = 0 $, the codimension of the orbit of $ f $ is equal to $ \mu - 1 $; thus, the critical points of multiplicity $ \mu $ are non-removable in families of functions which depend on $ ( \mu - 1) $ parameters. A classification (see [10]) of all critical points of multiplicity $ \mu \leq 16 $ and an algorithm for reducing any such function to a normal form have been obtained. The complexity of a critical point is defined not only by its multiplicity $ \mu $, but also by its modality $ m $( the number of moduli). A critical point is simple (or $ 0 $- modal) if among the critical points near to it there are at most finitely many pairwise non-equivalent points. Two germs of functions are called stably equivalent if they become equivalent after being added directly to non-degenerate quadratic forms in the appropriate number of variables (for germs of functions in the same number of variables, stable equivalence is the same ordinary equivalence).
Simple germs are exhausted up to stable equivalence by the following list:
$ A _ {k} $: $ f( x) = x ^ {k+} 1 $, $ k \geq 1 $;
$ D _ {k} $: $ f( x, y) = x ^ {2} y + y ^ {k-} 1 $, $ k \geq 4 $;
$ E _ {6} $: $ f( x, y) = x ^ {3} + y ^ {4} $;
$ E _ {7} $: $ f( x, y) = x ^ {3} + xy ^ {3} $;
$ E _ {8} $: $ f( x, y) = x ^ {3} + y ^ {5} $.
The modality of a point $ x \in X $ under the action of a Lie group $ G $ on a manifold $ X $ is the smallest number $ m $ such that a sufficiently small neighbourhood of $ x $ is covered by a finite number of $ m $- parametric families of orbits.
A classification of germs of functions of modality 1 and 2 has also been obtained (see [10]). The classification of simple singularities and singularities of small modality is related to Lie groups, the Coxeter and Weyl series $ A $, $ D $, $ E $, the theory of Artin braids, the classification of regular polyhedra in $ 3 $- dimensional space, the Kodaira classification of degenerate elliptic curves, and the classification of triangles in the Lobachevskii plane (see [10], ).
Boundary singularities.
A series of geometric problems requires the study of critical points of functions on a manifold with boundary.
In the complex case this situation corresponds to the study of the germ of a function defined in the space $ \mathbf C ^ {n} $ with a distinguished subspace $ \mathbf C ^ {n-} 1 $. These germs are studied up to changes of variables in $ \mathbf C ^ {n} $ which transfer $ \mathbf C ^ {n-} 1 $ onto itself. In this situation, a classification has also been obtained of all simple germs, and of germs of modalities 1 and 2. The classification of simple boundary singularities proves to be related to the simple Lie algebras $ B $, $ C $ and $ F _ {4} $.
Topological characteristics of the germ of a holomorphic function.
Let $ f: ( \mathbf C ^ {n} , 0) \rightarrow ( \mathbf C , 0) $ be a holomorphic function in a neighbourhood of zero, with a critical point of multiplicity $ \mu $ at zero. Let $ \eta , \epsilon $ be positive numbers, let $ B \subset \mathbf C ^ {n} $ be the ball $ | x _ {1} | ^ {2} + \dots + | x _ {n} | ^ {2} \leq \epsilon ^ {2} $, let $ S $ be its boundary, let $ T \subset \mathbf C $ be the disc $ | t | < \eta $, and let $ T ^ \prime $ be the punctured disc $ T \setminus 0 $. Let $ X( t) = f ^ { - 1 } ( t) \cap B $ and $ X = f ^ { - 1 } ( T ^ \prime ) \cap B $. For appropriate $ \epsilon $ and $ \eta $( $ \epsilon $ is sufficiently small and $ \eta $ is sufficiently small in relation to $ \epsilon $), the mapping $ f: X \rightarrow T ^ \prime $ is a smooth locally trivial fibration. The fibre $ X( t) $ of this fibration is a $ ( 2n- 2) $- dimensional manifold with a boundary that is homotopically equivalent to a bouquet of $ \mu $ $ ( n- 1) $- dimensional spheres. The boundary of $ X( t) $ is a $ ( 2n- 3) $- dimensional manifold which is diffeomorphic to $ f ^ { - 1 } ( 0) \cap S $. Even for relatively simple $ f $, this manifold can be non-trivial. For example, the 28 manifolds
$$ x _ {1} ^ {6k-} 1 + x _ {2} ^ {3} + x _ {3} ^ {2} + x _ {4} ^ {2} + x _ {5} ^ {2} = 0,\ \ | x _ {1} | ^ {2} + \dots + | x _ {5} | ^ {2} = \epsilon ^ {2} , $$
$$ k = 1 \dots 28, $$
are 28 Milnor spheres (which are all homeomorphic to an ordinary $ 7 $- dimensional sphere, but are not pairwise diffeomorphic). The reduced homology group $ H _ {n-} 1 ( X( t), \star , \mathbf Z ) $ is isomorphic to $ \mathbf Z ^ \mu $. The intersection index defines an integer-valued bilinear form on $ H _ {n-} 1 $. The transfer of fibres of the fibration $ f: X \rightarrow T ^ \prime $ along curves in $ T ^ \prime $ defines the action of the fundamental group $ \pi _ {1} ( T ^ \prime ) $ in the $ ( n- 1) $- dimensional homology space of the fibre. The automorphism of the homology group corresponding to the generator of $ \pi _ {1} ( T ^ \prime ) $ is called the monodromy operator. The monodromy operator retains the intersection form. The eigenvalues of the monodromy operator contain information on the asymptotics of various integrals related to the function $ f $.
References
| [1] | V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 1–2 , Birkhäuser (1985–1988) (Translated from Russian) Zbl 0659.58002 Zbl 0554.58001 |
| [2] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) Zbl 0692.70003 Zbl 0572.70001 Zbl 0647.70001 |
| [3] | M. Golubitskii, V. Guillemin, "Stable mappings and their singularities" , Springer (1973) MR0467801 |
| [4] | P. Bröcker, L. Lander, "Differentiable germs and catastrophes" , Cambridge Univ. Press (1975) MR0494220 Zbl 0302.58006 |
| [5] | T. Poston, I. Stewart, "Catastrophe theory and its applications" , Pitman (1978) MR0501079 Zbl 0382.58006 |
| [6] | J. Milnor, "Singular points of complex hypersurfaces" , Princeton Univ. Press (1968) MR0239612 Zbl 0184.48405 |
| [7] | , Singularities of differentiable mappings , Moscow (1968) (In Russian; translated from English and French) Zbl 0933.57028 Zbl 0921.00024 Zbl 0589.58004 Zbl 0545.58001 Zbl 0513.58001 Zbl 0462.00012 Zbl 0299.35043 Zbl 0288.35020 Zbl 0216.45803 Zbl 0216.20105 Zbl 0178.26903 Zbl 0178.26902 Zbl 0061.37005 |
| [8] | C.G. Gibson, K. Wirthmüller, A.A. du Plessis, E.J.N. Looijenga, "Topological stability of smooth mappings" , Lect. notes in math. , 552 , Springer (1976) MR0436203 Zbl 0377.58006 |
| [9] | R. Thom, "Structural stability and morphogenesis" , Benjamin (1966) (Translated from French) MR1042988 MR0488156 Zbl 0698.92001 Zbl 0392.92001 Zbl 0303.92002 |
| [10] | V.I. Arnol'd, "Normal forms for functions near degenerate critical points, the Weyl groups 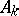 , , 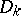 , , 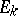 and Lagrangian singularities" Funct. Anal. Appl. , 6 : 4 (1972) pp. 254–272 Funkts. Anal. i Prilozhen. , 6 : 4 (1972) pp. 3–25 and Lagrangian singularities" Funct. Anal. Appl. , 6 : 4 (1972) pp. 254–272 Funkts. Anal. i Prilozhen. , 6 : 4 (1972) pp. 3–25 |
| [11a] | V.I. Arnol'd, "Lectures on bifurcation in versal families" Russian Math. Surveys , 27 : 5 (1972) pp. 54–123 Uspekhi Mat. Nauk , 27 : 5 (1972) pp. 119–184 |
| [11b] | V.I. Arnol'd, "Remarks on the stationary phase method and Coxeter numbers" Russian Math. Surveys , 28 : 5 (1973) pp. 19–48 Uspekhi Mat. Nauk , 28 : 5 (1973) pp. 17–44 Zbl 0291.40005 |
| [11c] | V.I. Arnol'd, "Normal forms of functions in a neighbourhood of a degenerate critical point" Russian Math. Surveys , 29 : 2 (1974) pp. 1–5 Uspekhi Mat. Nauk , 29 : 2 (1974) pp. 11–49 |
| [11d] | V.I. Arnol'd, "Critical points of smooth functions and their normal forms" Russian Math. Surveys , 30 : 5 (1975) pp. 1–75 Uspekhi Mat. Nauk , 30 : 5 (1975) pp. 3–65 Zbl 0343.58001 |
| [12] | R. Thom, "The bifurcation subspace of a set of maps" N.H. Kuiper (ed.) , Manifolds (Amsterdam, 1970) , Lect. notes in math. , 197 , Springer (1971) pp. 202–208 |
| [13a] | A.N. Varchenko, "Local topological properties of differentiable mappings" Math. USSR Izv. , 8 : 5 (1974) pp. 1033–1082 Izv. Akad. Nauk SSSR , 38 : 5 (1974) pp. 1037–1090 Zbl 0313.58009 |
| [13b] | A.N. Varchenko, "A theorem on topological versal deformations" Math. USSR Izv. , 9 : 2 (1975) pp. 277–296 Izv. Akad. Nauk SSSR , 39 : 2 (1975) pp. 294–314 Zbl 0333.32005 |
| [14] | J. Mather, "Stability of 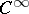 -mappings III" Publ. Math. IHES , 35 (1969) pp. 127–156; 279–308 -mappings III" Publ. Math. IHES , 35 (1969) pp. 127–156; 279–308 |
| [15a] | J. Mather, "Stability of 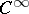 -mappings IV" Publ. Math. IHES , 37 (1970) pp. 223–248 -mappings IV" Publ. Math. IHES , 37 (1970) pp. 223–248 |
| [15b] | J. Mather, "Stability of 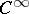 -mappings V" Adv. Math. , 4 (1970) pp. 301–335 MR275461 -mappings V" Adv. Math. , 4 (1970) pp. 301–335 MR275461 |
| [15c] | J. Mather, "Stability of 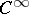 -mappings VI" C.T.C. Wall (ed.) , Proc. Liverpool Singularities Symposium I , Lect. notes in math. , 192 , Springer (1971) pp. 207–253 MR293670 -mappings VI" C.T.C. Wall (ed.) , Proc. Liverpool Singularities Symposium I , Lect. notes in math. , 192 , Springer (1971) pp. 207–253 MR293670 |
Comments
References
| [a1] | V.I. Arnol'd, "Singularities of caustics and wave fronts" , Kluwer (1990) Zbl 0734.53001 |
Singularities of differentiable mappings. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Singularities_of_differentiable_mappings&oldid=24128