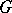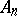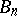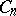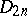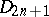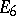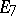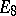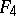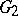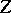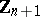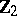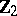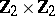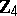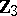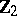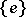Difference between revisions of "Simply-connected group"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(Tex partly done) |
||
| Line 1: | Line 1: | ||
A [[Topological group|topological group]] (in particular, a [[Lie group|Lie group]]) for which the underlying topological space is simply-connected. The significance of simply-connected groups in the theory of Lie groups is explained by the following theorems. | A [[Topological group|topological group]] (in particular, a [[Lie group|Lie group]]) for which the underlying topological space is simply-connected. The significance of simply-connected groups in the theory of Lie groups is explained by the following theorems. | ||
| − | 1) Every connected Lie group | + | 1) Every connected Lie group $G$ is isomorphic to the quotient group of a certain simply-connected group (called the universal covering of $G$) by a discrete central subgroup isomorphic to $\pi_1(G)$. |
| − | 2) Two simply-connected Lie groups are isomorphic if and only if their Lie algebras are isomorphic; furthermore, every homomorphism of the Lie algebra of a simply-connected group | + | 2) Two simply-connected Lie groups are isomorphic if and only if their Lie algebras are isomorphic; furthermore, every homomorphism of the Lie algebra of a simply-connected group $G_1$ into the Lie algebra of an arbitrary Lie group $G_2$ is the derivation of a (uniquely defined) homomorphism of $G_1$ into $G_2$. |
| − | The centre | + | The centre $Z$ of a simply-connected semi-simple compact or complex Lie group $G$ is finite. It is given in the following table for the various kinds of simple Lie groups. |
| + | |||
| + | <table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543010.png" /></td> <td colname="2" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543011.png" /></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543012.png" /></td> <td colname="4" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543013.png" /></td> <td colname="5" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543014.png" /></td> <td colname="6" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543015.png" /></td> <td colname="7" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543016.png" /></td> <td colname="8" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543017.png" /></td> <td colname="9" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543018.png" /></td> <td colname="10" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543019.png" /></td> <td colname="11" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543020.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543021.png" /></td> <td colname="2" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543022.png" /></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543023.png" /></td> <td colname="4" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543024.png" /></td> <td colname="5" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543025.png" /></td> <td colname="6" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543026.png" /></td> <td colname="7" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543027.png" /></td> <td colname="8" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543028.png" /></td> <td colname="9" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543029.png" /></td> <td colname="10" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543030.png" /></td> <td colname="11" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085430/s08543031.png" /></td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
| − | In the theory of | + | In the theory of [[algebraic group]]s, a simply-connected group is a connected algebraic group $G$ not admitting any non-trivial [[isogeny]] $\phi : \tilde G \rightarrow G$, where $\tilde G$ is also a connected algebraic group. For semi-simple algebraic groups over the field of complex numbers this definition is equivalent to that given above. |
| Line 17: | Line 19: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Hochschild, "The structure of Lie groups" , Holden-Day (1965) {{MR|0207883}} {{ZBL|0131.02702}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Hermann, "Lie groups for physicists" , Benjamin (1966) {{MR|0213463}} {{ZBL|0135.06901}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.E. Humphreys, "Linear algebraic groups" , Springer (1975) pp. Sect. 35.1 {{MR|0396773}} {{ZBL|0325.20039}} </TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Hochschild, "The structure of Lie groups" , Holden-Day (1965) {{MR|0207883}} {{ZBL|0131.02702}} </TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Hermann, "Lie groups for physicists" , Benjamin (1966) {{MR|0213463}} {{ZBL|0135.06901}} </TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> J.E. Humphreys, "Linear algebraic groups" , Springer (1975) pp. Sect. 35.1 {{MR|0396773}} {{ZBL|0325.20039}} </TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 18:48, 19 November 2016
A topological group (in particular, a Lie group) for which the underlying topological space is simply-connected. The significance of simply-connected groups in the theory of Lie groups is explained by the following theorems.
1) Every connected Lie group $G$ is isomorphic to the quotient group of a certain simply-connected group (called the universal covering of $G$) by a discrete central subgroup isomorphic to $\pi_1(G)$.
2) Two simply-connected Lie groups are isomorphic if and only if their Lie algebras are isomorphic; furthermore, every homomorphism of the Lie algebra of a simply-connected group $G_1$ into the Lie algebra of an arbitrary Lie group $G_2$ is the derivation of a (uniquely defined) homomorphism of $G_1$ into $G_2$.
The centre $Z$ of a simply-connected semi-simple compact or complex Lie group $G$ is finite. It is given in the following table for the various kinds of simple Lie groups.
<tbody> </tbody>
|
In the theory of algebraic groups, a simply-connected group is a connected algebraic group $G$ not admitting any non-trivial isogeny $\phi : \tilde G \rightarrow G$, where $\tilde G$ is also a connected algebraic group. For semi-simple algebraic groups over the field of complex numbers this definition is equivalent to that given above.
Comments
References
| [a1] | G. Hochschild, "The structure of Lie groups" , Holden-Day (1965) MR0207883 Zbl 0131.02702 |
| [a2] | R. Hermann, "Lie groups for physicists" , Benjamin (1966) MR0213463 Zbl 0135.06901 |
| [a3] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) pp. Sect. 35.1 MR0396773 Zbl 0325.20039 |
Simply-connected group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simply-connected_group&oldid=21937