Shock waves, mathematical theory of
A mathematical description of properties, motions and interactions with the surrounding medium of a surface of discontinuity of the parameters of a medium (a so-called shock wave). In a wider and more abstract sense the mathematical theory of shock waves describes the properties of a surface of discontinuity of a solution of a first-order quasi-linear hyperbolic system of partial differential equations (cf. Quasi-linear hyperbolic equations and systems). The mathematical theory of shock waves arose in connection with problems of the motion of gases and compressible fluids in the second half of the 19th century. Its foundations were established in the works of S. Earnshaw, B. Riemann, W. Rankine, H. Hugoniot (cf., for example, [1]–[4]).
As an idealization of real gases and fluids one considers a medium without dissipation, lacking viscosity and thermal conductivity. In the process of motion in such idealized media there may arise discontinuities in the distribution of all parameters of the flow (the density, the pressure, the temperature, the velocity, etc.). The set of discontinuity points of the parameters of the flow may be very complicated. Only the simplest basic cases have been systematically considered, when this set has piecewise-smooth surfaces of discontinuity consisting of discontinuity points of the parameter of the first kind. In the general case two-dimensional surfaces of discontinuity move in the three-dimensional space 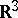 with the flow of time. Shock waves are one of the possible types of surfaces of discontinuity.
with the flow of time. Shock waves are one of the possible types of surfaces of discontinuity.
The appearance of discontinuities very much complicates the mathematical formulation of the problem of the flow of ideal gases and fluids, because discontinuous functions cannot be solutions of the differential equations of gas dynamics (hydrodynamics). Therefore the flows with surfaces of discontinuity are described by generalized solutions of systems of quasi-linear equations of gas dynamics (cf. Gas dynamics, equations of) and the mathematical theory of shock waves forms part of the theory of generalized solutions of the systems of integral conservation laws of gas dynamics.
Surfaces of discontinuity.
On the surfaces of discontinuity the conditions that follow from the integral conservation laws of mass, momentum and energy have to be satisfied. The only exception are the discontinuities at the moment of starting the motion (the so-called initial discontinuities), which may be arbitrary. Let 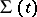 be a smooth surface of discontinuity of the parameters of a flow of a gas (fluid), and let
be a smooth surface of discontinuity of the parameters of a flow of a gas (fluid), and let 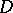 be the normal velocity of the motion of the surface of discontinuity. Only homogeneous media which are characterized by a density
be the normal velocity of the motion of the surface of discontinuity. Only homogeneous media which are characterized by a density 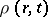 , a pressure
, a pressure 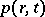 , an internal energy of a unit mass of gas
, an internal energy of a unit mass of gas 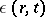 , and a velocity vector of the motion of the medium
, and a velocity vector of the motion of the medium 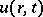 will be considered here.
will be considered here.
In a point of the surface  , let
, let 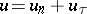 , where
, where 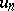 is the normal and
is the normal and 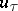 the tangential velocity component (relative to
the tangential velocity component (relative to 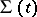 ) of the velocity vector
) of the velocity vector  . The continuity conditions for the flow of mass, momentum and energy on the surface
. The continuity conditions for the flow of mass, momentum and energy on the surface 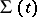 are expressed in the form of equations:
are expressed in the form of equations:
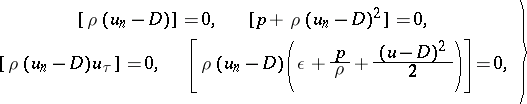 | (1) |
where the square brackets denote the jump in the value of the quantity enclosed in passing from one side of the surface to the other, i.e. 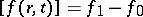 , where
, where 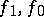 are the limit values of the quantity
are the limit values of the quantity 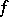 at the point
at the point  when approaching from the two sides. Conditions (1) are intrinsic boundary conditions which are added to the equations of gas dynamics on surfaces of discontinuity of the parameters of the medium.
when approaching from the two sides. Conditions (1) are intrinsic boundary conditions which are added to the equations of gas dynamics on surfaces of discontinuity of the parameters of the medium.
There are two types of discontinuity: a tangential discontinuity for 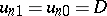 ;
; 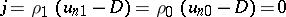 , and shock waves for
, and shock waves for 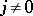 . The vector
. The vector  is called the mass flow across unit area of the moving surface of discontinuity (shock wave)
is called the mass flow across unit area of the moving surface of discontinuity (shock wave) 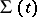 .
.
Tangential and contact discontinuities.
For a tangential discontinuity  the pressure is continuous,
the pressure is continuous, 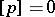 on
on  , while the quantities
, while the quantities 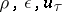 may have arbitrary jumps on
may have arbitrary jumps on 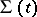 . If at least one of the quantities
. If at least one of the quantities 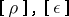 is different from zero, the discontinuity is also called a contact discontinuity. In the case of a contact discontinuity the surface
is different from zero, the discontinuity is also called a contact discontinuity. In the case of a contact discontinuity the surface 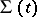 is the dividing boundary of the media with different properties, in particular with different equations of state; it is formed by the lines of flow emitted from the surface of the initial contact discontinuity.
is the dividing boundary of the media with different properties, in particular with different equations of state; it is formed by the lines of flow emitted from the surface of the initial contact discontinuity.
A tangential discontinuity (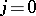 ,
, 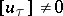 ) is unstable, because under the action of even a small viscosity intrinsic to the gases and fluids, the initial tangential discontinuity represented by the component
) is unstable, because under the action of even a small viscosity intrinsic to the gases and fluids, the initial tangential discontinuity represented by the component 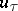 of the velocity vector diffuses into a much wider zone of continuous transition. With the exception of singular cases, when this discontinuity is realized in a short interval of time (tangential discontinuity in a nozzle, initial regions of a zone of mixing of different flows, etc.), one does not consider it as an admissible discontinuity. This is a manifestation of the limitations imposed by considering "ideal" media or media with a small viscosity, since in an ideal medium the tangential discontinuity is preserved. Therefore the question of the admissibility or non-admissibility of the tangential discontinuity of the flow of an ideal medium has to be analyzed for each separate concrete problem.
of the velocity vector diffuses into a much wider zone of continuous transition. With the exception of singular cases, when this discontinuity is realized in a short interval of time (tangential discontinuity in a nozzle, initial regions of a zone of mixing of different flows, etc.), one does not consider it as an admissible discontinuity. This is a manifestation of the limitations imposed by considering "ideal" media or media with a small viscosity, since in an ideal medium the tangential discontinuity is preserved. Therefore the question of the admissibility or non-admissibility of the tangential discontinuity of the flow of an ideal medium has to be analyzed for each separate concrete problem.
Pure contact discontinuities.
Now 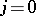 ,
, 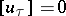 ,
, 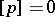 ,
, 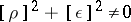 . These may collapse by processes of molecular diffusion; as a rule, these processes are so slow that the contact discontinuity may be regarded as stable over finite intervals of time.
. These may collapse by processes of molecular diffusion; as a rule, these processes are so slow that the contact discontinuity may be regarded as stable over finite intervals of time.
However, a contact discontinuity may also become unstable and rapidly collapse if in the course of a large interval of time the acceleration of the medium on the contact boundary is directed towards the side of the medium with lower density. In this case the contact discontinuity collapses and an "intermixing" of media that were originally on different sides of the contact discontinuity starts. A simple example of a similar, essentially many-dimensional, instability is the collapse in the field of gravity of a horizontal contact discontinuity between a light fluid, found in the lower part of a vessel, in the presence of a much heavier fluid above it (so-called Rayleigh–Taylor instability).
Shock waves.
In this case 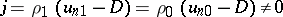 and (1) implies
and (1) implies 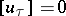 , i.e. the tangential discontinuity of the velocity vector is absent. Condition (1) on the shock wave
, i.e. the tangential discontinuity of the velocity vector is absent. Condition (1) on the shock wave 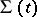 leads to the three equations
leads to the three equations
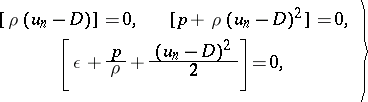 | (2) |
which are called the Rankine–Hugoniot conditions. If 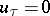 , then the shock wave is called straight, in the opposite case oblique. The elimination of
, then the shock wave is called straight, in the opposite case oblique. The elimination of 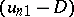 ,
, 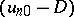 from (2) gives the relation
from (2) gives the relation
 | (3) |
which relates only thermodynamic parameters of the medium on the two sides of the shock wave. This relation is called the adiabatic shock, or the Hugoniot adiabatic.
Let the surface 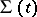 be moving in the direction
be moving in the direction 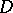 from the left to the right. Then if
from the left to the right. Then if 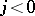 , the shock wave relative to the medium moves to the right, and the matter crosses the shock wave
, the shock wave relative to the medium moves to the right, and the matter crosses the shock wave 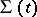 moving relative to
moving relative to 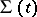 from the right to the left. Conversely, if
from the right to the left. Conversely, if 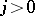 , then the shock wave moves to the left relative to the medium. The medium to the right of the shock wave for
, then the shock wave moves to the left relative to the medium. The medium to the right of the shock wave for 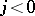 and to the left of the shock wave for
and to the left of the shock wave for 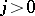 is called the medium in front of the shock wave, the other medium is the medium beyond the shock wave. The parameters of the medium in front of the shock wave are
is called the medium in front of the shock wave, the other medium is the medium beyond the shock wave. The parameters of the medium in front of the shock wave are 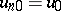 ,
, 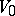 ,
, 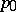 ,
, 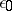 ; the parameters of the medium beyond the shock wave are
; the parameters of the medium beyond the shock wave are 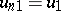 ,
, 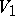 ,
, 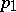 ,
, 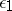 . In the process of motion the part in front of the shock wave passes across the surface
. In the process of motion the part in front of the shock wave passes across the surface 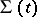 of the shock wave and joins the medium beyond the shock wave
of the shock wave and joins the medium beyond the shock wave 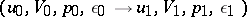 . Moreover, it passes through a zone of high gradients (a shock wave zone) in which one cannot neglect dissipative processes — friction and heat conduction — in spite of small viscosity and thermal conductivity coefficients of the matter. In view of the irreversibility of the dissipative processes, the condition
. Moreover, it passes through a zone of high gradients (a shock wave zone) in which one cannot neglect dissipative processes — friction and heat conduction — in spite of small viscosity and thermal conductivity coefficients of the matter. In view of the irreversibility of the dissipative processes, the condition 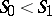 must hold, where
must hold, where 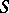 is the entropy of the gas. This inequality does not allow an exchange of states
is the entropy of the gas. This inequality does not allow an exchange of states  ,
, 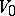 ,
, 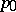 ,
, 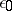 and
and 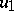 ,
,  ,
,  ,
, 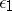 (as is allowed by (2), (3)), but defines the position of these states relative to the surface
(as is allowed by (2), (3)), but defines the position of these states relative to the surface 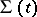 .
.
The condition 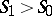 is called the stability condition of the shock wave. The question of the realizability (admissibility) of a shock wave, on which (2), (3) and
is called the stability condition of the shock wave. The question of the realizability (admissibility) of a shock wave, on which (2), (3) and 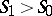 hold, can be solved comparatively simply only for a so-called normal gas. A gas (fluid) is called a normal gas if its equations of state have the form
hold, can be solved comparatively simply only for a so-called normal gas. A gas (fluid) is called a normal gas if its equations of state have the form
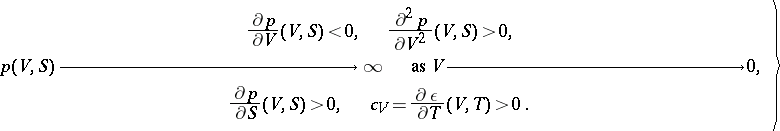 | (4) |
For a normal gas the condition 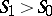 guarantees the stability of the shock wave; from the Hugoniot conditions (2), the state
guarantees the stability of the shock wave; from the Hugoniot conditions (2), the state 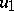 ,
, 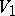 ,
, 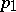 ,
, 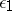 beyond the shock wave front is uniquely determined by the given state
beyond the shock wave front is uniquely determined by the given state 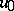 ,
,  ,
, 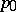 ,
, 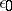 , and the mass flow
, and the mass flow 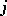 if
if
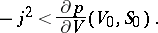 |
From the stability condition 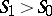 for the shock wave there follow the properties: a) the shock wave moves with supersonic speed through the medium before the front and with subsonic speed through the medium beyond the front (Tsemplen's theorem), i.e.
for the shock wave there follow the properties: a) the shock wave moves with supersonic speed through the medium before the front and with subsonic speed through the medium beyond the front (Tsemplen's theorem), i.e.
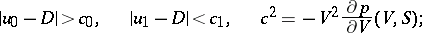 |
b) the shock wave leads to compressed matter and increases the pressure in it, i.e. 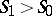 implies
implies 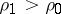 ,
, 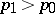 .
.
Adiabatic shock.
For a normal gas the adiabatic shock (3) is represented in the 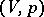 -plane by a curve that is downward convex,
-plane by a curve that is downward convex, 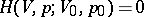 ,
, 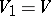 ,
, 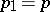 , passing through the point
, passing through the point 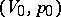 , called the centre of the adiabatic shock. The graph of an adiabatic shock for
, called the centre of the adiabatic shock. The graph of an adiabatic shock for 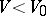 lies above the adiabatic Poisson graph
lies above the adiabatic Poisson graph 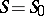 , and lies below it for
, and lies below it for 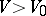 ; at the point
; at the point 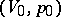 these two adiabatics have contact of at least the second order. The state
these two adiabatics have contact of at least the second order. The state  beyond the front of the shock wave corresponds to the left branch of the adiabatic shock
beyond the front of the shock wave corresponds to the left branch of the adiabatic shock 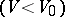 .
.
For a medium with equations of state
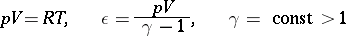 |
(the so-called ideal gas) conditions (4) hold and equation (3) takes the form
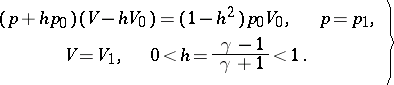 | (5) |
Equation (5) defines a hyperbola with asymptotes 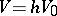 ,
, 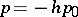 . The limiting compression of the matter is attained behind the infinitely strong shock wave:
. The limiting compression of the matter is attained behind the infinitely strong shock wave:
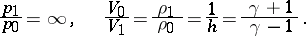 |
The solution of (2) for 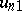 ,
, 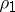 ,
, 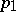 in terms of the given
in terms of the given 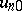 ,
, 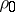 ,
, 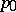 , and
, and 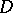 is provided by the formulas
is provided by the formulas
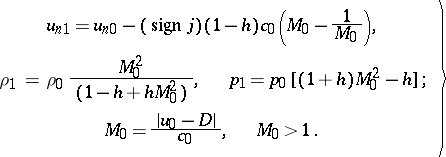 | (6) |
For gases with anomalous thermodynamic properties, when conditions (4) are violated, the requirement 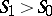 does not guarantee stability (admissibility) of the shock transition. The question of the conditions for the admissibility of a shock transition is very complicated and, for gases with arbitrary equations of state satisfying only the necessary thermodynamic conditions, has not been resolved. The case most studied is that when of the conditions (4) only the condition
does not guarantee stability (admissibility) of the shock transition. The question of the conditions for the admissibility of a shock transition is very complicated and, for gases with arbitrary equations of state satisfying only the necessary thermodynamic conditions, has not been resolved. The case most studied is that when of the conditions (4) only the condition 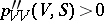 is violated and
is violated and 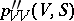 may have alternating sign. In this case the adiabatic shock (3) contains states
may have alternating sign. In this case the adiabatic shock (3) contains states 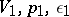 for which the shock transition
for which the shock transition 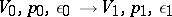 is unstable even when the condition
is unstable even when the condition 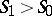 holds.
holds.
The zone of shock transition and its width.
This is the zone of continuous change of the parameters of a medium from its values before the front to its values beyond the shock wave front for real media, having finite viscosity and thermal conductivity. It is assumed here that a continuous transition exists only for stable shock waves. Therefore the study of continuous shock transitions gives admissibility criteria for shock waves. The character of change of the parameters of the medium in the transition zone is also studied.
For a narrow transition zone any shock wave may be considered as locally planar. Therefore the shock transition may be described as the solution of the one-dimensional equations of gas dynamics with plane symmetry for a viscous and thermally-conducting gas:
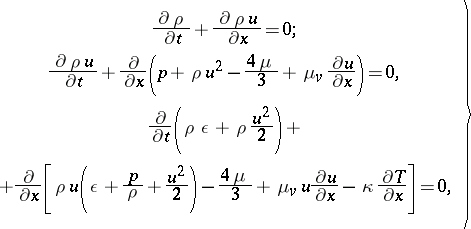 | (7) |
where 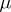 and
and 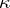 are the viscosity and thermal conductivity coefficients (here assumed to be constant) and
are the viscosity and thermal conductivity coefficients (here assumed to be constant) and 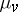 is the bulk viscosity. Equations (7) are supplemented by the equation of state
is the bulk viscosity. Equations (7) are supplemented by the equation of state 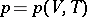 from
from 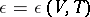 . In a coordinate system moving with the velocity
. In a coordinate system moving with the velocity 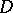 of the shock wave, the shock transition may be described as a stationary solution of equations (7). For these one obtains two equations:
of the shock wave, the shock transition may be described as a stationary solution of equations (7). For these one obtains two equations:
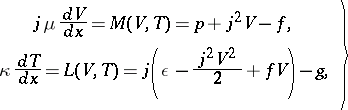 | (8) |
where  ,
, 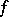 and
and 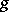 are constant.
are constant.
Equations (8) must be solved by a solution 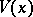 ,
, 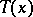 such that
such that 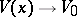 ,
, 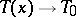 as
as 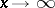 and
and 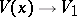 ,
, 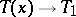 as
as 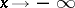 . Necessary conditions for the existence of such a solution,
. Necessary conditions for the existence of such a solution,
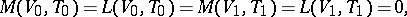 |
reduce to Hugoniot's conditions (2).
A qualitative study of the portrait of the integral curves of the system (8) leads to the conclusion that there exists a unique integral curve for this problem provided conditions (4) are satisfied for the equations of state of the gas; the parameters 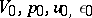 and
and 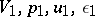 satisfy Hugoniot's conditions; the stability condition for shock waves
satisfy Hugoniot's conditions; the stability condition for shock waves 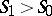 holds. The "width" of the zone of shock transition is infinite and the approximation to the limiting value takes place exponentially. In the case of a non-viscous thermally-conducting gas (
holds. The "width" of the zone of shock transition is infinite and the approximation to the limiting value takes place exponentially. In the case of a non-viscous thermally-conducting gas (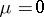 ,
, 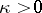 ), which may be considered as the limit
), which may be considered as the limit 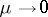 of the general case, there exists a continuous solution of the problem of shock transition if the curve
of the general case, there exists a continuous solution of the problem of shock transition if the curve 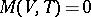 in the plane of the variables
in the plane of the variables 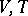 is monotone. In the opposite case (which happens for sufficiently strong shock waves) the limit for
is monotone. In the opposite case (which happens for sufficiently strong shock waves) the limit for 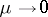 of the integral curves may have density discontinuity at constant temperature (the so-called isothermal jump). This means that the solutions of the equations of gas dynamics for thermally-conducting media without viscosity may be discontinuous. If the medium has viscosity
of the integral curves may have density discontinuity at constant temperature (the so-called isothermal jump). This means that the solutions of the equations of gas dynamics for thermally-conducting media without viscosity may be discontinuous. If the medium has viscosity 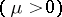 and vanishing thermal conductivity
and vanishing thermal conductivity 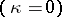 , then there always exists a continuous transition
, then there always exists a continuous transition 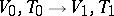 . From this one may conclude that the solutions of the equations of gas dynamics for viscous media cannot have a discontinuity of shock wave type, i.e. for them the Cauchy problem has a global solution (for any
. From this one may conclude that the solutions of the equations of gas dynamics for viscous media cannot have a discontinuity of shock wave type, i.e. for them the Cauchy problem has a global solution (for any 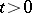 ). However, a rigorous proof of this fact is still lacking.
). However, a rigorous proof of this fact is still lacking.
Similarly one can study shock transitions for an ideal gas:  ,
, 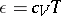 (where
(where 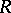 ,
, 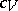 are constants). The equations (8) may in this case be integrated for
are constants). The equations (8) may in this case be integrated for 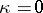 ,
, 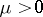 :
:
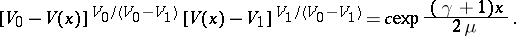 |
The effective width of the zone of shock transition is determined as follows:
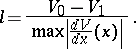 |
A calculation shows that the width 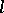 of the shock wave has the order of magnitude of the free path of a molecule.
of the shock wave has the order of magnitude of the free path of a molecule.
This justifies the point of view according to which the flow of a gas is divided into domains of reversible processes, where the flow can be described by the equations of gas dynamics without taking account of dissipative terms, and domains of irreversible processes, represented by narrow zones which may effectively be described by a moving surface of discontinuity (shock wave). More precisely, the behaviour of the parameters of the medium in the zone of shock transition is described by the Boltzmann equation for gas-dynamic processes in non-equilibrium.
For gases with anomalous thermodynamic properties the study of the zone of shock transition is more complicated. The case when 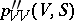 alternates in sign has been analyzed. Let
alternates in sign has been analyzed. Let 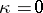 ,
, 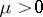 in (8). Then
in (8). Then 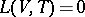 and the determination of
and the determination of 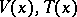 reduces to the solution of a single equation:
reduces to the solution of a single equation:
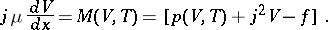 | (9) |
The solution of this equation  ,
, 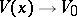 as
as 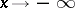 and
and 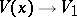 as
as 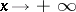 , exists if
, exists if 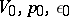 and
and 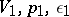 lie on the adiabatic shock (3) and if
lie on the adiabatic shock (3) and if
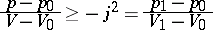 | (10) |
at the points of the curve 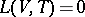 for
for 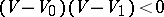 .
.
From (10) it follows that 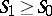 , where if
, where if 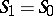 , then the segment of the Hugoniot adiabatic (3) between the points
, then the segment of the Hugoniot adiabatic (3) between the points 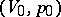 and
and 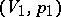 in the plane of the variables
in the plane of the variables 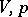 is a segment of the line
is a segment of the line 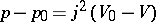 . The inequality (10) gives a condition of admissibility of the shock waves in case
. The inequality (10) gives a condition of admissibility of the shock waves in case 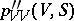 alternates in sign. The basic properties of the shock waves in this case are modified: a)
alternates in sign. The basic properties of the shock waves in this case are modified: a) 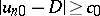 ,
, 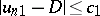 ; and b) the shock waves lead to a non-decreasing entropy
; and b) the shock waves lead to a non-decreasing entropy 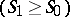 . There exist compressed shock waves
. There exist compressed shock waves 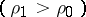 and rarefied shock waves
and rarefied shock waves 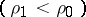 .
.
The origin of shock waves.
In ideal media shock waves are found both as the result of the decomposition of the initial discontinuities into stable discontinuities (shock waves, contact and tangent discontinuities), as well as in the process of flow continuous up to a certain moment. E.g. in a one-dimensional isentropic flow of an ideal gas 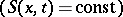 shock waves do not arise if for
shock waves do not arise if for 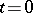 the conditions
the conditions
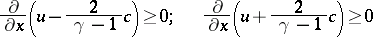 |
hold, and, conversely, shock waves do arise if one of these conditions is violated.
In the theory of discontinuous solutions of quasi-linear hyperbolic equations and systems, a theory of discontinuities has been developed, similar to the mathematical theory of shock waves in gas dynamics. Basic results (far from complete) were obtained only for the case of two independent variables  and
and 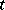 . One quasi-linear equation
. One quasi-linear equation
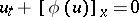 | (11) |
can be considered as a conservation law, so that 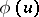 is the flow of the quantity
is the flow of the quantity  . The continuity of the flow through the line of discontinuity
. The continuity of the flow through the line of discontinuity 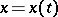 leads to the condition
leads to the condition
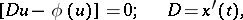 | (12) |
which in analogy to (1) can be called the Hugoniot condition. Like for shock waves in gas dynamics, to (12) one adds the requirement of stability of the discontinuity. This guarantees the uniqueness of the solution of the Cauchy problem for (11) in the class of discontinuous functions. If  and
and 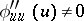 , then the stability condition takes the form
, then the stability condition takes the form
 |
For quasi-linear systems of conservation laws,
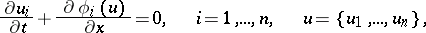 | (13) |
the Hugoniot conditions have the form (12), where 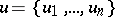 ,
, 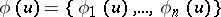 . The problem of finding correct conditions of stability at the discontinuity has been solved only for a restricted class of systems of the form (13).
. The problem of finding correct conditions of stability at the discontinuity has been solved only for a restricted class of systems of the form (13).
References
| [1] | S. Earnshaw, Phil. Trans. Roy. Soc. London , 150 (1860) pp. 133–148 |
| [2] | B. Riemann, "Ueber die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite" , Gesamm. math. Werke , Dover, reprint (1953) pp. 156–175 |
| [3] | W.J.M. Rankine, Phil. Trans. Roy. Soc. London , 160 (1870) pp. 277–288 |
| [4] | H. Hugoniot, J. École Polytechn. , 58 (1889) pp. 1–125 |
| [5] | N.E. Kochin, , Collected works , 2 , Moscow-Leningrad (1949) pp. 5–42 (In Russian) |
| [6] | L.D. Landau, E.M. Lifshitz, "Fluid mechanics" , Pergamon (1959) (Translated from Russian) |
| [7] | H. Weyl, "Shock waves in arbitrary fluids" Comm. Pure Appl. Math. , 2 (1949) pp. 103–122 |
| [8] | D. Gilbarg, "The existence and limit behavior of the one-dimensional shock layer" Amer. J. Math. , 73 (1951) pp. 256–274 |
| [9] | R. Becker, Z. Phys. , 8 (1922) pp. 321–362 |
| [10] | R. Courant, K.O. Friedrichs, "Supersonic flow and shock waves" , Interscience (1948) |
| [11] | L.I. Sedov, "A course in continuum mechanics" , 1–4 , Wolters-Noordhoff (1971–1972) (Translated from Russian) |
| [12] | Ya.B. Zel'dovich, "Theory of combustion and detonation of gases" , Moscow-Leningrad (1944) (In Russian) |
| [13] | B.L. Rozhdestvenskii, N.N. Yanenko, "Systems of quasilinear equations and their applications to gas dynamics" , Amer. Math. Soc. (1983) (Translated from Russian) |
| [14] | O.A. Oleinik, "Discontinuous solutions of non-linear differential equations" Uspekhi Mat. Nauk , 12 : 3 (1957) pp. 3–73 (In Russian) |
Comments
The short sentence concerning the use of the Boltzmann equation to describe the behaviour of the fluid dynamical variables in the zone of shock transition requires some clarification. The problem of the structure of a shock wave has been the subject of many studies [a1]; for weak shocks (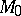 close to 1) the solution of the Boltzmann equation agrees with the solution of the Navier–Stokes equations for compressible fluids, but when
close to 1) the solution of the Boltzmann equation agrees with the solution of the Navier–Stokes equations for compressible fluids, but when 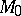 increases (
increases (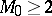 ), the two solutions are widely different.
), the two solutions are widely different.
References
| [a1] | C. Cercignani, "The Boltzmann equation and its applications" , Springer (1988) |
| [a2] | J. Smoller, "Shock waves and reaction-diffusion equations" , Springer (1983) |
Shock waves, mathematical theory of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shock_waves,_mathematical_theory_of&oldid=17631