Difference between revisions of "Shimura variety"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex done) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|done}} | |
| − | + | The family of quotients of a bounded [[Symmetric domain|symmetric domain]] $ X $ | |
| + | by the congruence subgroups of a fixed [[Algebraic group|algebraic group]] $ G $ | ||
| + | acting transitively on $ X $. | ||
| + | Examples include the family of elliptic modular curves (cf. [[Modular curve|Modular curve]]), the family of Hilbert modular varieties corresponding to a fixed totally real field, and the family of Siegel modular varieties of a fixed dimension. The arithmetic properties of Shimura varieties were extensively studied by G. Shimura beginning in the early 1960s. | ||
| − | + | P. Deligne has given a definition according to which a Shimura variety is defined by a reductive algebraic group (cf. also [[Reductive group|Reductive group]]) $ G $ | |
| + | over $ \mathbf Q $ | ||
| + | and a $ G ( \mathbf R ) $- | ||
| + | conjugacy class $ X $ | ||
| + | of homomorphisms $ \mathbf C ^ \times \rightarrow G ( \mathbf R ) $ | ||
| + | satisfying certain axioms sufficient to ensure that $ X $ | ||
| + | is a finite union of bounded symmetric domains [[#References|[a4]]]. The Shimura variety is then the family $$ | ||
| + | { \mathop{\rm Sh}\nolimits} _{K} ( G,X ) = G ( \mathbf Q ) \backslash X \times G ( \mathbf A _{f} ) /K, | ||
| + | $$ | ||
| + | where $ \mathbf A _{f} $ | ||
| + | is the ring of finite adèles of $ \mathbf Q $( | ||
| + | cf. [[Adèle|Adèle]]) and $ K $ | ||
| + | runs through the compact open subgroups of $ G ( \mathbf A _{f} ) $. | ||
| + | Initially, $ { \mathop{\rm Sh}\nolimits} _{K} ( G,X ) $ | ||
| + | is only a [[Complex manifold|complex manifold]], but the Baily–Borel theorem [[#References|[a2]]] endows it with a canonical structure of a quasi-projective [[Algebraic variety|algebraic variety]]. The Shimura varieties of Deligne's definition differ slightly from the earlier examples in that they are families of non-connected varieties. | ||
| − | + | The weight of a Shimura variety is the common reciprocal of the restrictions of the mappings $ \mathbf C ^ \times \rightarrow G ( \mathbf R ) $ | |
| + | in $ X $ | ||
| + | to $ \mathbf R ^ \times $. | ||
| + | When the weight is defined over $ \mathbf Q $, | ||
| + | the Shimura variety may be a moduli variety for Abelian varieties with Hodge class and level structures (Shimura varieties of Hodge type), or Abelian motives with additional structure (Shimura varieties of Abelian type) [[#References|[a4]]], [[#References|[a6]]] (cf. also [[Moduli theory|Moduli theory]]; [[Motives, theory of|Motives, theory of]]). A Shimura variety whose weight is not rational is not a moduli variety, and not every Shimura variety whose weight is rational is known to be a moduli variety. | ||
| − | The | + | The data $ ( G,X ) $ |
| − | + | defining a Shimura variety determine a number field $ E \subset \mathbf C $, | |
| − | + | called the reflex field for the Shimura variety, and every Shimura variety is known to have a canonical model over its reflex field that is characterized by the action of the absolute Galois group (cf. also [[Galois group|Galois group]]) of $ E $ | |
| + | on certain special points of the Shimura variety [[#References|[a4]]], [[#References|[a5]]]. | ||
Holomorphic automorphic forms can be interpreted as the sections of certain vector bundles on Shimura varieties, called automorphic vector bundles, and the arithmetic properties of the automorphic forms are reflected in the arithmetic properties of the corresponding bundles. | Holomorphic automorphic forms can be interpreted as the sections of certain vector bundles on Shimura varieties, called automorphic vector bundles, and the arithmetic properties of the automorphic forms are reflected in the arithmetic properties of the corresponding bundles. | ||
| Line 17: | Line 39: | ||
The study of the boundaries of Shimura varieties suggests the definition of a more general object, that of a mixed Shimura variety, which plays the same role for Fourier–Jacobi series that a Shimura variety plays for holomorphic automorphic forms [[#References|[a5]]], [[#References|[a7]]]. | The study of the boundaries of Shimura varieties suggests the definition of a more general object, that of a mixed Shimura variety, which plays the same role for Fourier–Jacobi series that a Shimura variety plays for holomorphic automorphic forms [[#References|[a5]]], [[#References|[a7]]]. | ||
| − | Roughly speaking, the goal in the study of Shimura varieties is to generalize everything that is known about modular curves to all Shimura varieties. For example, R. Langlands has launched an ambitious program to identify the zeta-function of a Shimura variety with an alternating product of automorphic | + | Roughly speaking, the goal in the study of Shimura varieties is to generalize everything that is known about modular curves to all Shimura varieties. For example, R. Langlands has launched an ambitious program to identify the zeta-function of a Shimura variety with an alternating product of automorphic $ L $- |
| + | functions [[#References|[a3]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Ash, D. Mumford, M. Rapoport, Y. Tai, "Smooth compactification of locally symmetric varieties" , Math. Sci. Press (1975) {{MR|0457437}} {{ZBL|0334.14007}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Baily, A. Borel, "Compactification of arithmetic quotients of bounded symmetric domains" ''Ann. of Math. (2)'' , '''84''' (1966) pp. 442–528 {{MR|0216035}} {{ZBL|0154.08602}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Blasius, J. Rogawski, "Zeta functions of Shimura varieties" U. Jannsen (ed.) S. Kleiman (ed.) J.-P. Serre (ed.) , ''Motives'' , ''Proc. Symp. Pure Math.'' , '''55: 2''' , Amer. Math. Soc. (1994) pp. 525–571 {{MR|1265563}} {{ZBL|0827.11033}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Deligne, "Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques" A. Borel (ed.) W. Casselman (ed.) , ''Automorphic Forms, Representations, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110090/s11009025.png" />-Functions'' , ''Proc. Symp. Pure Math.'' , '''33: 2''' , Amer. Math. Soc. (1979) pp. 247–290 {{MR|0546620}} {{ZBL|0437.14012}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. Milne, "Canonical models of (mixed) Shimura varieties and automorphic vector bundles" , ''Automorphic Forms, Shimura Varieties and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110090/s11009026.png" />-functions'' , ''Perspect. Math.'' , '''10''' , Acad. Press (1990) pp. 283–414 {{MR|1044823}} {{ZBL|0704.14016}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J. Milne, "Shimura varieties and motives" U. Jannsen (ed.) S. Kleiman (ed.) J.-P. Serre (ed.) , ''Motives'' , ''Proc. Symp. Pure Math.'' , '''55: 2''' , Amer. Math. Soc. (1994) pp. 447–523 {{MR|1265562}} {{ZBL|0816.14022}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> R. Pink, "Arithmetical compactification of mixed Shimura varieties" , Bonn (1989) (Dissertation) {{MR|1128753}} {{ZBL|0748.14007}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Ash, D. Mumford, M. Rapoport, Y. Tai, "Smooth compactification of locally symmetric varieties" , Math. Sci. Press (1975) {{MR|0457437}} {{ZBL|0334.14007}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Baily, A. Borel, "Compactification of arithmetic quotients of bounded symmetric domains" ''Ann. of Math. (2)'' , '''84''' (1966) pp. 442–528 {{MR|0216035}} {{ZBL|0154.08602}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Blasius, J. Rogawski, "Zeta functions of Shimura varieties" U. Jannsen (ed.) S. Kleiman (ed.) J.-P. Serre (ed.) , ''Motives'' , ''Proc. Symp. Pure Math.'' , '''55: 2''' , Amer. Math. Soc. (1994) pp. 525–571 {{MR|1265563}} {{ZBL|0827.11033}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Deligne, "Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques" A. Borel (ed.) W. Casselman (ed.) , ''Automorphic Forms, Representations, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110090/s11009025.png" />-Functions'' , ''Proc. Symp. Pure Math.'' , '''33: 2''' , Amer. Math. Soc. (1979) pp. 247–290 {{MR|0546620}} {{ZBL|0437.14012}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. Milne, "Canonical models of (mixed) Shimura varieties and automorphic vector bundles" , ''Automorphic Forms, Shimura Varieties and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110090/s11009026.png" />-functions'' , ''Perspect. Math.'' , '''10''' , Acad. Press (1990) pp. 283–414 {{MR|1044823}} {{ZBL|0704.14016}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J. Milne, "Shimura varieties and motives" U. Jannsen (ed.) S. Kleiman (ed.) J.-P. Serre (ed.) , ''Motives'' , ''Proc. Symp. Pure Math.'' , '''55: 2''' , Amer. Math. Soc. (1994) pp. 447–523 {{MR|1265562}} {{ZBL|0816.14022}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> R. Pink, "Arithmetical compactification of mixed Shimura varieties" , Bonn (1989) (Dissertation) {{MR|1128753}} {{ZBL|0748.14007}} </TD></TR></table> | ||
Revision as of 20:39, 21 December 2019
The family of quotients of a bounded symmetric domain $ X $
by the congruence subgroups of a fixed algebraic group $ G $
acting transitively on $ X $.
Examples include the family of elliptic modular curves (cf. Modular curve), the family of Hilbert modular varieties corresponding to a fixed totally real field, and the family of Siegel modular varieties of a fixed dimension. The arithmetic properties of Shimura varieties were extensively studied by G. Shimura beginning in the early 1960s.
P. Deligne has given a definition according to which a Shimura variety is defined by a reductive algebraic group (cf. also Reductive group) $ G $ over $ \mathbf Q $ and a $ G ( \mathbf R ) $- conjugacy class $ X $ of homomorphisms $ \mathbf C ^ \times \rightarrow G ( \mathbf R ) $ satisfying certain axioms sufficient to ensure that $ X $ is a finite union of bounded symmetric domains [a4]. The Shimura variety is then the family $$ { \mathop{\rm Sh}\nolimits} _{K} ( G,X ) = G ( \mathbf Q ) \backslash X \times G ( \mathbf A _{f} ) /K, $$ where $ \mathbf A _{f} $ is the ring of finite adèles of $ \mathbf Q $( cf. Adèle) and $ K $ runs through the compact open subgroups of $ G ( \mathbf A _{f} ) $. Initially, $ { \mathop{\rm Sh}\nolimits} _{K} ( G,X ) $ is only a complex manifold, but the Baily–Borel theorem [a2] endows it with a canonical structure of a quasi-projective algebraic variety. The Shimura varieties of Deligne's definition differ slightly from the earlier examples in that they are families of non-connected varieties.
The weight of a Shimura variety is the common reciprocal of the restrictions of the mappings $ \mathbf C ^ \times \rightarrow G ( \mathbf R ) $ in $ X $ to $ \mathbf R ^ \times $. When the weight is defined over $ \mathbf Q $, the Shimura variety may be a moduli variety for Abelian varieties with Hodge class and level structures (Shimura varieties of Hodge type), or Abelian motives with additional structure (Shimura varieties of Abelian type) [a4], [a6] (cf. also Moduli theory; Motives, theory of). A Shimura variety whose weight is not rational is not a moduli variety, and not every Shimura variety whose weight is rational is known to be a moduli variety.
The data $ ( G,X ) $ defining a Shimura variety determine a number field $ E \subset \mathbf C $, called the reflex field for the Shimura variety, and every Shimura variety is known to have a canonical model over its reflex field that is characterized by the action of the absolute Galois group (cf. also Galois group) of $ E $ on certain special points of the Shimura variety [a4], [a5].
Holomorphic automorphic forms can be interpreted as the sections of certain vector bundles on Shimura varieties, called automorphic vector bundles, and the arithmetic properties of the automorphic forms are reflected in the arithmetic properties of the corresponding bundles.
The Baily–Borel theorem provides a canonical compactification of a Shimura variety that is minimal in a certain sense, but which is usually highly singular. The theory of toroidal imbeddings provides compactifications that are both projective and smooth, but not canonical [a1].
The study of the boundaries of Shimura varieties suggests the definition of a more general object, that of a mixed Shimura variety, which plays the same role for Fourier–Jacobi series that a Shimura variety plays for holomorphic automorphic forms [a5], [a7].
Roughly speaking, the goal in the study of Shimura varieties is to generalize everything that is known about modular curves to all Shimura varieties. For example, R. Langlands has launched an ambitious program to identify the zeta-function of a Shimura variety with an alternating product of automorphic $ L $- functions [a3].
References
| [a1] | A. Ash, D. Mumford, M. Rapoport, Y. Tai, "Smooth compactification of locally symmetric varieties" , Math. Sci. Press (1975) MR0457437 Zbl 0334.14007 |
| [a2] | W. Baily, A. Borel, "Compactification of arithmetic quotients of bounded symmetric domains" Ann. of Math. (2) , 84 (1966) pp. 442–528 MR0216035 Zbl 0154.08602 |
| [a3] | D. Blasius, J. Rogawski, "Zeta functions of Shimura varieties" U. Jannsen (ed.) S. Kleiman (ed.) J.-P. Serre (ed.) , Motives , Proc. Symp. Pure Math. , 55: 2 , Amer. Math. Soc. (1994) pp. 525–571 MR1265563 Zbl 0827.11033 |
| [a4] | P. Deligne, "Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques" A. Borel (ed.) W. Casselman (ed.) , Automorphic Forms, Representations, and 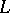 -Functions , Proc. Symp. Pure Math. , 33: 2 , Amer. Math. Soc. (1979) pp. 247–290 MR0546620 Zbl 0437.14012 -Functions , Proc. Symp. Pure Math. , 33: 2 , Amer. Math. Soc. (1979) pp. 247–290 MR0546620 Zbl 0437.14012 |
| [a5] | J. Milne, "Canonical models of (mixed) Shimura varieties and automorphic vector bundles" , Automorphic Forms, Shimura Varieties and 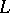 -functions , Perspect. Math. , 10 , Acad. Press (1990) pp. 283–414 MR1044823 Zbl 0704.14016 -functions , Perspect. Math. , 10 , Acad. Press (1990) pp. 283–414 MR1044823 Zbl 0704.14016 |
| [a6] | J. Milne, "Shimura varieties and motives" U. Jannsen (ed.) S. Kleiman (ed.) J.-P. Serre (ed.) , Motives , Proc. Symp. Pure Math. , 55: 2 , Amer. Math. Soc. (1994) pp. 447–523 MR1265562 Zbl 0816.14022 |
| [a7] | R. Pink, "Arithmetical compactification of mixed Shimura varieties" , Bonn (1989) (Dissertation) MR1128753 Zbl 0748.14007 |
Shimura variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shimura_variety&oldid=44316