Shimura correspondence
By a modular form of weight  one understands a function
one understands a function  on the upper half-plane satisfying
on the upper half-plane satisfying  for some suitable function
for some suitable function  when
when
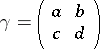 |
is an element of some congruence subgroup of  (cf. also Modular function).
(cf. also Modular function).
If  is an integer, E. Hecke defined operators
is an integer, E. Hecke defined operators  for every integer
for every integer  , and showed they could be simultaneously diagonalizable (cf. also Hecke operator). The
, and showed they could be simultaneously diagonalizable (cf. also Hecke operator). The  -series of a simultaneous eigenfunction (cf. also Dirichlet
-series of a simultaneous eigenfunction (cf. also Dirichlet  -function) is then an Euler product.
-function) is then an Euler product.
Modular forms of half-integral weight arise naturally, for example as theta-series. A theta-series in  variables is a modular form of weight
variables is a modular form of weight  .
.
If  is a half-integer,
is a half-integer, 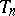 can only be defined if
can only be defined if  is a square on forms of weight
is a square on forms of weight 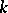 , and there is not enough information in the Hecke eigenvalues to determine the Fourier coefficients. The coefficients are not multiplicative, so the
, and there is not enough information in the Hecke eigenvalues to determine the Fourier coefficients. The coefficients are not multiplicative, so the  -series is not an Euler product.
-series is not an Euler product.
Using the Rankin–Selberg method and a converse theorem, G. Shimura [a1] showed that if  is a modular form of weight
is a modular form of weight  , then there is a corresponding modular form of weight
, then there is a corresponding modular form of weight  such that the
such that the 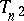 Hecke eigenvalue on
Hecke eigenvalue on 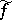 agrees with the
agrees with the 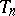 Hecke eigenvalue of
Hecke eigenvalue of  .
.
This result was complemented by the important theorem of J.-L. Waldspurger [a2], showing that the  th Fourier coefficient of
th Fourier coefficient of  agrees with
agrees with  . Waldspurger also gave interpretations of these special values as periods of
. Waldspurger also gave interpretations of these special values as periods of  (integrals over over geodesics). W. Kohnen and D. Zagier [a3] gave a particularly useful treatment of a special case. Also useful is [a4]. P. Sarnak and S. Katok [a5] found similar results for Maass forms.
(integrals over over geodesics). W. Kohnen and D. Zagier [a3] gave a particularly useful treatment of a special case. Also useful is [a4]. P. Sarnak and S. Katok [a5] found similar results for Maass forms.
Given Waldspurger's theorem, the case where  becomes particularly interesting, since if
becomes particularly interesting, since if  is the modular form of weight two associated with an elliptic curve,
is the modular form of weight two associated with an elliptic curve,  has an interpretation in terms of the Birch–Swinnerton-Dyer conjecture. The period interpretation of the special values is then connected with the work of B.H. Gross, Kohnen and Zagier [a6] on heights of Heegner points. A beautiful application of this connection with the Birch–Swinnerton-Dyer conjecture to the classical problem of computing the set of areas of rational right triangles was given in [a7].
has an interpretation in terms of the Birch–Swinnerton-Dyer conjecture. The period interpretation of the special values is then connected with the work of B.H. Gross, Kohnen and Zagier [a6] on heights of Heegner points. A beautiful application of this connection with the Birch–Swinnerton-Dyer conjecture to the classical problem of computing the set of areas of rational right triangles was given in [a7].
An interesting approach to the Shimura correspondence and Waldspurger's theorem is offered by the theory of Jacobi forms, in which both  and its correspondent
and its correspondent  may be related to automorphic forms on the Jacobi group. See [a8] and [a9]; cf. also Automorphic form.
may be related to automorphic forms on the Jacobi group. See [a8] and [a9]; cf. also Automorphic form.
A. Weil realized that (Siegel) modular forms, particularly theta-series, should be interpreted as automorphic forms not on 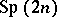 , but on a certain double cover
, but on a certain double cover  , the so-called metaplectic group. If
, the so-called metaplectic group. If  , then
, then  , and this is the proper framework for understanding the classical Shimura correspondence, which can be regarded as a lifting from either
, and this is the proper framework for understanding the classical Shimura correspondence, which can be regarded as a lifting from either  to
to 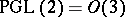 , or from
, or from  to
to 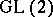 .
.
T. Kubota and K. Matsumoto constructed metaplectic covers of more general groups, provided the ground field contains sufficiently many roots of unity. The Shimura correspondence in this context is a lifting from automorphic forms on the covering group to automorphic forms on 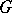 or (sometimes) its dual, obtained by reversing the long and short roots and interchanging the fundamental group with the dual of the centre. See [a10], [a11], [a12], [a13], [a14] for the Shimura correspondence on higher covers of higher rank groups. Finding analogues of Waldspurger's theorem in this context is an important open problem (as of 2000).
or (sometimes) its dual, obtained by reversing the long and short roots and interchanging the fundamental group with the dual of the centre. See [a10], [a11], [a12], [a13], [a14] for the Shimura correspondence on higher covers of higher rank groups. Finding analogues of Waldspurger's theorem in this context is an important open problem (as of 2000).
References
| [a1] | G. Shimura, "On modular forms of half integral weight" Ann. of Math. , 97 (1973) pp. 440–481 |
| [a2] | J.-L. Waldspurger, "Sur les coefficients de Fourier des formes modulaires de poids demi-entier" J. Math. Pures Appl. , 60 (1981) pp. 375–484 |
| [a3] | W. Kohnen, D. Zagier, "Values of 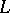 -series of modular forms at the center of the critical strip" Invent. Math. , 64 (1981) pp. 175–198 -series of modular forms at the center of the critical strip" Invent. Math. , 64 (1981) pp. 175–198 |
| [a4] | I. Piatetski–Shapiro, "Work of Waldspurger" , Lie Group Representations II , Lecture Notes in Mathematics , 1041 , Springer (1984) |
| [a5] | P. Sarnak, S. Katok, "Heegner points, cycles and Maass forms" Israel J. Math. , 84 (1993) pp. 193–227 |
| [a6] | B.H. Gross, W. Kohnen, D. Zagier, "Heegner points and derivatives of 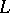 -series II" Math. Ann. , 278 (1987) pp. 497–562 -series II" Math. Ann. , 278 (1987) pp. 497–562 |
| [a7] | J.B. Tunnell, "A classical Diophantine problem and modular forms of weight 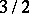 " Invent. Math. , 72 (1983) pp. 323–334 " Invent. Math. , 72 (1983) pp. 323–334 |
| [a8] | M. Eichler, D. Zagier, "Jacobi forms" , Birkhäuser (1985) |
| [a9] | D. Ginzburg, S. Rallis, D. Soudry, "A new construction of the inverse Shimura correspondence" Internat. Math. Res. Notices , 7 (1997) pp. 349–357 |
| [a10] | D. Kazhdan, S.J. Patterson, "Towards a generalized Shimura correspondence" Adv. Math. , 60 (1986) pp. 161–234 |
| [a11] | Y.Z. Flicker, "Automorphic forms on covering groups of 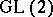 " Invent. Math. , 57 : 2 (1980) pp. 119–182 " Invent. Math. , 57 : 2 (1980) pp. 119–182 |
| [a12] | Y.Z. Flicker, D. Kazhdan, "Metaplectic correspondence" Publ. Math. IHES , 64 (1986) pp. 53–110 |
| [a13] | D. Bump, J. Hoffstein, "On Shimura's correspondence" Duke Math. J. , 55 (1987) pp. 661–691 |
| [a14] | D. Savin, "Local Shimura correspondence" Math. Ann. , 280 (1988) pp. 185–190 |
Shimura correspondence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shimura_correspondence&oldid=15178