Difference between revisions of "Series"
m (→Simple series of numbers.: tex) |
|||
| Line 4: | Line 4: | ||
==Simple series of numbers.== | ==Simple series of numbers.== | ||
| − | A pair of sequences of complex numbers | + | A pair of sequences of complex numbers $\{a_n\}$ and $\{s_n \}$ such that |
| − | + | \begin{equation}\label{eq:1} | |
| − | + | s_n = a_1+\dots+a_n, \quad n=1,2,\dots, | |
| − | + | \end{equation} | |
is called a (simple) series of numbers and is denoted as follows: | is called a (simple) series of numbers and is denoted as follows: | ||
Revision as of 03:34, 30 July 2013
infinite sum
A sequence of elements (called the terms of the given series) of some linear topological space and a certain infinite set of their partial sums (called the partial sums of the series) for which the notion of a limit is defined. Here are the simplest examples of series.
Simple series of numbers.
A pair of sequences of complex numbers $\{a_n\}$ and $\{s_n \}$ such that \begin{equation}\label{eq:1} s_n = a_1+\dots+a_n, \quad n=1,2,\dots, \end{equation} is called a (simple) series of numbers and is denoted as follows:
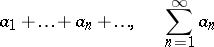 |
or
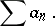 | (2) |
The elements of the sequence 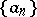 are called the terms of the series and the elements of
are called the terms of the series and the elements of 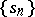 are called its partial sums; moreover,
are called its partial sums; moreover, 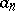 is called the
is called the  -th term of the series (2), and
-th term of the series (2), and 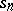 its partial sum of order
its partial sum of order  . The series (2) is defined uniquely by each of the two sequences
. The series (2) is defined uniquely by each of the two sequences 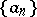 and
and 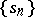 : the terms of the sequence
: the terms of the sequence 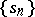 are obtained from the terms of the sequence
are obtained from the terms of the sequence 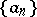 by formula (1), and the sequence
by formula (1), and the sequence 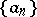 can be recovered from
can be recovered from 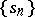 by the formulas
by the formulas
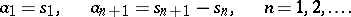 |
From this point of view the study of series is equivalent to the study of sequences: For any statement about series one can formulate an equivalent statement about sequences.
A series (2) is called convergent if the sequence of its partial sums 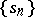 has a finite limit
has a finite limit
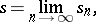 |
which is called the sum of the series (2) and is written as
 |
Thus, the notation (2) is used both for the series itself and for its sum. If the sequence of partial sums of the series (2) does not have a finite limit, then the series is called divergent (cf. also Divergent series).
An example of a convergent series is the sum of the terms of an infinite geometric progression
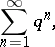 | (3) |
provided that 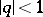 . In this case its sum is equal to
. In this case its sum is equal to 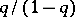 , i.e.
, i.e. 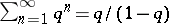 . If
. If 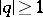 , (3) is an example of a divergent series.
, (3) is an example of a divergent series.
If the series (2) is convergent, then the sequence of terms tends to zero:
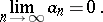 |
The converse of this statement is not true: The sequence 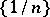 of terms of the harmonic series
of terms of the harmonic series
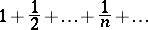 |
tends to zero though this series is divergent.
The series 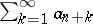 is called the remainder of order
is called the remainder of order  of the series (2). If a series is convergent, then each remainder of it is convergent. If some remainder of a series is convergent, then the series itself is convergent. If the remainder of order
of the series (2). If a series is convergent, then each remainder of it is convergent. If some remainder of a series is convergent, then the series itself is convergent. If the remainder of order  of the series (2) is convergent and its sum is equal to
of the series (2) is convergent and its sum is equal to 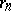 , that is,
, that is, 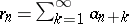 , then
, then
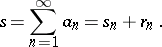 |
If the series (2) and the series
 | (4) |
are convergent, then the series
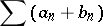 |
is also convergent; this series is called the sum of the series (2) and (4); moreover, its sum is equal to the sum of these series.
If the series (2) is convergent and 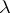 is a complex number, then the series
is a complex number, then the series 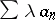 , called the product of the series (2) and the number
, called the product of the series (2) and the number 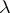 , is also convergent, and
, is also convergent, and 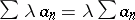 .
.
A condition for the convergence of a series which does not use the notion of its sum is the Cauchy criterion for the convergence of a series.
If all terms of the series (2) are real numbers, 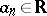 , then the series (2) is called real. In the theory of series an important role is played by real series with non-negative terms:
, then the series (2) is called real. In the theory of series an important role is played by real series with non-negative terms:
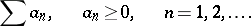 | (5) |
A necessary and sufficient condition for the convergence of the series (5) is that the sequence of its partial sums is bounded above. If this series is divergent, then its partial sums tend to infinity:
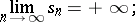 |
therefore, in this case one writes
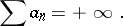 |
For series with non-negative terms there exist quite a number of convergence criteria. The following criteria are the principal ones.
The comparison test. If for a series (5) and for a series
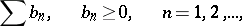 | (6) |
with non-negative terms there exists a constant 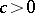 such that
such that 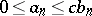 , then the convergence of the series (6) implies the convergence of the series (5), and the divergence of (5) implies the divergence of (6).
, then the convergence of the series (6) implies the convergence of the series (5), and the divergence of (5) implies the divergence of (6).
When the comparison test is applied in studies of the convergence for a given series with non-negative terms, it is often reasonable to single out the principal part of its  -th term with respect to
-th term with respect to 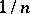 as
as 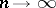 in the form
in the form 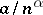 (
( is some constant), and to take the series
is some constant), and to take the series
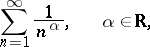 | (7) |
as a comparison series. This series is convergent for 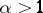 and divergent for
and divergent for 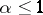 .
.
The rule below follows from the comparison test in case one takes the series (7) as a comparison series: If
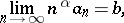 |
then for 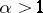 and
and 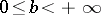 the series (5) converges, and for
the series (5) converges, and for  and
and 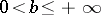 the series (5) diverges.
the series (5) diverges.
The comparison test also implies the d'Alembert criterion (convergence of series) and the Cauchy criterion for the convergence of a series of positive numbers. For such series there also exist the criteria of Bertrand, Gauss, Lobachevskii, Ermakov, Kummer, and Raabe (cf. Bertrand criterion; Gauss criterion; Lobachevskii criterion; Ermakov criterion; Kummer criterion; and Raabe criterion).
The integral test for convergence provides sufficient conditions for the convergence of a series (5) with non-negative terms forming a decreasing sequence: 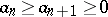 ,
, 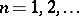 . Let a series (5) be such that there exists a function
. Let a series (5) be such that there exists a function  , defined and decreasing for
, defined and decreasing for 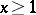 , the values of which on the integers coincide with the terms of the given series:
, the values of which on the integers coincide with the terms of the given series: 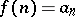 ,
, 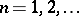 . Then, if
. Then, if 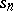 are the partial sums and
are the partial sums and  are the remainders of (5), the following estimates are valid:
are the remainders of (5), the following estimates are valid:
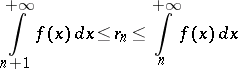 |
and
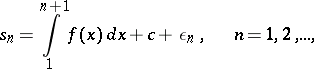 |
where  is some constant and
is some constant and 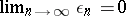 .
.
Thus, the series (5) converges if and only if the integral 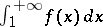 is convergent.
is convergent.
If the series (5) is divergent, then its partial sums 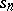 increase in the same way as the integrals
increase in the same way as the integrals 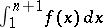 , i.e. the
, i.e. the 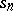 are asymptotically equal to the indicated integrals:
are asymptotically equal to the indicated integrals:
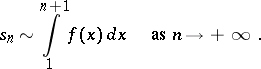 |
For a series (5) whose terms form a decreasing sequence the following Cauchy condensation theorem is valid: If the terms of (5) decrease, then it converges or diverges simultaneously with the series
 |
A necessary condition for the convergence of a series (5) with a decreasing sequence of terms is the condition
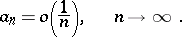 | (8) |
The example of the divergent series
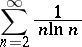 |
shows that condition (8) is not sufficient for the convergence of a series (5) with a decreasing sequence of terms.
An important class of series of numbers are the absolutely convergent series, i.e. series (2) for which the series 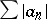 are convergent. If a series is absolutely convergent, then it is convergent and its sum is independent of the order in which the summands are written. Series that are convergent but not absolutely convergent are called conditionally convergent. An example of a conditionally convergent series is the series
are convergent. If a series is absolutely convergent, then it is convergent and its sum is independent of the order in which the summands are written. Series that are convergent but not absolutely convergent are called conditionally convergent. An example of a conditionally convergent series is the series
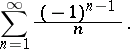 |
The sum of a conditionally convergent series depends on the order in which its terms are written (see Riemann theorem on the rearrangement of the terms of a series): Whatever 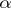 and
and 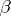 belonging to the set of real numbers completed by the infinities
belonging to the set of real numbers completed by the infinities 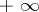 and
and  ,
, 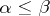 , one can rearrange the terms of any conditionally convergent series with real numbers as its terms so that for the partial sums
, one can rearrange the terms of any conditionally convergent series with real numbers as its terms so that for the partial sums 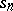 of the resulting series the following equalities will hold:
of the resulting series the following equalities will hold:
 |
Thus, for conditionally convergent series the commutative law of addition is not valid. Also, the associative law of addition does not hold for all series: If a series is divergent, then a series obtained from it by a sequential grouping of terms can be convergent; moreover, its sum depends on the way of grouping the terms of the original series. For example, the series
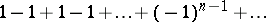 |
is divergent, but the series 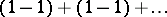 and
and 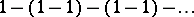 obtained from it by pairwise grouping of its terms are convergent and have different sums. However, if a series is convergent, then, of course, any series obtained from it by a sequential grouping of its terms is convergent and its sum is the sum of the given series, since the sequence of partial sums of the new series is a subsequence of the sequence of partial sums of the original series.
obtained from it by pairwise grouping of its terms are convergent and have different sums. However, if a series is convergent, then, of course, any series obtained from it by a sequential grouping of its terms is convergent and its sum is the sum of the given series, since the sequence of partial sums of the new series is a subsequence of the sequence of partial sums of the original series.
Among the series with terms of different signs it is usual to single out the alternating series for which the Leibniz criterion for convergence is valid. Different criteria for the convergence of arbitrary series of numbers can be obtained by the Abel transformation of the sums of pairwise products, for example, the Abel criterion; the Dedekind criterion (convergence of series); the Dirichlet criterion (convergence of series); and the du Bois-Reymond criterion (convergence of series).
Multiplication of series. There are different rules for the multiplication of series. The best known is Cauchy's rule, according to which to multiply two series (2) and (4) one sums at first in finite "diagonals" the pairwise products  , i.e. the products in which the sum of indices
, i.e. the products in which the sum of indices 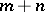 has the same value:
has the same value:
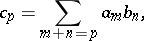 | (9) |
and the series 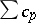 for which the obtained sums are the terms is called the Cauchy product of the two given series. This rule of multiplication of series is suggested by the formula for multiplication of power series:
for which the obtained sums are the terms is called the Cauchy product of the two given series. This rule of multiplication of series is suggested by the formula for multiplication of power series:
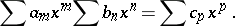 |
Let the series (2), (4) and (9) be convergent and let
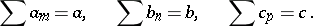 |
If the series (2) and (4) are absolutely convergent, then the series (9) is also absolutely convergent and 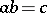 . If the series (2) is absolutely convergent and the series (4) is convergent, then (9) is convergent and
. If the series (2) is absolutely convergent and the series (4) is convergent, then (9) is convergent and 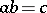 (Mertens' theorem). If the series (2) and (4) are conditionally convergent, then (9) may be divergent; for example, the series
(Mertens' theorem). If the series (2) and (4) are conditionally convergent, then (9) may be divergent; for example, the series
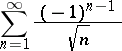 |
is conditionally convergent and the series
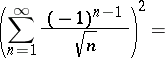 |
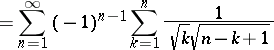 |
is divergent (its terms do not tend to 0). If all three series — (2), (4) and (9) — are convergent, then 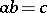 (Abel's product theorem).
(Abel's product theorem).
An example of another rule of multiplication of series is the rule in which at first one carries out the summation of the pairwise products 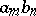 in which the product
in which the product 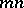 of the indices has a fixed value:
of the indices has a fixed value:
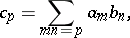 |
then the product of the series (2) and (4) is defined as the series 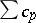 . This rule of multiplication is suggested by the formula for multiplication of Dirichlet series:
. This rule of multiplication is suggested by the formula for multiplication of Dirichlet series:
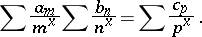 |
There also exist series with terms  numbered by all integers
numbered by all integers 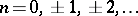 . They are denoted by
. They are denoted by
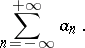 | (10) |
A series (10) is called convergent if the series
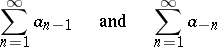 |
are both convergent and the sum of the sums of these two series is called the sum of (10).
Series of numbers of a more complicated structure are multiple series, which have terms 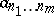 provided with multi-indices, where the
provided with multi-indices, where the 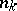 are positive integers,
are positive integers, 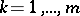 ;
; 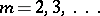 . In the theory of multiple series various types of partial sums are considered: triangular
. In the theory of multiple series various types of partial sums are considered: triangular
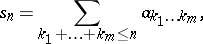 |
rectangular
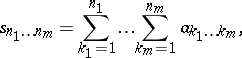 |
spherical
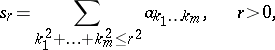 |
and others. According to the chosen type of partial sums one can define the notion of the sum of a multiple series as their corresponding limit. In the case when 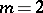 , a multiple series is called a double series. For multiple series, unlike simple series, the given set of partial sums does not determine the terms of a series, i.e. in general, to define a multiple series it is necessary that both the multiple sequence of its terms and the set of its partial sums be given.
, a multiple series is called a double series. For multiple series, unlike simple series, the given set of partial sums does not determine the terms of a series, i.e. in general, to define a multiple series it is necessary that both the multiple sequence of its terms and the set of its partial sums be given.
In mathematical analysis both convergent and divergent series are used. For the latter various methods of summation are worked out.
Many important irrational constants can be obtained as sums of series of numbers, for example:
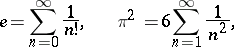 |
the same is true for the values of definite integrals in which the primitives of the integrands cannot be written in elementary functions:
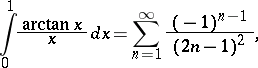 |
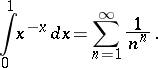 |
Series of functions.
A (simple) series of functions
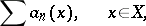 | (11) |
is a pair of sequences of functions 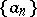 and
and  consisting of numerical functions defined on some set
consisting of numerical functions defined on some set  and such that
and such that
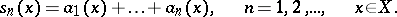 |
As in the case of series of numbers, the elements of the sequence 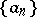 are called the terms of the series (11) and those of the sequence
are called the terms of the series (11) and those of the sequence 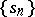 — its partial sums. The series (11) is called convergent on the set
— its partial sums. The series (11) is called convergent on the set 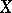 if for each fixed
if for each fixed 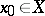 the following series of numbers is convergent:
the following series of numbers is convergent:
 |
Example. The series
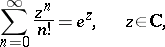 |
is convergent on the entire complex plane 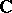 and the series
and the series
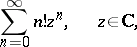 |
only when 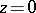 .
.
The sum of a convergent series of functions continuous, for example, on some interval is not necessarily a continuous function; for example, the series
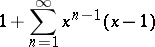 |
is convergent on the interval 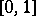 , its terms are continuous on this interval but the sum
, its terms are continuous on this interval but the sum
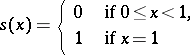 |
is discontinuous at the point 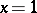 . A number of conditions under which the properties of continuity, differentiability and integrability of finite sums of, respectively, continuous, differentiable or integrable functions can be carried over to series of functions are formulated in terms of uniform convergence of a series (see Uniformly-convergent series).
. A number of conditions under which the properties of continuity, differentiability and integrability of finite sums of, respectively, continuous, differentiable or integrable functions can be carried over to series of functions are formulated in terms of uniform convergence of a series (see Uniformly-convergent series).
Series of measurable functions. Let 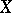 be a Lebesgue-measurable subset of the
be a Lebesgue-measurable subset of the  -dimensional Euclidean space
-dimensional Euclidean space 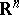 , let
, let 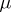 be the Lebesgue measure and let the terms
be the Lebesgue measure and let the terms 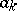 of the series
of the series
 | (12) |
be measurable, almost-everywhere finite functions on 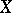 taking values in the extended real line (i.e. together with real numbers they can assume the values
taking values in the extended real line (i.e. together with real numbers they can assume the values 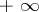 and
and 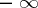 ). If the series (12) is convergent almost-everywhere on
). If the series (12) is convergent almost-everywhere on 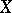 , then its sum
, then its sum  is also a measurable function, and by Egorov's theorem (cf. Egorov theorem), if
is also a measurable function, and by Egorov's theorem (cf. Egorov theorem), if 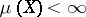 , then for any
, then for any  there exists a compact set
there exists a compact set 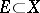 such that
such that 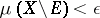 and such that the series with as terms the restrictions
and such that the series with as terms the restrictions 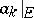 of the functions
of the functions 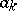 to
to 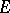 converges uniformly on
converges uniformly on 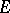 and its sum is
and its sum is 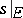 — the restriction of the sum (12) to
— the restriction of the sum (12) to 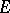 .
.
Let 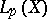 ,
, 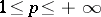 , be the space of functions
, be the space of functions 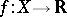 with the norm
with the norm
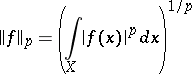 |
for 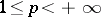 and with the norm
and with the norm
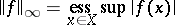 |
for 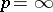 , respectively. A series (12) is called convergent in
, respectively. A series (12) is called convergent in 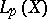 if the sequence of its partial sums
if the sequence of its partial sums 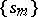 converges in
converges in 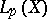 , and its limit
, and its limit  is called the sum of (12) in this space:
is called the sum of (12) in this space:
 |
If a series (12) converges in  and
and  is its sum, then there exists a subsequence of the sequence of its partial sums which converges to
is its sum, then there exists a subsequence of the sequence of its partial sums which converges to  almost-everywhere on
almost-everywhere on 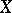 .
.
Term-by-term integration of series. The following theorems are extensions of the theorem on term-by-term integration of uniformly-convergent series.
Theorem 1. If there exists a summable function 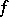 on the set
on the set 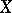 such that for all
such that for all 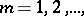 and all
and all  the partial sums
the partial sums 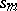 of the series (12) satisfy the inequality
of the series (12) satisfy the inequality
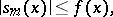 |
if the series (12) converges almost-everywhere on 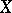 and if its sum is
and if its sum is  , then
, then
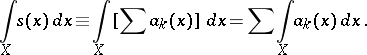 | (13) |
Theorem 2. If 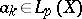 ,
, 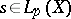 ,
, 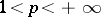 ,
, 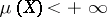 , and if the sequence of partial sums
, and if the sequence of partial sums 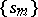 of the series (12) converges weakly to the function
of the series (12) converges weakly to the function  (i.e. for any function
(i.e. for any function 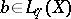 ,
, 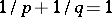 , the following condition is satisfied:
, the following condition is satisfied:
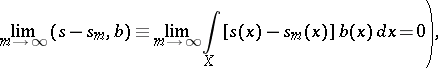 |
then formula (13) holds.
One can also carry out term-by-term integration of a series (12) all terms of which are non-negative on the set 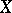 . For such a series the sequence of their partial sums at each point
. For such a series the sequence of their partial sums at each point 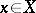 increases and thus has a finite or infinite limit, which is called the value of the sum
increases and thus has a finite or infinite limit, which is called the value of the sum  of the series at this point.
of the series at this point.
Theorem 3. If the terms of (12) are non-negative, then formula (13) holds.
Under the assumptions of theorem 3 both sides of formula (13) can be 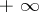 . The following theorem provides sufficient conditions for their finiteness.
. The following theorem provides sufficient conditions for their finiteness.
Theorem 4. If the terms of (12) are non-negative and if the integrals of their partial sums 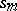 are uniformly bounded:
are uniformly bounded:
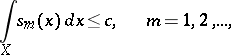 |
where  is a constant, then the sum
is a constant, then the sum  of the series (12) is a summable function.
of the series (12) is a summable function.
Term-by-term differentiation of series. Let 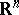 be the
be the  -dimensional Euclidean space of points
-dimensional Euclidean space of points 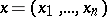 ,
, 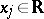 , let
, let 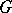 be an open set in
be an open set in 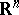 , and
, and 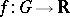 . Let
. Let 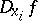 be the generalized derivative of the function
be the generalized derivative of the function 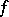 with respect to
with respect to 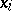 ,
, 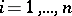 . If
. If  ,
, 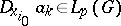 (
(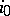 is fixed),
is fixed), 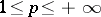 , and if the series
, and if the series 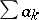 and
and 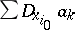 , are convergent in
, are convergent in 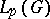 :
: 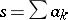 and
and 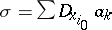 , then
, then  has a generalized derivative in
has a generalized derivative in 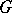 with respect to
with respect to 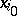 and
and 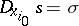 , i.e.
, i.e.
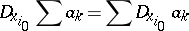 |
in 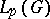 .
.
Among series of functions, especially important are power series; Fourier series; Dirichlet series, and, in general, series obtained by the expansion of functions in terms of the eigenfunctions of some operator. Many of the stated properties of series of functions can be extended to more general series with terms which are functions with values in linear normed spaces or, more generally, in linear topological spaces, and also to multiple series of functions, i.e. series whose terms are provided with multi-indices:
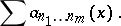 |
The theory of series of functions provides convenient and quite general methods for studying functions, since a rather wide class of functions can be represented in a certain sense as the sum of a series of elementary functions. For example, a single-valued analytic function is the sum of its Taylor series in a neighbourhood of each interior point of its domain of definition; any continuous function on some interval is the sum of a series converging uniformly on this interval with algebraic polynomials as terms; finally, for any measurable almost-everywhere finite function on the interval 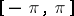 there exists a trigonometric series
there exists a trigonometric series
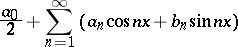 |
whose sum coincides almost-everywhere with the given function (D.E. Menshov, 1941).
The expansion of functions in series is used in different areas of mathematics: in analysis — to study functions, to look for solutions of various equations containing unknown functions in the form of series, for example, by the method of indefinite coefficients (cf. Undetermined coefficients, method of), in numerical methods for the approximate calculation of the values of functions, etc.
Historical remarks.
Already the scientists of Ancient Greece had arrived at the notion of infinite sums: the sum of the terms of an infinite geometric progression with a positive ratio less than 1 can be found in their studies. As an independent concept the notion of a series entered mathematics in the 17th century. I. Newton and G. Leibniz systematically used series to solve both algebraic and differential equations. The formal theory of series was intensively developed in the 18th century and 19th century by Jacob and Johann Bernoulli, B. Taylor, C. MacLaurin, L. Euler, J. d'Alembert, J.L. Lagrange, and others. During this period both convergent and divergent series were used, though it was not completely clear whether the operations carried out on them were legitimate. The exact theory of series was created in the 19th century on the basis of the notion of a limit by C.F. Gauss, B. Bolzano, A.L. Cauchy, P.G.L. Dirichlet, N.H. Abel, K. Weierstrass, B. Riemann, and others.
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) MR1025126 MR0708717 MR0630899 MR0435771 MR0377444 MR0234241 MR0215962 MR0118796 MR1530727 MR0118795 MR0085462 MR0070045 Zbl 0932.46001 Zbl 0672.46001 Zbl 0501.46001 Zbl 0501.46002 Zbl 0235.46001 Zbl 0103.08801 |
| [2] | N.N. Luzin, "Theory of functions of a real variable" , Moscow (1948) (In Russian) MR0036819 |
| [3] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) Zbl 0307.46024 |
| [4] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) MR0030620 Zbl 0032.05801 |
| [5] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) MR0362811 Zbl 0524.65001 |
| [6] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [7] | L.D. Kudryavtsev, "A course in mathematical analysis" , 1–3 , Moscow (1988–1989) (In Russian) MR1070567 MR1070566 MR1070565 MR0767983 MR0767982 MR0628614 MR0619214 Zbl 0703.26001 Zbl 0485.26002 Zbl 0485.26001 |
| [8] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) Zbl 0397.00003 Zbl 0384.00004 |
| [9] | V.V. Nemytskii, M.I. Sludskaya, A.N. Cherkasov, "A course of mathematical analysis" , 1–2 , Moscow-Leningrad (1944) |
Comments
Cf. also Summation methods; Summation of divergent series.
References
| [a1] | T.J. Bromwich, "An introduction to the theory of infinite series" , Macmillan (1949) MR1521495 Zbl 0901.40001 Zbl 0133.00801 Zbl 0004.00705 Zbl 52.0208.05 Zbl 39.0306.02 |
| [a2] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) MR0604364 Zbl 0454.26001 |
| [a3] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) MR0171116 Zbl 0129.28002 |
| [a4] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) MR0028430 Zbl 0124.28302 |
| [a5] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) pp. Chapt. X MR0933759 Zbl 0628.42001 |
Series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Series&oldid=30011