Schur functions in algebraic combinatorics
The Schur functions  are a special basis for the algebra of symmetric functions
are a special basis for the algebra of symmetric functions  . They are also intimately connected with representations of the symmetric and general linear groups (cf. also Representation of the symmetric groups). Standard references are [a3], [a6], [a8], [a9].
. They are also intimately connected with representations of the symmetric and general linear groups (cf. also Representation of the symmetric groups). Standard references are [a3], [a6], [a8], [a9].
Definitions.
Let  be a set of variables and let
be a set of variables and let  be the algebra of symmetric functions in
be the algebra of symmetric functions in  . Bases for this algebra are indexed by partitions
. Bases for this algebra are indexed by partitions  , i.e.,
, i.e.,  is a weakly decreasing sequence of
is a weakly decreasing sequence of  non-negative integers
non-negative integers  called parts. Associated with any partition is an alternant, which is the
called parts. Associated with any partition is an alternant, which is the  determinant
determinant
 |
In particular, for the partition  one has the Vandermonde determinant
one has the Vandermonde determinant 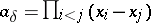 . In his thesis [a11], I. Schur defined the functions which bear his name as
. In his thesis [a11], I. Schur defined the functions which bear his name as
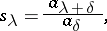 |
where addition of partitions is component-wise. It is clear from this equation that 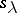 is a symmetric homogeneous polynomial of degree
is a symmetric homogeneous polynomial of degree 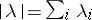 .
.
There is a more combinatorial definition of a Schur function. A partition  can be viewed as a Ferrers shape, obtained by placing dots or cells in
can be viewed as a Ferrers shape, obtained by placing dots or cells in 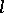 left-justified rows with
left-justified rows with  boxes in row
boxes in row 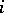 . One obtains a semi-standard Young tableaux,
. One obtains a semi-standard Young tableaux, 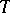 , of shape
, of shape 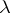 by replacing each dot by a positive integer so that rows weakly increase and columns strictly increase (cf. also Young tableau). For example, if
by replacing each dot by a positive integer so that rows weakly increase and columns strictly increase (cf. also Young tableau). For example, if 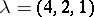 , then its shape and a possible tableau are
, then its shape and a possible tableau are
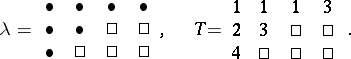 |
Each tableau determines a monomial 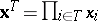 , e.g., in the example above,
, e.g., in the example above, 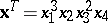 . The second definition of the Schur function is then
. The second definition of the Schur function is then
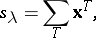 |
where the sum is over all semi-standard Young tableaux of shape 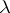 with entries between
with entries between 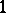 and
and 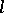 .
.
Change of basis.
The Schur functions can also be written in terms of the other standard bases for  . A monomial symmetric function
. A monomial symmetric function 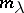 is the sum of all monomials whose exponent sequence is some permutation of
is the sum of all monomials whose exponent sequence is some permutation of 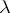 . Also, define the Kostka number [a5]
. Also, define the Kostka number [a5] 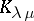 as the number of semi-standard Young tableaux
as the number of semi-standard Young tableaux 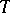 of shape
of shape 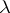 and content
and content  , i.e.,
, i.e., 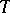 contains
contains 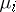 entries equal to
entries equal to 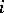 for
for  . The combinatorial definition of
. The combinatorial definition of 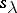 immediately gives the following rule, known as Young's rule:
immediately gives the following rule, known as Young's rule:
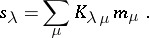 |
Now consider the complete homogeneous symmetric functions 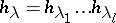 and the elementary symmetric functions
and the elementary symmetric functions  , where
, where  (respectively,
(respectively,  ) is the sum of all (respectively, all square-free) monomials of degree
) is the sum of all (respectively, all square-free) monomials of degree  . Also, let
. Also, let 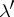 denote the partition conjugate to
denote the partition conjugate to  , whose parts are the column lengths of
, whose parts are the column lengths of 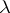 's shape. In the preceding example,
's shape. In the preceding example, 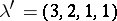 . For the two bases under consideration, the function
. For the two bases under consideration, the function  can be described as a determinant (the Jacobi–Trudi identity [a2], [a12] and its dual):
can be described as a determinant (the Jacobi–Trudi identity [a2], [a12] and its dual):
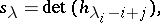 |
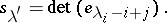 |
Note that this identity immediately implies
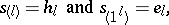 |
where  is the partition with
is the partition with  parts all equal to
parts all equal to  . These specializations also follow directly from the combinatorial definition of
. These specializations also follow directly from the combinatorial definition of 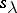 .
.
Representations.
The description of 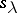 in terms of the power sum symmetric functions brings in the representation theory of the symmetric group
in terms of the power sum symmetric functions brings in the representation theory of the symmetric group 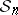 . The irreducible representations of
. The irreducible representations of 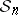 are indexed by partitions
are indexed by partitions  such that
such that 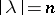 . Given a conjugacy class of
. Given a conjugacy class of  corresponding to a partition
corresponding to a partition  , let
, let  denote its size and let
denote its size and let  be the value of the
be the value of the  th irreducible character on the class. Now consider the power sum symmetric function
th irreducible character on the class. Now consider the power sum symmetric function  , where
, where 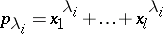 .
.
The following now holds: If 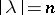 , then
, then
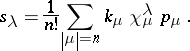 |
In other words, 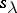 is the cycle-indicator generating function (in the sense of Polyá–Redfield enumeration) for the irreducible character of
is the cycle-indicator generating function (in the sense of Polyá–Redfield enumeration) for the irreducible character of  corresponding to
corresponding to 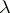 .
.
Now, consider the complex general linear group  . A representation
. A representation  is polynomial if, for every
is polynomial if, for every 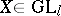 , the entries of
, the entries of 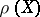 are polynomials in the entries of
are polynomials in the entries of 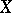 . The polynomial representations of
. The polynomial representations of  are indexed by the partitions
are indexed by the partitions  with
with 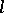 non-negative parts. Let
non-negative parts. Let 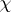 be the character of a polynomial representation
be the character of a polynomial representation 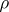 and let
and let  have eigenvalues
have eigenvalues  . Then
. Then 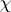 is a polynomial function of the
is a polynomial function of the  (because this is true for diagonalizable
(because this is true for diagonalizable 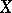 and these are dense in
and these are dense in  ) and is symmetric (because
) and is symmetric (because  is a class function). In fact, more is true: The irreducible polynomial characters of
is a class function). In fact, more is true: The irreducible polynomial characters of 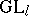 are precisely the
are precisely the  for
for  with
with  non-negative parts.
non-negative parts.
Properties.
The connection with representations of  can be used to construct an isomorphism of algebras. Let
can be used to construct an isomorphism of algebras. Let 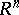 denote the vector space of all class functions on
denote the vector space of all class functions on 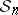 and let
and let 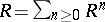 . The irreducible characters form a basis for
. The irreducible characters form a basis for 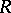 , and it can be endowed with a multiplication by induction of the tensor product. The characteristic or Frobenius mapping [a1]
, and it can be endowed with a multiplication by induction of the tensor product. The characteristic or Frobenius mapping [a1] 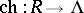 is defined on
is defined on 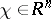 by
by
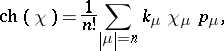 |
where 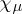 is the value of
is the value of 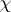 on the class corresponding to
on the class corresponding to 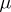 . The mapping
. The mapping 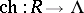 is an isomorphism of algebras. In fact, there are natural inner products on
is an isomorphism of algebras. In fact, there are natural inner products on 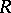 and
and 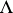 that make
that make 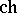 an isometry.
an isometry.
A number of identities involving Schur functions have interesting bijective proofs using the combinatorial definition. Among the most famous are the following, in which it is assumed that 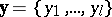 is another set of variables.
is another set of variables.
The Cauchy identity and its dual are
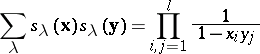 |
and
 |
D. Knuth [a4] has given algorithmic bijections between matrices and semi-standard Young tableaux that prove these identities. It is a generalization of a mapping of C. Schensted [a10] for standard Young tableaux, i.e., semi- standard Young tableaux where the entries are precisely 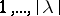 .
.
One can also describe the structure constants for the algebra  in the basis
in the basis 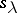 combinatorially. If
combinatorially. If 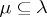 as Ferrers shapes, then one has a skew shape
as Ferrers shapes, then one has a skew shape 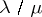 consisting of all dots or cells that are in
consisting of all dots or cells that are in 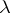 but not in
but not in 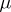 . Skew semi-standard Young tableaux are defined in the obvious way. The reverse row word for a semi-standard Young tableaux
. Skew semi-standard Young tableaux are defined in the obvious way. The reverse row word for a semi-standard Young tableaux 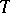 ,
, 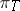 , is obtained by reading the entries in each row from right to left, starting with the top row and working down. For the example tableau,
, is obtained by reading the entries in each row from right to left, starting with the top row and working down. For the example tableau,  . Also, a sequence of positive integers
. Also, a sequence of positive integers 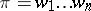 is a lattice permutation or ballot sequence if, in every prefix
is a lattice permutation or ballot sequence if, in every prefix  , the number of
, the number of 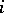 's is at least as big as the number of
's is at least as big as the number of 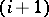 's for all
's for all 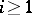 . The Littlewood–Richardson rule [a7] states that if
. The Littlewood–Richardson rule [a7] states that if
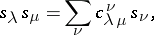 |
then 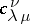 is equal to the number of semi-standard Young tableaux
is equal to the number of semi-standard Young tableaux 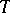 of shape
of shape  and content
and content 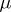 such that
such that 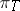 is a ballot sequence. Via the characteristic mapping, the Littlewood–Richardson coefficients
is a ballot sequence. Via the characteristic mapping, the Littlewood–Richardson coefficients 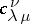 can also be viewed as giving the multiplicities of the character product
can also be viewed as giving the multiplicities of the character product  when decomposed into irreducibles. Equivalently, one can consider the decomposition of the inner tensor product of two irreducible polynomial representations of
when decomposed into irreducibles. Equivalently, one can consider the decomposition of the inner tensor product of two irreducible polynomial representations of 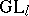 .
.
There are many generalizations of Schur functions, one of the most notable being the Hall–Littlewood functions. See [a8] for more information.
References
| [a1] | F.G. Frobenius, "Über die Charactere der symmetrischen Gruppe" Sitz. K. Preuss. Akad. Wiss (1900) pp. 516–534 (Also: Gesammelte Abh. 3 Springer, 1968, 148-166) |
| [a2] | C. Jacobi, "De functionibus alternantibus earumque divisione per productum e differentiis elementorum conflatum" J. Reine Angew. Math. , 22 (1841) pp. 360–371 (Also: Math. Werke 3, Chelsea, 1969, 439-452) |
| [a3] | G.D. James, A. Kerber, "The representation theory of the symmetric group" , Encycl. Math. Appl. , 16 , Addison-Wesley (1981) |
| [a4] | D.E. Knuth, "Permutations, matrices and generalized Young tableaux" Pacific J. Math. , 34 (1970) pp. 709–727 |
| [a5] | C. Kostka, "Über den Zusammenhang zwischen einigen Formen von symmetrischen Funktionen" Crelle's J. , 93 (1882) pp. 89–123 |
| [a6] | D.E. Littlewood, "The theory of group characters" , Oxford Univ. Press (1950) |
| [a7] | D.E. Littlewood, A.R. Richardson, "Group characters and algebra" Philos. Trans. R. Soc. London Ser. A , 233 (1934) pp. 99–142 |
| [a8] | I.G. Macdonald, "Symmetric functions and Hall polynomials" , Oxford Univ. Press (1995) (Edition: Second) |
| [a9] | B.E. Sagan, "The symmetric group: representations, combinatorial algorithms, and symmetric functions" , Wadsworth&Brooks/Cole (1991) (Second ed.: Springer, to appear) |
| [a10] | C. Schensted, "Longest increasing and decreasing subsequences" Canad. J. Math. , 13 (1961) pp. 179–191 |
| [a11] | I. Schur, "Über eine Klasse von Matrizen die sich einer gegeben Matrix zuordnen lassen" Inaugural Diss. Berlin (1901) |
| [a12] | N. Trudi, "Intorno un determinante piu generale di quello che suol dirsi determinante delle radici di una equazione, ed alle funzioni simmetriche complete di queste radici" Rend. Accad. Sci. Fis. Mat. Napoli , 3 (1864) pp. 121–134 (Also: Giornale di Mat. 2 (1864), 152–158; 180–186) |
Schur functions in algebraic combinatorics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schur_functions_in_algebraic_combinatorics&oldid=12445