S-duality
stationary duality, Spanier duality
A duality in homotopy theory which exists (in the absence of restrictions imposed on the dimensions of spaces) for the analogues of ordinary homotopy and cohomotopy groups in the suspension category — for the $ S $- homotopy and $ S $- cohomotopy groups or stationary homotopy and cohomotopy groups, forming extra-ordinary (generalized) homology and cohomology theories. A suspension category, or $ S $- category, is a category whose objects are topological spaces $ X $, while its morphisms are classes $ \{ f \} $ of $ S $- homotopic mappings $ f $ from a $ p $- fold suspension $ S ^ {p} X _ {1} $ into $ S ^ {p} X _ {2} $, $ f $ and $ g: S ^ {q} X _ {1} \rightarrow S ^ {q} X _ {2} $ being considered as $ S $- homotopic if there exists an $ r \geq \max ( p, q) $ such that the suspensions $ S ^ {r-} p f $ and $ S ^ {r-} q g $ are homotopic in the ordinary sense. The set $ \{ X _ {1} , X _ {2} \} $ of such classes, which are known as $ S $- mappings, constitutes an Abelian group with respect to the so-called track addition [1], [2], [4], [5]. The group $ \{ X _ {1} , X _ {2} \} $ is the limit of the direct spectrum of the sets $ [ S ^ {k} X _ {1} , S ^ {k} X _ {2} ] $ of ordinary homotopy classes with suspension mappings as projections; if $ k $ is sufficiently large, it is a group spectrum with homomorphisms. There exists an isomorphism $ S: \{ X _ {1} , X _ {2} \} \rightarrow \{ SX _ {1} , SX _ {2} \} $ in which the corresponding elements are represented by one and the same mapping $ S ^ {p} X _ {1} \rightarrow S ^ {p} X _ {2} $, $ p \geq 1 $. The $ n $- dual polyhedron of the polyhedron $ X $ in a sphere $ S ^ {n} $ is an arbitrary polyhedron $ D _ {n} X $ in $ S ^ {n} $ which is an $ S $- deformation retract of the complement $ S ^ {n} \setminus X $, i.e. the morphism corresponding to the imbedding $ D _ {n} X \subset S ^ {n} \setminus X $ is an $ S $- equivalence. The polyhedron $ D _ {n} X $ exists for all $ X $, and $ X $ may be considered as $ D _ {n} ^ {2} X $.
For any polyhedra $ X _ {1} , X _ {2} $ and any polyhedra $ D _ {n} X _ {1} $ and $ D _ {n} X _ {2} $ which are dual to them, there exists a unique mapping
$$ D _ {n} : \{ X _ {1} , X _ {2} \} \rightarrow \ \{ D _ {n} X _ {2} , D _ {n} X _ {1} \} $$
satisfying the following conditions:
a) It is an involutory contravariant functorial isomorphism, i.e. $ D _ {n} $ is a homomorphism such that if
$$ i : X _ {1} \subset X _ {2} \ \textrm{ and } \ i ^ \prime : D _ {n} X _ {2} \subset D _ {n} X _ {1} , $$
then
$$ D _ {n} \{ i \} = \{ i ^ \prime \} ; $$
if
$$ \{ f _ {1} \} \in \{ X _ {1} , X _ {2} \} \ \textrm{ and } \ \ \{ f _ {2} \} \in \{ X _ {2} , X _ {3} \} , $$
then
$$ D _ {n} ( \{ f _ {2} \} \cdot \{ f _ {1} \} ) = \ D _ {n} \{ f _ {1} \} \cdot D _ {n} \{ f _ {2} \} ; $$
if $ \theta $ is an element of $ \{ X _ {1} , X _ {2} \} $ or of $ \{ D _ {n} X _ {2} , D _ {n} X _ {1} \} $, then $ D _ {n} D _ {n} \theta = \theta $.
b) The following relations are valid:
$$ SD _ {n} = D _ {n+} 1 \ \textrm{ and } \ D _ {n+} 1 S = D _ {n} , $$
where $ SD _ {n} X _ {i} $ and $ D _ {n} X _ {i} $ are considered as polyhedra, $ ( n + 1 ) $- dual to polyhedra $ X _ {i} $ and, correspondingly, $ SX _ {i} $, $ i = 1, 2; $ this means that it does not depend on $ n $ and is stationary with respect to suspension.
c) It satisfies the equation
$$ D _ {a} ^ {n} \theta _ {*} = ( D _ {n} \theta ) ^ {*} D _ {a} ^ {n} , $$
where
$$ \theta _ {*} : H _ {p} ( X _ {1} ) \rightarrow H _ {p} ( X _ {2} ) $$
and
$$ ( D _ {n} \theta ) ^ {*} : H ^ {n-} p- 1 ( D _ {n} X _ {1} ) \rightarrow H ^ {n-} p- 1 ( D _ {n} X _ {2} ) $$
are homomorphisms of the above homology and cohomology groups, induced by $ S $- mappings $ \theta \in \{ X _ {1} , X _ {2} \} $ and $ D _ {n} \theta $, and
$$ D _ {a} : H _ {p} ( X _ {i} ) \rightarrow H ^ {n-} p- 1 ( D _ {n} X _ {i} ) ,\ i= 1 , 2 , $$
is an isomorphism obtained from the isomorphism of Alexander duality by replacing the set $ S ^ {n} \setminus X _ {i} $ by its $ S $- deformation retract $ D _ {n} X _ {i} $.
The construction of $ D _ {n} $ is based on the representation of a given mapping as the composition of an imbedding and an $ S $- deformation retract.
The $ S $- homotopy group $ \Sigma _ {p} ( X) $ of a space $ X $ is the group $ \{ S ^ {p} , X \} $, and the $ S $- cohomotopy group $ \Sigma ^ {p} ( X) $ of $ X $ is the group $ \{ X, S ^ {p} \} $. As in ordinary homotopy theory, one defines the homomorphisms
$$ \phi _ {p} : \Sigma _ {p} ( X) \rightarrow H _ {p} ( X) , $$
$$ \phi ^ {p} : \Sigma ^ {p} ( X) \rightarrow H ^ {p} ( X) . $$
Regarding the spheres $ S ^ {p} $ and $ S ^ {n-} p- 1 $ as $ n $- dual leads to the isomorphisms
$$ D _ {n} : \Sigma _ {p} ( X) \rightarrow \Sigma ^ {n-} p- 1 ( D _ {n} X) $$
and to the commutative diagram
$$ \begin{array}{ccc} {\Sigma _ {p} ( X) } & \rightarrow ^ { {\phi _ p} } &{H _ {p} ( X) } \\ { {size - 3 {D _ {n} } } \downarrow } &{} &{\downarrow {size - 3 {D _ {a} ^ {n} } } } \\ {\Sigma ^ {n-} p- 1 ( D _ {n} ^ {X} ) } &{ \mathop \rightarrow \limits _ { {\phi ^ {n-} p- 1 }} } &{H ^ {n-} p- 1 ( D _ {n} X) } \\ \end{array} $$
Thus, the isomorphism $ D _ {n} $ connects $ S $- homotopy and $ S $- cohomotopy groups, just as the isomorphism of Alexander duality $ D _ {a} ^ {n} $ connects the homology and cohomology groups. Any duality in the $ S $- category entails a duality of ordinary homotopy classes if the conditions imposed on the space entail the existence of a one-to-one correspondence between the set of the above classes and the set of $ S $- homotopy classes.
Examples of dual assumptions in this theory include Hurewicz's isomorphism theorem and Hopf's classification theorem. $ D _ {n} $ converts one of these theorems into the other, which means that $ S $- homotopy groups are replaced by $ S $- cohomotopy groups, homology groups by cohomology groups, the mapping $ \phi _ {p} $ by the mapping $ \phi ^ {n-} p- 1 $, the smallest dimension with a non-trivial homology group by the largest dimension with a non-trivial cohomology group, and vice versa. In ordinary homotopy theory the definition of an $ n $- cohomotopy group requires that the dimension of the space does not exceed $ 2n - 2 $( or, more generally, that the space be $ ( 2n - 1) $- coconnected, $ n > 1 $), which impairs the perfectly general nature of duality.
There are several trends of generalization of the theory: e.g. studies are made of spaces with the $ S $- homotopy type of polyhedra, the relative case, a theory with supports, etc. [3], [5], , [7]. The theory was one of the starting points in the development of stationary homotopy theory [8].
References
| [1] | E.H. Spanier, "Duality and 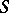 -theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 194–203 MR0085506 -theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 194–203 MR0085506 |
| [2] | E.H. Spanier, J.H.C. Whitehead, "Duality in homotopy theory" Mathematika , 2 : 3 (1955) pp. 56–80 MR0074823 Zbl 0064.17202 |
| [3] | E.H. Spanier, J.H.C. Whitehead, "Duality in relative homotopy theory" Ann. of Math. , 67 : 2 (1958) pp. 203–238 MR0105105 Zbl 0092.15701 |
| [4] | M.G. Barratt, "Track groups 1; 2" Proc. London Math. Soc. , 5 (1955) pp. 71–106; 285–329 |
| [5] | E.H. Spanier, J.H.C. Whitehead, "The theory of carriers and 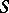 -theory" , Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 330–360 MR0084772 -theory" , Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 330–360 MR0084772 |
| [6a] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Groupes absolus" C.R. Acad. Sci. Paris , 246 : 17 (1958) pp. 2444–2447 MR0100261 Zbl 0092.39901 |
| [6b] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Suites exactes" C.R. Acad. Sci. Paris , 246 : 18 (1958) pp. 2555–2558 MR0100262 Zbl 0092.40001 |
| [6c] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Coefficients" C.R. Acad. Sci. Paris , 246 : 21 (1958) pp. 2991–2993 MR0100263 Zbl 0092.40101 |
| [6d] | B. Eckmann, P.J. Hilton, "Transgression homotopique et cohomologique" C.R. Acad. Sci. Paris , 247 : 6 (1958) pp. 620–623 MR0100264 Zbl 0092.40102 |
| [6e] | B. Eckmann, P.J. Hilton, "Décomposition homologique d'un polyhèdre simplement connexe" C.R. Acad. Sci. Paris , 248 : 14 (1959) pp. 2054–2056 |
| [7] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) MR0210112 MR1325242 Zbl 0145.43303 |
| [8] | G.W. Whitehead, "Recent advances in homotopy theory" , Amer. Math. Soc. (1970) MR0309097 Zbl 0217.48601 |
S-duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=S-duality&oldid=49574