Difference between revisions of "S-duality"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48599 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''stationary duality, Spanier duality'' | ''stationary duality, Spanier duality'' | ||
| − | A [[Duality|duality]] in homotopy theory which exists (in the absence of restrictions imposed on the dimensions of spaces) for the analogues of ordinary homotopy and cohomotopy groups in the suspension category — for the | + | A [[Duality|duality]] in homotopy theory which exists (in the absence of restrictions imposed on the dimensions of spaces) for the analogues of ordinary homotopy and cohomotopy groups in the suspension category — for the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s0830002.png" />-homotopy and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s0830003.png" />-cohomotopy groups or stationary homotopy and cohomotopy groups, forming extra-ordinary (generalized) homology and cohomology theories. A suspension category, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s0830005.png" />-category, is a [[Category|category]] whose objects are topological spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s0830006.png" />, while its morphisms are classes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s0830007.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s0830009.png" />-homotopic mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300010.png" /> from a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300011.png" />-fold [[Suspension|suspension]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300012.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300014.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300015.png" /> being considered as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300016.png" />-homotopic if there exists an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300017.png" /> such that the suspensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300019.png" /> are homotopic in the ordinary sense. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300020.png" /> of such classes, which are known as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300022.png" />-mappings, constitutes an Abelian group with respect to the so-called track addition [[#References|[1]]], [[#References|[2]]], [[#References|[4]]], [[#References|[5]]]. The group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300023.png" /> is the limit of the direct spectrum of the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300024.png" /> of ordinary homotopy classes with suspension mappings as projections; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300025.png" /> is sufficiently large, it is a group spectrum with homomorphisms. There exists an isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300026.png" /> in which the corresponding elements are represented by one and the same mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300028.png" />. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300030.png" />-dual polyhedron of the polyhedron <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300031.png" /> in a sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300032.png" /> is an arbitrary polyhedron <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300033.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300034.png" /> which is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300035.png" />-deformation retract of the complement <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300036.png" />, i.e. the morphism corresponding to the imbedding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300037.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300038.png" />-equivalence. The polyhedron <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300039.png" /> exists for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300040.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300041.png" /> may be considered as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300042.png" />. |
| − | homotopy and | ||
| − | cohomotopy groups or stationary homotopy and cohomotopy groups, forming extra-ordinary (generalized) homology and cohomology theories. A suspension category, or | ||
| − | category, is a [[Category|category]] whose objects are topological spaces | ||
| − | while its morphisms are classes | ||
| − | of | ||
| − | homotopic mappings | ||
| − | from a | ||
| − | fold [[Suspension|suspension]] | ||
| − | into | ||
| − | |||
| − | and | ||
| − | being considered as | ||
| − | homotopic if there exists an | ||
| − | such that the suspensions | ||
| − | and | ||
| − | are homotopic in the ordinary sense. The set | ||
| − | of such classes, which are known as | ||
| − | mappings, constitutes an Abelian group with respect to the so-called track addition [[#References|[1]]], [[#References|[2]]], [[#References|[4]]], [[#References|[5]]]. The group | ||
| − | is the limit of the direct spectrum of the sets | ||
| − | of ordinary homotopy classes with suspension mappings as projections; if | ||
| − | is sufficiently large, it is a group spectrum with homomorphisms. There exists an isomorphism | ||
| − | in which the corresponding elements are represented by one and the same mapping | ||
| − | |||
| − | The | ||
| − | dual polyhedron of the polyhedron | ||
| − | in a sphere | ||
| − | is an arbitrary polyhedron | ||
| − | in | ||
| − | which is an | ||
| − | deformation retract of the complement | ||
| − | i.e. the morphism corresponding to the imbedding | ||
| − | is an | ||
| − | equivalence. The polyhedron | ||
| − | exists for all | ||
| − | and | ||
| − | may be considered as | ||
| − | For any polyhedra | + | For any polyhedra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300043.png" /> and any polyhedra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300044.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300045.png" /> which are dual to them, there exists a unique mapping |
| − | and any polyhedra | ||
| − | and | ||
| − | which are dual to them, there exists a unique mapping | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300046.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
satisfying the following conditions: | satisfying the following conditions: | ||
| − | a) It is an involutory contravariant functorial isomorphism, i.e. | + | a) It is an involutory contravariant functorial isomorphism, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300047.png" /> is a homomorphism such that if |
| − | is a homomorphism such that if | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300048.png" /></td> </tr></table> | |
| − | |||
| − | |||
then | then | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300049.png" /></td> </tr></table> | |
| − | |||
| − | |||
if | if | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300050.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
then | then | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300051.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | if | + | if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300052.png" /> is an element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300053.png" /> or of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300054.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300055.png" />. |
| − | is an element of | ||
| − | or of | ||
| − | then | ||
b) The following relations are valid: | b) The following relations are valid: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300056.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300057.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300058.png" /> are considered as polyhedra, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300059.png" />-dual to polyhedra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300060.png" /> and, correspondingly, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300061.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300062.png" /> this means that it does not depend on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300063.png" /> and is stationary with respect to suspension. |
| − | and | ||
| − | are considered as polyhedra, | ||
| − | dual to polyhedra | ||
| − | and, correspondingly, | ||
| − | |||
| − | this means that it does not depend on | ||
| − | and is stationary with respect to suspension. | ||
c) It satisfies the equation | c) It satisfies the equation | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300064.png" /></td> </tr></table> | |
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300065.png" /></td> </tr></table> | |
| − | |||
| − | |||
and | and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300066.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | are homomorphisms of the above homology and cohomology groups, induced by | + | are homomorphisms of the above homology and cohomology groups, induced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300067.png" />-mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300068.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300069.png" />, and |
| − | mappings | ||
| − | and | ||
| − | and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300070.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | is an isomorphism obtained from the isomorphism of [[Alexander duality|Alexander duality]] by replacing the set | + | is an isomorphism obtained from the isomorphism of [[Alexander duality|Alexander duality]] by replacing the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300071.png" /> by its <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300072.png" />-deformation retract <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300073.png" />. |
| − | by its | ||
| − | deformation retract | ||
| − | The construction of | + | The construction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300074.png" /> is based on the representation of a given mapping as the composition of an imbedding and an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300075.png" />-deformation retract. |
| − | is based on the representation of a given mapping as the composition of an imbedding and an | ||
| − | deformation retract. | ||
| − | The | + | The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300077.png" />-homotopy group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300078.png" /> of a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300079.png" /> is the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300080.png" />, and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300082.png" />-cohomotopy group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300083.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300084.png" /> is the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300085.png" />. As in ordinary homotopy theory, one defines the homomorphisms |
| − | homotopy group | ||
| − | of a space | ||
| − | is the group | ||
| − | and the | ||
| − | cohomotopy group | ||
| − | of | ||
| − | is the group | ||
| − | As in ordinary homotopy theory, one defines the homomorphisms | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300086.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300087.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | Regarding the spheres | + | Regarding the spheres <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300088.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300089.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300090.png" />-dual leads to the isomorphisms |
| − | and | ||
| − | as | ||
| − | dual leads to the isomorphisms | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300091.png" /></td> </tr></table> | |
| − | |||
| − | |||
and to the commutative diagram | and to the commutative diagram | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300092.png" /></td> </tr></table> | |
| − | Thus, the isomorphism | + | Thus, the isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300093.png" /> connects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300094.png" />-homotopy and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300095.png" />-cohomotopy groups, just as the isomorphism of Alexander duality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300096.png" /> connects the homology and cohomology groups. Any duality in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300097.png" />-category entails a duality of ordinary homotopy classes if the conditions imposed on the space entail the existence of a one-to-one correspondence between the set of the above classes and the set of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300098.png" />-homotopy classes. |
| − | connects | ||
| − | homotopy and | ||
| − | cohomotopy groups, just as the isomorphism of Alexander duality | ||
| − | connects the homology and cohomology groups. Any duality in the | ||
| − | category entails a duality of ordinary homotopy classes if the conditions imposed on the space entail the existence of a one-to-one correspondence between the set of the above classes and the set of | ||
| − | homotopy classes. | ||
| − | Examples of dual assumptions in this theory include Hurewicz's isomorphism theorem and Hopf's classification theorem. | + | Examples of dual assumptions in this theory include Hurewicz's isomorphism theorem and Hopf's classification theorem. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s08300099.png" /> converts one of these theorems into the other, which means that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000100.png" />-homotopy groups are replaced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000101.png" />-cohomotopy groups, homology groups by cohomology groups, the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000102.png" /> by the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000103.png" />, the smallest dimension with a non-trivial homology group by the largest dimension with a non-trivial cohomology group, and vice versa. In ordinary homotopy theory the definition of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000104.png" />-cohomotopy group requires that the dimension of the space does not exceed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000105.png" /> (or, more generally, that the space be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000106.png" />-coconnected, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000107.png" />), which impairs the perfectly general nature of duality. |
| − | converts one of these theorems into the other, which means that | ||
| − | homotopy groups are replaced by | ||
| − | cohomotopy groups, homology groups by cohomology groups, the mapping | ||
| − | by the mapping | ||
| − | the smallest dimension with a non-trivial homology group by the largest dimension with a non-trivial cohomology group, and vice versa. In ordinary homotopy theory the definition of an | ||
| − | cohomotopy group requires that the dimension of the space does not exceed | ||
| − | or, more generally, that the space be | ||
| − | coconnected, | ||
| − | which impairs the perfectly general nature of duality. | ||
| − | There are several trends of generalization of the theory: e.g. studies are made of spaces with the | + | There are several trends of generalization of the theory: e.g. studies are made of spaces with the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000108.png" />-homotopy type of polyhedra, the relative case, a theory with supports, etc. [[#References|[3]]], [[#References|[5]]], , [[#References|[7]]]. The theory was one of the starting points in the development of stationary homotopy theory [[#References|[8]]]. |
| − | homotopy type of polyhedra, the relative case, a theory with supports, etc. [[#References|[3]]], [[#References|[5]]], , [[#References|[7]]]. The theory was one of the starting points in the development of stationary homotopy theory [[#References|[8]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.H. Spanier, "Duality and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000109.png" />-theory" ''Bull. Amer. Math. Soc.'' , '''62''' (1956) pp. 194–203 {{MR|0085506}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.H. Spanier, J.H.C. Whitehead, "Duality in homotopy theory" ''Mathematika'' , '''2''' : 3 (1955) pp. 56–80 {{MR|0074823}} {{ZBL|0064.17202}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.H. Spanier, J.H.C. Whitehead, "Duality in relative homotopy theory" ''Ann. of Math.'' , '''67''' : 2 (1958) pp. 203–238 {{MR|0105105}} {{ZBL|0092.15701}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.G. Barratt, "Track groups 1; 2" ''Proc. London Math. Soc.'' , '''5''' (1955) pp. 71–106; 285–329</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.H. Spanier, J.H.C. Whitehead, "The theory of carriers and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000110.png" />-theory" , ''Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz)'' , Princeton Univ. Press (1957) pp. 330–360 {{MR|0084772}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6a]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Groupes absolus" ''C.R. Acad. Sci. Paris'' , '''246''' : 17 (1958) pp. 2444–2447 {{MR|0100261}} {{ZBL|0092.39901}} </TD></TR><TR><TD valign="top">[6b]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Suites exactes" ''C.R. Acad. Sci. Paris'' , '''246''' : 18 (1958) pp. 2555–2558 {{MR|0100262}} {{ZBL|0092.40001}} </TD></TR><TR><TD valign="top">[6c]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Coefficients" ''C.R. Acad. Sci. Paris'' , '''246''' : 21 (1958) pp. 2991–2993 {{MR|0100263}} {{ZBL|0092.40101}} </TD></TR><TR><TD valign="top">[6d]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Transgression homotopique et cohomologique" ''C.R. Acad. Sci. Paris'' , '''247''' : 6 (1958) pp. 620–623 {{MR|0100264}} {{ZBL|0092.40102}} </TD></TR><TR><TD valign="top">[6e]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Décomposition homologique d'un polyhèdre simplement connexe" ''C.R. Acad. Sci. Paris'' , '''248''' : 14 (1959) pp. 2054–2056</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) {{MR|0210112}} {{MR|1325242}} {{ZBL|0145.43303}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.W. Whitehead, "Recent advances in homotopy theory" , Amer. Math. Soc. (1970) {{MR|0309097}} {{ZBL|0217.48601}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.H. Spanier, "Duality and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000109.png" />-theory" ''Bull. Amer. Math. Soc.'' , '''62''' (1956) pp. 194–203 {{MR|0085506}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.H. Spanier, J.H.C. Whitehead, "Duality in homotopy theory" ''Mathematika'' , '''2''' : 3 (1955) pp. 56–80 {{MR|0074823}} {{ZBL|0064.17202}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.H. Spanier, J.H.C. Whitehead, "Duality in relative homotopy theory" ''Ann. of Math.'' , '''67''' : 2 (1958) pp. 203–238 {{MR|0105105}} {{ZBL|0092.15701}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.G. Barratt, "Track groups 1; 2" ''Proc. London Math. Soc.'' , '''5''' (1955) pp. 71–106; 285–329</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.H. Spanier, J.H.C. Whitehead, "The theory of carriers and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000110.png" />-theory" , ''Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz)'' , Princeton Univ. Press (1957) pp. 330–360 {{MR|0084772}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6a]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Groupes absolus" ''C.R. Acad. Sci. Paris'' , '''246''' : 17 (1958) pp. 2444–2447 {{MR|0100261}} {{ZBL|0092.39901}} </TD></TR><TR><TD valign="top">[6b]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Suites exactes" ''C.R. Acad. Sci. Paris'' , '''246''' : 18 (1958) pp. 2555–2558 {{MR|0100262}} {{ZBL|0092.40001}} </TD></TR><TR><TD valign="top">[6c]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Coefficients" ''C.R. Acad. Sci. Paris'' , '''246''' : 21 (1958) pp. 2991–2993 {{MR|0100263}} {{ZBL|0092.40101}} </TD></TR><TR><TD valign="top">[6d]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Transgression homotopique et cohomologique" ''C.R. Acad. Sci. Paris'' , '''247''' : 6 (1958) pp. 620–623 {{MR|0100264}} {{ZBL|0092.40102}} </TD></TR><TR><TD valign="top">[6e]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Décomposition homologique d'un polyhèdre simplement connexe" ''C.R. Acad. Sci. Paris'' , '''248''' : 14 (1959) pp. 2054–2056</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) {{MR|0210112}} {{MR|1325242}} {{ZBL|0145.43303}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.W. Whitehead, "Recent advances in homotopy theory" , Amer. Math. Soc. (1970) {{MR|0309097}} {{ZBL|0217.48601}} </TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
stationary duality, Spanier duality
A duality in homotopy theory which exists (in the absence of restrictions imposed on the dimensions of spaces) for the analogues of ordinary homotopy and cohomotopy groups in the suspension category — for the 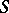 -homotopy and
-homotopy and 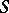 -cohomotopy groups or stationary homotopy and cohomotopy groups, forming extra-ordinary (generalized) homology and cohomology theories. A suspension category, or
-cohomotopy groups or stationary homotopy and cohomotopy groups, forming extra-ordinary (generalized) homology and cohomology theories. A suspension category, or 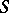 -category, is a category whose objects are topological spaces
-category, is a category whose objects are topological spaces 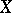 , while its morphisms are classes
, while its morphisms are classes  of
of 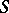 -homotopic mappings
-homotopic mappings 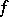 from a
from a 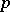 -fold suspension
-fold suspension 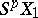 into
into 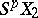 ,
, 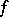 and
and 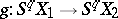 being considered as
being considered as 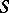 -homotopic if there exists an
-homotopic if there exists an 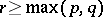 such that the suspensions
such that the suspensions 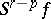 and
and  are homotopic in the ordinary sense. The set
are homotopic in the ordinary sense. The set 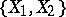 of such classes, which are known as
of such classes, which are known as 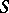 -mappings, constitutes an Abelian group with respect to the so-called track addition [1], [2], [4], [5]. The group
-mappings, constitutes an Abelian group with respect to the so-called track addition [1], [2], [4], [5]. The group 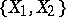 is the limit of the direct spectrum of the sets
is the limit of the direct spectrum of the sets 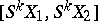 of ordinary homotopy classes with suspension mappings as projections; if
of ordinary homotopy classes with suspension mappings as projections; if 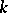 is sufficiently large, it is a group spectrum with homomorphisms. There exists an isomorphism
is sufficiently large, it is a group spectrum with homomorphisms. There exists an isomorphism 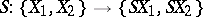 in which the corresponding elements are represented by one and the same mapping
in which the corresponding elements are represented by one and the same mapping 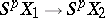 ,
, 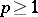 . The
. The  -dual polyhedron of the polyhedron
-dual polyhedron of the polyhedron 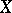 in a sphere
in a sphere 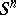 is an arbitrary polyhedron
is an arbitrary polyhedron 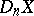 in
in 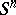 which is an
which is an 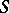 -deformation retract of the complement
-deformation retract of the complement 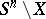 , i.e. the morphism corresponding to the imbedding
, i.e. the morphism corresponding to the imbedding 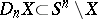 is an
is an 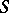 -equivalence. The polyhedron
-equivalence. The polyhedron 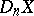 exists for all
exists for all 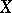 , and
, and 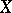 may be considered as
may be considered as 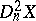 .
.
For any polyhedra 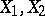 and any polyhedra
and any polyhedra 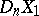 and
and 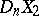 which are dual to them, there exists a unique mapping
which are dual to them, there exists a unique mapping
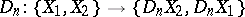 |
satisfying the following conditions:
a) It is an involutory contravariant functorial isomorphism, i.e. 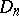 is a homomorphism such that if
is a homomorphism such that if
 |
then
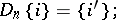 |
if
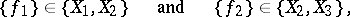 |
then
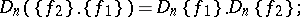 |
if 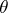 is an element of
is an element of 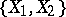 or of
or of 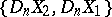 , then
, then 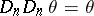 .
.
b) The following relations are valid:
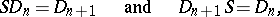 |
where 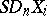 and
and 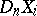 are considered as polyhedra,
are considered as polyhedra, 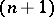 -dual to polyhedra
-dual to polyhedra 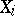 and, correspondingly,
and, correspondingly, 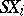 ,
, 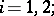 this means that it does not depend on
this means that it does not depend on  and is stationary with respect to suspension.
and is stationary with respect to suspension.
c) It satisfies the equation
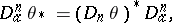 |
where
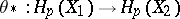 |
and
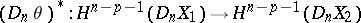 |
are homomorphisms of the above homology and cohomology groups, induced by 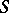 -mappings
-mappings 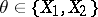 and
and 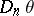 , and
, and
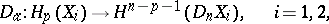 |
is an isomorphism obtained from the isomorphism of Alexander duality by replacing the set 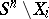 by its
by its 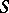 -deformation retract
-deformation retract 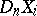 .
.
The construction of 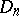 is based on the representation of a given mapping as the composition of an imbedding and an
is based on the representation of a given mapping as the composition of an imbedding and an 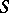 -deformation retract.
-deformation retract.
The 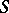 -homotopy group
-homotopy group 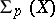 of a space
of a space 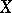 is the group
is the group 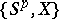 , and the
, and the 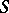 -cohomotopy group
-cohomotopy group 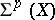 of
of 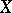 is the group
is the group 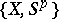 . As in ordinary homotopy theory, one defines the homomorphisms
. As in ordinary homotopy theory, one defines the homomorphisms
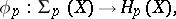 |
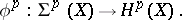 |
Regarding the spheres 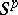 and
and 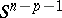 as
as  -dual leads to the isomorphisms
-dual leads to the isomorphisms
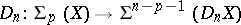 |
and to the commutative diagram
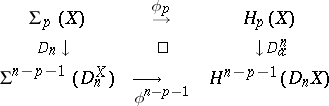 |
Thus, the isomorphism 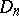 connects
connects 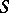 -homotopy and
-homotopy and 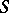 -cohomotopy groups, just as the isomorphism of Alexander duality
-cohomotopy groups, just as the isomorphism of Alexander duality 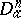 connects the homology and cohomology groups. Any duality in the
connects the homology and cohomology groups. Any duality in the 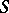 -category entails a duality of ordinary homotopy classes if the conditions imposed on the space entail the existence of a one-to-one correspondence between the set of the above classes and the set of
-category entails a duality of ordinary homotopy classes if the conditions imposed on the space entail the existence of a one-to-one correspondence between the set of the above classes and the set of 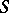 -homotopy classes.
-homotopy classes.
Examples of dual assumptions in this theory include Hurewicz's isomorphism theorem and Hopf's classification theorem. 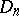 converts one of these theorems into the other, which means that
converts one of these theorems into the other, which means that 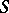 -homotopy groups are replaced by
-homotopy groups are replaced by 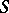 -cohomotopy groups, homology groups by cohomology groups, the mapping
-cohomotopy groups, homology groups by cohomology groups, the mapping 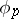 by the mapping
by the mapping 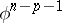 , the smallest dimension with a non-trivial homology group by the largest dimension with a non-trivial cohomology group, and vice versa. In ordinary homotopy theory the definition of an
, the smallest dimension with a non-trivial homology group by the largest dimension with a non-trivial cohomology group, and vice versa. In ordinary homotopy theory the definition of an  -cohomotopy group requires that the dimension of the space does not exceed
-cohomotopy group requires that the dimension of the space does not exceed 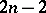 (or, more generally, that the space be
(or, more generally, that the space be 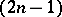 -coconnected,
-coconnected, 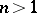 ), which impairs the perfectly general nature of duality.
), which impairs the perfectly general nature of duality.
There are several trends of generalization of the theory: e.g. studies are made of spaces with the 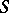 -homotopy type of polyhedra, the relative case, a theory with supports, etc. [3], [5], , [7]. The theory was one of the starting points in the development of stationary homotopy theory [8].
-homotopy type of polyhedra, the relative case, a theory with supports, etc. [3], [5], , [7]. The theory was one of the starting points in the development of stationary homotopy theory [8].
References
| [1] | E.H. Spanier, "Duality and 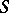 -theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 194–203 MR0085506 -theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 194–203 MR0085506 |
| [2] | E.H. Spanier, J.H.C. Whitehead, "Duality in homotopy theory" Mathematika , 2 : 3 (1955) pp. 56–80 MR0074823 Zbl 0064.17202 |
| [3] | E.H. Spanier, J.H.C. Whitehead, "Duality in relative homotopy theory" Ann. of Math. , 67 : 2 (1958) pp. 203–238 MR0105105 Zbl 0092.15701 |
| [4] | M.G. Barratt, "Track groups 1; 2" Proc. London Math. Soc. , 5 (1955) pp. 71–106; 285–329 |
| [5] | E.H. Spanier, J.H.C. Whitehead, "The theory of carriers and 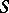 -theory" , Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 330–360 MR0084772 -theory" , Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 330–360 MR0084772 |
| [6a] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Groupes absolus" C.R. Acad. Sci. Paris , 246 : 17 (1958) pp. 2444–2447 MR0100261 Zbl 0092.39901 |
| [6b] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Suites exactes" C.R. Acad. Sci. Paris , 246 : 18 (1958) pp. 2555–2558 MR0100262 Zbl 0092.40001 |
| [6c] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Coefficients" C.R. Acad. Sci. Paris , 246 : 21 (1958) pp. 2991–2993 MR0100263 Zbl 0092.40101 |
| [6d] | B. Eckmann, P.J. Hilton, "Transgression homotopique et cohomologique" C.R. Acad. Sci. Paris , 247 : 6 (1958) pp. 620–623 MR0100264 Zbl 0092.40102 |
| [6e] | B. Eckmann, P.J. Hilton, "Décomposition homologique d'un polyhèdre simplement connexe" C.R. Acad. Sci. Paris , 248 : 14 (1959) pp. 2054–2056 |
| [7] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) MR0210112 MR1325242 Zbl 0145.43303 |
| [8] | G.W. Whitehead, "Recent advances in homotopy theory" , Amer. Math. Soc. (1970) MR0309097 Zbl 0217.48601 |
S-duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=S-duality&oldid=49415