Difference between revisions of "Root system"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) (tex done, some errors fixed) |
||
| Line 1: | Line 1: | ||
| − | A finite set | + | {{TEX|done}} |
| + | |||
| + | A finite set $ R $ | ||
| + | of vectors in a vector space $ V $ | ||
| + | over $ \mathbf R $, | ||
| + | possessing the following properties: 1) $ R $ | ||
| + | does not contain the null vector, and it generates $ V $; | ||
| + | 2) for every $ \alpha \in R $ | ||
| + | there exists an element $ \alpha ^{*} $ | ||
| + | of the space $ V ^{*} $ | ||
| + | dual to $ V $ | ||
| + | such that $ \alpha ^{*} (\alpha) =2 $ | ||
| + | and such that the endomorphism $ s _ \alpha : \ x \mapsto x-\alpha ^{*} (x) \alpha $ | ||
| + | of $ V $ | ||
| + | maps $ R $ | ||
| + | into itself; 3) $ n ( \alpha ,\ \beta ) = \beta ^{*} ( \alpha ) \in \mathbf Z $ | ||
| + | for all $ \alpha ,\ \beta \in R $. | ||
| + | |||
Sets of vectors with the properties listed above first arose in the theory of semi-simple complex Lie algebras, as weight systems of the adjoint representation of a maximal torus in such an algebra (see [[Weight of a representation of a Lie algebra|Weight of a representation of a Lie algebra]]; [[Lie algebra, semi-simple|Lie algebra, semi-simple]]). Later it was noticed that such systems of vectors appear naturally in many other branches of mathematics, such as algebraic geometry [[#References|[4]]], [[#References|[7]]], the theory of singularities [[#References|[7]]] and the theory of integer-valued quadratic forms [[#References|[5]]]. Certain problems in number theory have also turned out to be connected with root systems [[#References|[6]]]. | Sets of vectors with the properties listed above first arose in the theory of semi-simple complex Lie algebras, as weight systems of the adjoint representation of a maximal torus in such an algebra (see [[Weight of a representation of a Lie algebra|Weight of a representation of a Lie algebra]]; [[Lie algebra, semi-simple|Lie algebra, semi-simple]]). Later it was noticed that such systems of vectors appear naturally in many other branches of mathematics, such as algebraic geometry [[#References|[4]]], [[#References|[7]]], the theory of singularities [[#References|[7]]] and the theory of integer-valued quadratic forms [[#References|[5]]]. Certain problems in number theory have also turned out to be connected with root systems [[#References|[6]]]. | ||
==General properties of root systems.== | ==General properties of root systems.== | ||
| − | The endomorphism | + | The endomorphism $ s _ \alpha $ |
| + | is a [[Reflection|reflection]] relative to $ \alpha $ | ||
| + | and is uniquely determined by the properties 1) and 2). The set of fixed points of $ s _ \alpha $ | ||
| + | is $ \mathop{\rm Ker}\nolimits \ \alpha ^{*} $, | ||
| + | and $ s _ \alpha ( \alpha ) =-\alpha $. | ||
| + | The elements of $ R $ | ||
| + | are called the roots of the root system $ R $. | ||
| + | Its rank is $ \mathop{\rm dim}\nolimits \ V $. | ||
| + | A root system $ R $ | ||
| + | is said to be reduced if, for any $ \alpha \in R $, | ||
| + | the vector $ -\alpha $ | ||
| + | is the only root collinear with $ \alpha $. | ||
| + | The set $ R ^{*} = \{ {\alpha ^ *} : {\alpha \in R} \} $ | ||
| + | is a root system in $ V ^{*} $, | ||
| + | and $ \alpha ^{**} = \alpha $ | ||
| + | for all $ \alpha \in R $; | ||
| + | it is called the dual (or inverse) of $ R $. | ||
| + | The finite group $ A (R) $ | ||
| + | generated by all automorphisms of $ V $ | ||
| + | which map $ R $ | ||
| + | onto itself is called the automorphism group of the root system $ R $. | ||
| + | The subgroup $ W (R) $ | ||
| + | of $ A (R) $ | ||
| + | generated by the reflections $ s _ \alpha $, | ||
| + | $ \alpha \in R $, | ||
| + | is called the Weyl group of $ R $. | ||
| + | If $ V $ | ||
| + | is a direct sum of subspaces $ V _{i} $, | ||
| + | $ i = 1 \dots l $, | ||
| + | and $ R _{i} $ | ||
| + | is a root system in $ V _{i} $, | ||
| + | then $ R = \cup _ {i = 1} ^{l} R _{i} $ | ||
| + | is a root system in $ V $, | ||
| + | called the direct sum of the root systems $ R _{i} $. | ||
| + | A non-empty root system $ R $ | ||
| + | is said to be irreducible if it is not the direct sum of two non-empty root systems. Every root systems is the direct sum of some set of irreducible root systems, and this decomposition is unique up to the order of terms. | ||
| − | The connected components of the set | + | The connected components of the set $ V-\cup _ {\alpha \in R} \mathop{\rm Ker}\nolimits \ \alpha ^{*} $ |
| + | are open simplicial cones, known as the chambers of the root system $ R $ | ||
| + | in $ V $( | ||
| + | see [[Chamber|Chamber]]). The Weyl group acts in a simply transitive manner on the set of all chambers. The closure $ \overline{C} $ | ||
| + | of any chamber $ C $ | ||
| + | is a [[Fundamental domain|fundamental domain]] of the discrete group $ W (R) $. | ||
| + | Let $ L _{1} \dots L _{r} $ | ||
| + | be the walls of a chamber $ C $. | ||
| + | For each wall $ L _{i} $ | ||
| + | there exists a unique root $ \alpha _{i} $ | ||
| + | such that $ L _{i} = \mathop{\rm Ker}\nolimits \ \alpha _{i} ^{*} $ | ||
| + | and $ \alpha _{i} $ | ||
| + | lies on the same side of $ L _{i} $ | ||
| + | as $ C $. | ||
| + | The family of roots $ \alpha _{1} \dots \alpha _{r} $ | ||
| + | forms a basis in $ V $, | ||
| + | called the basis of the root system defined by the chamber $ C $. | ||
| + | One also says that $ \alpha _{1} \dots \alpha _{r} $ | ||
| + | is the set of simple roots defined by $ C $. | ||
| + | The group $ W (R) $ | ||
| + | is generated by the reflections $ s _ {\alpha _ i} $, | ||
| + | $ i = 1 \dots r $, | ||
| + | and moreover $ (s _ {\alpha _ i} s _ {\alpha _ j} ) ^ {m _ ij} = 1 $, | ||
| + | where $ m _{ij} $ | ||
| + | is the order of $ s _ {\alpha _ i} s _ {\alpha _ j} $, | ||
| + | is a system of defining relations for $ W (R) $, | ||
| + | so that $ W (R) $ | ||
| + | is a [[Coxeter group|Coxeter group]]. The group $ A (R) $ | ||
| + | is the semi-direct product of the subgroup of all elements in $ A (R) $ | ||
| + | that leave the set $ \alpha _{1} \dots \alpha _{r} $ | ||
| + | invariant, with $ W (R) $. | ||
| − | |||
| − | + | A choice of a chamber $ C $ | |
| + | defines an order relation on $ V $( | ||
| + | compatible with the vector-space structure), with respect to which the positive elements are precisely the linear combinations of the simple roots $ \alpha _{1} \dots \alpha _{r} $ | ||
| + | with non-negative coefficients. Any root is either positive or negative, and all its coordinates with respect to the basis $ \alpha _{1} \dots \alpha _{r} $ | ||
| + | are integers. The subgroup $ Q (R) $ | ||
| + | of $ V $ | ||
| + | generated by the root system $ R $ | ||
| + | is a lattice (i.e. a discrete subgroup of rank $ r $, | ||
| + | cf. [[Lattice in a Lie group|Lattice in a Lie group]]) invariant under the Weyl group $ W (R) $. | ||
| + | Its elements are called the radical weights of the root system $ R $. | ||
| + | The Weyl groups of root systems are precisely those discrete linear groups generated by reflections that leave no non-zero vectors fixed and possess an invariant lattice. If $ Q (R) $ | ||
| + | is regarded as a group of translations of the space $ V $, | ||
| + | then the semi-direct product $ W _{a} (R) $ | ||
| + | of $ W (R) $ | ||
| + | and $ Q (R) $ | ||
| + | is known as the affine Weyl group of $ R $. | ||
| + | $ W _{a} (R) $ | ||
| + | is a discrete group of transformations of $ V $ | ||
| + | generated by reflections in the hyperplanes $$ | ||
| + | L _ {\alpha , k} = | ||
| + | \{ {v \in V} : {\alpha ^{*} (v) = k} \} , | ||
| + | $$ | ||
| + | where $ \alpha \in R $, | ||
| + | $ k \in \mathbf Z $. | ||
| + | The quotient space of $ V $ | ||
| + | by $ W _{a} (R) $ | ||
| + | is compact; if $ R $ | ||
| + | is irreducible, then a fundamental domain for $ W _{a} (R) $ | ||
| + | is a simplex. | ||
| − | + | One can choose a positive-definite symmetric bilinear form $ ( \ ,\ ) $ | |
| + | on $ V $ | ||
| + | which is invariant under $ W (R) $( | ||
| + | the choice is not unique). This form gives $ V $ | ||
| + | the structure of a Euclidean space in which the elements of $ W (R) $ | ||
| + | are orthogonal transformations, while the reflections $ s _ \alpha $, | ||
| + | $ \alpha \in R $, | ||
| + | have the following form for all $ x \in V $: | ||
| + | $$ | ||
| + | s _ \alpha (x) = | ||
| + | x-2 (x,\ \alpha ) | ||
| − | + | \frac \alpha {( \alpha ,\ \alpha )} | |
| + | . | ||
| + | $$ | ||
| + | Using the form $ ( \ ,\ ) $, | ||
| + | one can identify the spaces $ V $ | ||
| + | and $ V ^{*} $, | ||
| + | and then $ \alpha ^{*} = 2 \alpha /( \alpha ,\ \alpha ) $; | ||
| + | condition 3) in the definition of a root system means then that $ n ( \alpha ,\ \beta ) = 2 ( \alpha ,\ \beta )/ ( \beta ,\ \beta ) \in \mathbf Z $ | ||
| + | for all $ \alpha ,\ \beta \in \mathbf R $. | ||
| − | |||
| − | + | Thanks to the form $ ( \ ,\ ) $ | |
| − | + | one can speak of metric relations between roots, in particular of the angle between roots and of the length of a root. It turns out that the magnitude of the angle is independent of the choice of $ ( \ ,\ ) $, | |
| − | + | while if a root system $ R $ | |
| + | is irreducible, then this is also true for the ratio of the lengths of two roots. | ||
==Classification of root systems.== | ==Classification of root systems.== | ||
| − | Let | + | Let $ \alpha _{1} \dots \alpha _{r} $ |
| + | be some fixed basis of a reduced root system $ R $ | ||
| + | and let $ n _{ij} = n ( \alpha _{i} ,\ \alpha _{j} ) $. | ||
| + | The matrix $ \| n _{ij} \| $, | ||
| + | $ 1 \leq i,\ j \leq r $, | ||
| + | is called the [[Cartan matrix]] of the root system $ R $; | ||
| + | this matrix has $ n _{ii} = 2 $, | ||
| + | and $ n _{ij} $( | ||
| + | $ i \neq j $) | ||
| + | may be $ 0,\ -1,\ -2 $, | ||
| + | or $ -3 $. | ||
| + | Up to permutation of indices, the Cartan matrix is independent of the choice of the basis. Two root systems with identical Cartan matrices are isomorphic. | ||
| − | With any root system one usually associates its Coxeter graph, the vertices of which are the basis elements | + | With any root system one usually associates its Coxeter graph, the vertices of which are the basis elements $ \alpha _{1} \dots \alpha _{r} $, |
| + | with vertices $ \alpha _{i} $ | ||
| + | and $ \alpha _{j} $ | ||
| + | joined by one, two or three edges or not joined at all, respectively, according as the product $ n _{ij} n _{ji} $ | ||
| + | equals $ 1,\ 2,\ 3 $, | ||
| + | or $ 0 $. | ||
| + | A root system is irreducible if and only if its Coxeter graph is connected. The Coxeter graph defines only the angles between pairs of basic roots; it does not determine the Cartan matrix (though it does determine the Weyl group): There exist dual non-isomorphic root systems with the same Coxeter graph. However, the Cartan matrix (and together with it the root system) is completely determined by the directed Coxeter graph, also known as the Dynkin diagram or simple root diagram of the root system. The direction is defined by the rule: If the simple roots $ \alpha _{i} $ | ||
| + | and $ \alpha _{j} $ | ||
| + | are not orthogonal and are different in length, the two or three edges joining the $ i $- | ||
| + | th and $ j $- | ||
| + | th vertices are assigned the inequality sign $ > $, | ||
| + | directed towards the vertex corresponding to the root of smaller length. In some cases, above each vertex of the Coxeter graph one writes a number proportional to the squared length of the corresponding root (the same proportionality factor for all the roots); this weighted graph also uniquely determines the original root system. | ||
The following is a complete list of the pairwise non-isomorphic, irreducible, reduced root systems, as defined by their simple root diagrams: vertices vertices vertices vertices | The following is a complete list of the pairwise non-isomorphic, irreducible, reduced root systems, as defined by their simple root diagrams: vertices vertices vertices vertices | ||
| Line 34: | Line 183: | ||
==Construction of the irreducible root systems.== | ==Construction of the irreducible root systems.== | ||
| − | Let | + | Let $ e _{1} \dots e _{n} $ |
| − | + | be the canonical basis in $ \mathbf R ^{n} $, | |
| − | 1 | + | $ ( \ ,\ ) $ |
| − | + | the standard scalar product in $ \mathbf R ^{n} $ | |
| − | + | for which $ (e _{i} ,\ e _{j} ) = \delta _{ij} $, | |
| + | and $ \Gamma _{n} $ | ||
| + | the lattice in $ \mathbf R ^{n} $ | ||
| + | generated by the vectors $ e _{1} \dots e _{n} $. | ||
| − | |||
| − | is a root system of type | + | 1) Let $ V $ |
| + | be a hyperplane in $ \mathbf R ^ {n + 1} $ | ||
| + | orthogonal to the vector $ e _{1} + \dots + e _ {n + 1} $. | ||
| + | Then $$ | ||
| + | R = | ||
| + | \{ {\alpha \in V \cap \Gamma _ {n + 1}} : { | ||
| + | ( \alpha ,\ \alpha ) = 2} \} = | ||
| + | $$ | ||
| + | $$ | ||
| + | = | ||
| + | \{ {e _{i} -e _ j} : {i \neq j, i,\ j = 1 \dots n + 1} \} | ||
| + | $$ | ||
| + | is a root system of type $ A _{n} $. | ||
| + | For $ n = 2 $, | ||
| + | this root system has the form | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082590b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082590b.gif" /> | ||
| Line 48: | Line 213: | ||
Figure: r082590b | Figure: r082590b | ||
| − | 2) The set of vectors | + | 2) The set of vectors $$ |
| − | + | \{ {\alpha \in \Gamma _ n} : {( \alpha ,\ \alpha ) = 1 | |
| − | + | \textrm{ or } 2} \} = | |
| − | + | $$ | |
| − | + | $$ | |
| − | + | = | |
| − | in | + | \{ {\pm e _{i} , |
| + | \pm e _{i} \pm e _ j} : {i\neq j, i,\ j = 1 \dots n} \} | ||
| + | $$ | ||
| + | in $ \mathbf R ^{n} $ | ||
| + | is a root system of type $ B _{n} $. | ||
| + | For $ n = 2 $ | ||
| + | it has the form | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082590c.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082590c.gif" /> | ||
| Line 60: | Line 231: | ||
Figure: r082590c | Figure: r082590c | ||
| − | 3) A root system of type | + | 3) A root system of type $ C _{n} $ |
| − | + | is dual to a system of type $ B _{n} $ | |
| − | + | and consists of the vectors $$ | |
| − | + | \{ {\pm e _{i} \pm e _{j} , | |
| − | 4) The set of vectors | + | \pm 2e _ i} : {i \neq j, i,\ j = 1 \dots n} \} . |
| − | + | $$ | |
| − | + | 4) The set of vectors $$ | |
| + | \{ {\alpha \in \Gamma _ n} : { | ||
| + | ( \alpha ,\ \alpha ) = 2} \} = | ||
| + | \{ {\pm e _{i} \pm e _ j} : { | ||
| + | i \neq j, i,\ j = 1 \dots n} \} | ||
| + | $$ | ||
| + | in $ \mathbf R ^{n} $ | ||
| + | is a root system of type $ D _{n} $. | ||
| − | |||
| − | 5) A root system of type | + | 5) A root system of type $ G _{2} $ |
| + | has the form | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082590d.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082590d.gif" /> | ||
| Line 76: | Line 254: | ||
Figure: r082590d | Figure: r082590d | ||
| − | and it can be described as the set of algebraic integers of the cyclotomic field generated by a cubic root of unity with norm | + | and it can be described as the set of algebraic integers of the cyclotomic field generated by a cubic root of unity with norm $ 1 $ |
| + | or $ 3 $. | ||
| − | |||
| − | + | 6) The set of vectors $$ | |
| + | \left \{ {\pm e _{i} , \pm e _{i} \pm e _{j} , | ||
| + | { | ||
| + | \frac{1}{2} | ||
| + | } ( \pm e _{1} \pm e _{2} \pm e _{3} \pm e _{4} ) | ||
| + | } : {i \neq j, i,\ j = 1 \dots 4} \right \} | ||
| + | $$ | ||
| + | in $ \mathbf R ^{4} $ | ||
| + | is a root system of type $ F _{4} $. | ||
| − | |||
| − | 7) The set of vectors | + | 7) The set of vectors $$ |
| + | \left \{ {\pm e _{i} \pm e _{j} , | ||
| + | { | ||
| + | \frac{1}{2} | ||
| + | } \sum _ {i = 1} ^ 8 | ||
| + | (-1) ^ {m (i)} e _ i} : {i \neq j, i,\ j = 1 \dots 8} | ||
| + | \textrm{ with } | ||
| + | {\sum_{i=1}^8 m (i) \equiv 0 | ||
| + | \mathop{\rm mod}\nolimits \ 2} \right \} | ||
| + | $$ | ||
| + | in $ \mathbf R ^{8} $ | ||
| + | is a root system of type $ E _{8} $. | ||
| − | |||
| − | + | 8) A root system of type $ E _{6} $ | |
| + | can be obtained as the intersection of a root system of type $ E _{8} $ | ||
| + | with the subspace of $ \mathbf R ^{8} $ | ||
| + | spanned by $ e _{1} \dots e _{6} $. | ||
| − | |||
| − | + | 9) A root system of type $ E _{7} $ | |
| + | can be obtained as the intersection of a root system of type $ E _{8} $ | ||
| + | with the subspace of $ \mathbf R ^{8} $ | ||
| + | spanned by $ e _{1} \dots e _{7} $. | ||
| − | |||
| − | + | 10) For each dimension $ n \geq 1 $ | |
| − | + | there exists (up to an isomorphism) exactly one non-reduced irreducible root system $ BC _{n} $, | |
| − | 10) For each dimension | + | namely, the union of $ B _{n} $ |
| + | and $ C _{n} $( | ||
| + | see above). For $ n = 2 $ | ||
| + | the system has the form | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082590e.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082590e.gif" /> | ||
| Line 118: | Line 320: | ||
In a sense, root systems are the combinatorial remnants of semi-simple Lie groups and one would like to express results on semi-simple Lie groups (e.g. classification of representations) in terms of the combinatorics of root systems. An example of this principle are the Kazhdan–Lusztig polynomials, defined in purely combinatorial terms of Coxeter groups, which describe the multiplicities of the composition factors for Verma modules [[#References|[a7]]]. | In a sense, root systems are the combinatorial remnants of semi-simple Lie groups and one would like to express results on semi-simple Lie groups (e.g. classification of representations) in terms of the combinatorics of root systems. An example of this principle are the Kazhdan–Lusztig polynomials, defined in purely combinatorial terms of Coxeter groups, which describe the multiplicities of the composition factors for Verma modules [[#References|[a7]]]. | ||
| − | Root systems admit a refined special function theory, partly motivated by and related to the theory of semi-simple Lie groups, such as Macdonald's identity (the affine version of the Weyl denominator formula [[#References|[6]]]), the invariant theory for | + | Root systems admit a refined special function theory, partly motivated by and related to the theory of semi-simple Lie groups, such as Macdonald's identity (the affine version of the Weyl denominator formula [[#References|[6]]]), the invariant theory for $ \theta $- |
| − | + | functions [[#References|[a8]]] and a hypergeometric-type function theory . In this latter framework also fit the constant-term conjectures of I.G. Macdonald (see below). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Most of these were first formulated and proved for $ A _{n-1} $ | |
| + | or $ BC _{n} $ | ||
| + | without any reference to root systems. Dyson's conjecture can be stated as: $$ | ||
| + | CT \prod _ {1 \leq i \neq j \leq n} | ||
| + | \left ( 1- | ||
| + | \frac{x _ i}{x _ j} | ||
| + | \right ) ^{k} = | ||
| − | + | \frac{(nk) !}{(k!) ^ n} | |
| + | , | ||
| + | $$ | ||
| + | where $ k $ | ||
| + | is a non-negative integer and $ CT $ | ||
| + | denotes the constant term coefficient in the Laurent series expansion in $ x _{1} \dots x _{n} $. | ||
| + | Macdonald's conjecture [[#References|[a5]]] generalizes this from root system $ A _{n-1} $ | ||
| + | to an arbitrary not necessarily reduced root system $ R $ | ||
| + | as follows. For each $ \alpha \in R $, | ||
| + | let $ k _ \alpha $ | ||
| + | be a non-negative integer depending only on the length of $ \alpha $. | ||
| + | Let $ R _{+} $ | ||
| + | be a choice of the set of positive roots. Put $ \rho _{k} = (1/2) \sum _ {\alpha \in R _ +} k _ \alpha \alpha $ | ||
| + | and $ k _ {\alpha /2} =0 $ | ||
| + | if $ \alpha / 2 \notin R $. | ||
| + | Then $$ | ||
| + | CT \prod _ {\alpha \in R} | ||
| + | ( 1 - e ^ \alpha ) ^ | ||
| + | {k _ \alpha} = \prod _ {\alpha \in R} | ||
| − | + | \frac{( | \alpha ^ \star ( \rho _{k} ) +k _ \alpha + ( | |
| + | 1/2)k _ {\alpha /2} |) !}{(| \alpha ^ \star ( \rho _{k} ) + (1/2)k _ {\alpha /2} |)!} | ||
| + | . | ||
| + | $$ | ||
| + | Selberg's integral is: $$ | ||
| + | \int\limits _{0} ^ 1 \dots \int\limits _{0} ^ 1 | ||
| + | {\prod _{i=1} ^ n t _{i} ^{x-1} ( 1-t _{i} ) ^{y-1} \prod _ {1 \leq i < j \leq n} | ||
| + | | t _{i} -t _{j} | ^ 2z} \ {dt _{1} \dots dt _ n} = | ||
| + | $$ | ||
| + | $$ | ||
| + | = | ||
| + | \prod _{j=0} ^ n-1 | ||
| + | \frac{\Gamma (x+jz) \Gamma (y+jz) | ||
| + | \Gamma ((j+1)z+1)}{\Gamma (x+y+(n+j-1)z) \Gamma (z+1)} | ||
| + | . | ||
| + | $$ | ||
| + | For $ x,\ y ,\ z $ | ||
| + | taking values in a discrete set, it is equivalent to Macdonald's $ BC _{n} $ | ||
| + | conjecture. Similarly, the left-hand side in Macdonald's general conjecture can be rewritten as $$ | ||
| + | \int\limits _{T} {\prod _ {\alpha \in R} (1- e ^ {i \alpha (x)} ) ^ {k _ \alpha}} \ {dx} | ||
| + | $$ | ||
| + | or $$ | ||
| + | \int\limits _{T} {\prod _ {\alpha \in R _ +} | ||
| + | | e ^ {- i \alpha (x) /2}-e ^ {i \alpha (x) /2} | ^ {2k _ \alpha} } \ {dx}, | ||
| + | $$ | ||
| + | where $ T $ | ||
| + | is the torus $ V ^ \star /(2 \pi Q(R ^ \star )) $ | ||
| + | and $ dx $ | ||
| + | is normalized Lebesgue measure on $ T $. | ||
| + | Macdonald's conjecture was proved for special root systems by various authors in various different ways. See the survey [[#References|[a1]]] for references and for a description of $ q $- | ||
| + | analogues and of Moris' conjecture related to affine root systems. Finally, Macdonald's conjecture was proved in [[#References|[a6]]] in full generality and without use of the classification of root systems. The proof used shift operators and orthogonal polynomials (Jacobi polynomials) related to the root system. | ||
| − | + | Let $ P = \{ {\lambda \in V} : {\alpha ^ \star ( \lambda ) \in \mathbf Z \textrm{ for all } \alpha \in R} \} $ | |
| + | be the weight lattice for $ R $ | ||
| + | and let $ P _{+} $ | ||
| + | consist of all weights $ \lambda $ | ||
| + | for which $ \alpha ^ \star ( \lambda ) \geq 0 $ | ||
| + | for all $ \alpha $ | ||
| + | in $ R _{+} $. | ||
| + | Let $ \geq $ | ||
| + | be the partial order on $ P $ | ||
| + | such that $ \lambda \geq \mu $ | ||
| + | if $ \lambda-\mu $ | ||
| + | is a linear combination of positive roots with non-negative integer coefficients. On the space of exponential polynomials on $ T $( | ||
| + | spanned by $ e ^ {i \lambda} $, | ||
| + | $ \lambda \in P $) | ||
| + | which are moreover invariant under the Weyl group $ W $, | ||
| + | define the Hermitian inner product $$ | ||
| + | (f,\ g) _{k} = \int\limits _{T} | ||
| + | {f(x) \overline{ {g(x)}} \prod _ {\alpha \in R _ +} | ||
| + | | e ^ {- i \alpha (x)/2}-e ^ {i \alpha (x)/2} | ^ {2k _ \alpha}} \ {dx}, | ||
| + | $$ | ||
| + | where the $ k _ \alpha $ | ||
| + | are non-negative real numbers depending only on $ | \alpha | $. | ||
| + | For $ \mu \in P _{+} $ | ||
| + | the Jacobi polynomial $ P _ \mu ^{k} $ | ||
| + | is defined on $ T $ | ||
| + | by: | ||
| − | + | 1) $ P _ \mu ^{k} (x) = \sum _ {\lambda \in C ( \mu )} \Gamma _ \lambda ( \mu ,\ k )e ^ {i \lambda (x)} $( | |
| + | here $ C( \mu ) $ | ||
| + | is the convex hull of $ W \cdot \mu $, | ||
| + | intersected with $ \mu + Q(R) $) | ||
| + | with $ \Gamma _ \mu ( \mu ,\ k ) =1 $ | ||
| + | and $ \Gamma _ {w \lambda} ( \mu ,\ k ) = \Gamma _ \lambda ( \mu ,\ k ) $, | ||
| + | $ \forall w \in W $. | ||
| − | |||
| − | + | 2) $ (P _ \mu ^{k} ,\ P _{v} ^{k} ) _{k} = 0 $ | |
| + | for all $ v \in P _{+} $ | ||
| + | with $ v < \mu $. | ||
| − | |||
| − | + | It was shown in [[#References|[a2]]], and subsequently much easier in [[#References|[a3]]], that $ (P _ \mu ^{k} ,\ P _{v} ^{k} ) _{k} =0 $ | |
| + | whenever $ \mu \neq v $. | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Habsieger, "Macdonald conjectures and the Selberg integral" , ''q-Series and Partitions'' , ''IMA Vol. Math. Appl.'' , '''18''' , Springer (1989) pp. 99–108 {{MR|1019846}} {{ZBL|0696.33002}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G.J. Heckman, "Root systems and hypergeometric functions II" ''Compositio Math.'' , '''64''' (1987) pp. 353–373 {{MR|0918416}} {{MR|0918417}} {{ZBL|0656.17007}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.J. Heckman, "An elementary approch to the hypergeometric shift operators of Opdam" ''Invent. Math.'' , '''103''' (1991) pp. 341–350</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1980) {{MR|0499562}} {{MR|0323842}} {{ZBL|0447.17002}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> I.G. Macdonald, "Some conjectures for root systems" ''SIAM J. Math. Anal.'' , '''13''' (1982) pp. 988–1007 {{MR|0674768}} {{MR|0674769}} {{ZBL|0498.17006}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> E.M. Opdam, "Some applications of hypergeometric shift operators" ''Invent. Math.'' , '''98''' (1989) pp. 1–18 {{MR|1010152}} {{ZBL|0696.33006}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> D. Kahzdan, G. Lusztig, "Representations of Coxeter groups and Hecke algebras" ''Invent. Math.'' , '''53''' (1979) pp. 165–184 {{MR|560412}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> E. Looyenga, "Root systems and elliptic curves" ''Invent. Math.'' , '''38''' (1976) pp. 17–32</TD></TR><TR><TD valign="top">[a9a]</TD> <TD valign="top"> G.J. Heckman, E.M. Opdam, "Root systems and hypergeometric functions, I, II" ''Comp. Math.'' , '''64''' (1987) pp. 329–352; 353–373 {{MR|918416}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a9b]</TD> <TD valign="top"> G.J. Heckman, E.M. Opdam, "Root systems and hypergeometric functions, III, IV" ''Comp. Math.'' , '''67''' (1988) pp. 21–49; 191–209</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> H. Freudenthal, H. de Vries, "Linear Lie groups" , Acad. Press (1969) {{MR|0260926}} {{ZBL|0377.22001}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) {{MR|0148716}} {{MR|0143793}} {{ZBL|0121.27504}} {{ZBL|0109.26201}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Habsieger, "Macdonald conjectures and the Selberg integral" , ''q-Series and Partitions'' , ''IMA Vol. Math. Appl.'' , '''18''' , Springer (1989) pp. 99–108 {{MR|1019846}} {{ZBL|0696.33002}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G.J. Heckman, "Root systems and hypergeometric functions II" ''Compositio Math.'' , '''64''' (1987) pp. 353–373 {{MR|0918416}} {{MR|0918417}} {{ZBL|0656.17007}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.J. Heckman, "An elementary approch to the hypergeometric shift operators of Opdam" ''Invent. Math.'' , '''103''' (1991) pp. 341–350</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1980) {{MR|0499562}} {{MR|0323842}} {{ZBL|0447.17002}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> I.G. Macdonald, "Some conjectures for root systems" ''SIAM J. Math. Anal.'' , '''13''' (1982) pp. 988–1007 {{MR|0674768}} {{MR|0674769}} {{ZBL|0498.17006}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> E.M. Opdam, "Some applications of hypergeometric shift operators" ''Invent. Math.'' , '''98''' (1989) pp. 1–18 {{MR|1010152}} {{ZBL|0696.33006}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> D. Kahzdan, G. Lusztig, "Representations of Coxeter groups and Hecke algebras" ''Invent. Math.'' , '''53''' (1979) pp. 165–184 {{MR|560412}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> E. Looyenga, "Root systems and elliptic curves" ''Invent. Math.'' , '''38''' (1976) pp. 17–32</TD></TR><TR><TD valign="top">[a9a]</TD> <TD valign="top"> G.J. Heckman, E.M. Opdam, "Root systems and hypergeometric functions, I, II" ''Comp. Math.'' , '''64''' (1987) pp. 329–352; 353–373 {{MR|918416}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a9b]</TD> <TD valign="top"> G.J. Heckman, E.M. Opdam, "Root systems and hypergeometric functions, III, IV" ''Comp. Math.'' , '''67''' (1988) pp. 21–49; 191–209</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> H. Freudenthal, H. de Vries, "Linear Lie groups" , Acad. Press (1969) {{MR|0260926}} {{ZBL|0377.22001}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) {{MR|0148716}} {{MR|0143793}} {{ZBL|0121.27504}} {{ZBL|0109.26201}} </TD></TR></table> | ||
Latest revision as of 19:14, 21 December 2019
A finite set $ R $
of vectors in a vector space $ V $
over $ \mathbf R $,
possessing the following properties: 1) $ R $
does not contain the null vector, and it generates $ V $;
2) for every $ \alpha \in R $
there exists an element $ \alpha ^{*} $
of the space $ V ^{*} $
dual to $ V $
such that $ \alpha ^{*} (\alpha) =2 $
and such that the endomorphism $ s _ \alpha : \ x \mapsto x-\alpha ^{*} (x) \alpha $
of $ V $
maps $ R $
into itself; 3) $ n ( \alpha ,\ \beta ) = \beta ^{*} ( \alpha ) \in \mathbf Z $
for all $ \alpha ,\ \beta \in R $.
Sets of vectors with the properties listed above first arose in the theory of semi-simple complex Lie algebras, as weight systems of the adjoint representation of a maximal torus in such an algebra (see Weight of a representation of a Lie algebra; Lie algebra, semi-simple). Later it was noticed that such systems of vectors appear naturally in many other branches of mathematics, such as algebraic geometry [4], [7], the theory of singularities [7] and the theory of integer-valued quadratic forms [5]. Certain problems in number theory have also turned out to be connected with root systems [6].
General properties of root systems.
The endomorphism $ s _ \alpha $ is a reflection relative to $ \alpha $ and is uniquely determined by the properties 1) and 2). The set of fixed points of $ s _ \alpha $ is $ \mathop{\rm Ker}\nolimits \ \alpha ^{*} $, and $ s _ \alpha ( \alpha ) =-\alpha $. The elements of $ R $ are called the roots of the root system $ R $. Its rank is $ \mathop{\rm dim}\nolimits \ V $. A root system $ R $ is said to be reduced if, for any $ \alpha \in R $, the vector $ -\alpha $ is the only root collinear with $ \alpha $. The set $ R ^{*} = \{ {\alpha ^ *} : {\alpha \in R} \} $ is a root system in $ V ^{*} $, and $ \alpha ^{**} = \alpha $ for all $ \alpha \in R $; it is called the dual (or inverse) of $ R $. The finite group $ A (R) $ generated by all automorphisms of $ V $ which map $ R $ onto itself is called the automorphism group of the root system $ R $. The subgroup $ W (R) $ of $ A (R) $ generated by the reflections $ s _ \alpha $, $ \alpha \in R $, is called the Weyl group of $ R $. If $ V $ is a direct sum of subspaces $ V _{i} $, $ i = 1 \dots l $, and $ R _{i} $ is a root system in $ V _{i} $, then $ R = \cup _ {i = 1} ^{l} R _{i} $ is a root system in $ V $, called the direct sum of the root systems $ R _{i} $. A non-empty root system $ R $ is said to be irreducible if it is not the direct sum of two non-empty root systems. Every root systems is the direct sum of some set of irreducible root systems, and this decomposition is unique up to the order of terms.
The connected components of the set $ V-\cup _ {\alpha \in R} \mathop{\rm Ker}\nolimits \ \alpha ^{*} $ are open simplicial cones, known as the chambers of the root system $ R $ in $ V $( see Chamber). The Weyl group acts in a simply transitive manner on the set of all chambers. The closure $ \overline{C} $ of any chamber $ C $ is a fundamental domain of the discrete group $ W (R) $. Let $ L _{1} \dots L _{r} $ be the walls of a chamber $ C $. For each wall $ L _{i} $ there exists a unique root $ \alpha _{i} $ such that $ L _{i} = \mathop{\rm Ker}\nolimits \ \alpha _{i} ^{*} $ and $ \alpha _{i} $ lies on the same side of $ L _{i} $ as $ C $. The family of roots $ \alpha _{1} \dots \alpha _{r} $ forms a basis in $ V $, called the basis of the root system defined by the chamber $ C $. One also says that $ \alpha _{1} \dots \alpha _{r} $ is the set of simple roots defined by $ C $. The group $ W (R) $ is generated by the reflections $ s _ {\alpha _ i} $, $ i = 1 \dots r $, and moreover $ (s _ {\alpha _ i} s _ {\alpha _ j} ) ^ {m _ ij} = 1 $, where $ m _{ij} $ is the order of $ s _ {\alpha _ i} s _ {\alpha _ j} $, is a system of defining relations for $ W (R) $, so that $ W (R) $ is a Coxeter group. The group $ A (R) $ is the semi-direct product of the subgroup of all elements in $ A (R) $ that leave the set $ \alpha _{1} \dots \alpha _{r} $ invariant, with $ W (R) $.
A choice of a chamber $ C $
defines an order relation on $ V $(
compatible with the vector-space structure), with respect to which the positive elements are precisely the linear combinations of the simple roots $ \alpha _{1} \dots \alpha _{r} $
with non-negative coefficients. Any root is either positive or negative, and all its coordinates with respect to the basis $ \alpha _{1} \dots \alpha _{r} $
are integers. The subgroup $ Q (R) $
of $ V $
generated by the root system $ R $
is a lattice (i.e. a discrete subgroup of rank $ r $,
cf. Lattice in a Lie group) invariant under the Weyl group $ W (R) $.
Its elements are called the radical weights of the root system $ R $.
The Weyl groups of root systems are precisely those discrete linear groups generated by reflections that leave no non-zero vectors fixed and possess an invariant lattice. If $ Q (R) $
is regarded as a group of translations of the space $ V $,
then the semi-direct product $ W _{a} (R) $
of $ W (R) $
and $ Q (R) $
is known as the affine Weyl group of $ R $.
$ W _{a} (R) $
is a discrete group of transformations of $ V $
generated by reflections in the hyperplanes $$
L _ {\alpha , k} =
\{ {v \in V} : {\alpha ^{*} (v) = k} \} ,
$$
where $ \alpha \in R $,
$ k \in \mathbf Z $.
The quotient space of $ V $
by $ W _{a} (R) $
is compact; if $ R $
is irreducible, then a fundamental domain for $ W _{a} (R) $
is a simplex.
One can choose a positive-definite symmetric bilinear form $ ( \ ,\ ) $ on $ V $ which is invariant under $ W (R) $( the choice is not unique). This form gives $ V $ the structure of a Euclidean space in which the elements of $ W (R) $ are orthogonal transformations, while the reflections $ s _ \alpha $, $ \alpha \in R $, have the following form for all $ x \in V $: $$ s _ \alpha (x) = x-2 (x,\ \alpha ) \frac \alpha {( \alpha ,\ \alpha )} . $$ Using the form $ ( \ ,\ ) $, one can identify the spaces $ V $ and $ V ^{*} $, and then $ \alpha ^{*} = 2 \alpha /( \alpha ,\ \alpha ) $; condition 3) in the definition of a root system means then that $ n ( \alpha ,\ \beta ) = 2 ( \alpha ,\ \beta )/ ( \beta ,\ \beta ) \in \mathbf Z $ for all $ \alpha ,\ \beta \in \mathbf R $.
Thanks to the form $ ( \ ,\ ) $
one can speak of metric relations between roots, in particular of the angle between roots and of the length of a root. It turns out that the magnitude of the angle is independent of the choice of $ ( \ ,\ ) $,
while if a root system $ R $
is irreducible, then this is also true for the ratio of the lengths of two roots.
Classification of root systems.
Let $ \alpha _{1} \dots \alpha _{r} $ be some fixed basis of a reduced root system $ R $ and let $ n _{ij} = n ( \alpha _{i} ,\ \alpha _{j} ) $. The matrix $ \| n _{ij} \| $, $ 1 \leq i,\ j \leq r $, is called the Cartan matrix of the root system $ R $; this matrix has $ n _{ii} = 2 $, and $ n _{ij} $( $ i \neq j $) may be $ 0,\ -1,\ -2 $, or $ -3 $. Up to permutation of indices, the Cartan matrix is independent of the choice of the basis. Two root systems with identical Cartan matrices are isomorphic.
With any root system one usually associates its Coxeter graph, the vertices of which are the basis elements $ \alpha _{1} \dots \alpha _{r} $, with vertices $ \alpha _{i} $ and $ \alpha _{j} $ joined by one, two or three edges or not joined at all, respectively, according as the product $ n _{ij} n _{ji} $ equals $ 1,\ 2,\ 3 $, or $ 0 $. A root system is irreducible if and only if its Coxeter graph is connected. The Coxeter graph defines only the angles between pairs of basic roots; it does not determine the Cartan matrix (though it does determine the Weyl group): There exist dual non-isomorphic root systems with the same Coxeter graph. However, the Cartan matrix (and together with it the root system) is completely determined by the directed Coxeter graph, also known as the Dynkin diagram or simple root diagram of the root system. The direction is defined by the rule: If the simple roots $ \alpha _{i} $ and $ \alpha _{j} $ are not orthogonal and are different in length, the two or three edges joining the $ i $- th and $ j $- th vertices are assigned the inequality sign $ > $, directed towards the vertex corresponding to the root of smaller length. In some cases, above each vertex of the Coxeter graph one writes a number proportional to the squared length of the corresponding root (the same proportionality factor for all the roots); this weighted graph also uniquely determines the original root system.
The following is a complete list of the pairwise non-isomorphic, irreducible, reduced root systems, as defined by their simple root diagrams: vertices vertices vertices vertices
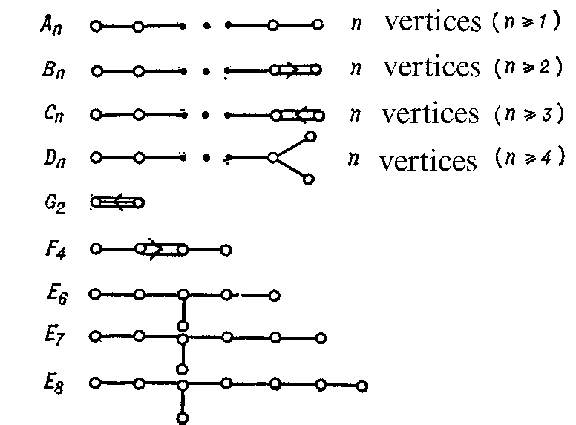
Figure: r082590a
Construction of the irreducible root systems.
Let $ e _{1} \dots e _{n} $ be the canonical basis in $ \mathbf R ^{n} $, $ ( \ ,\ ) $ the standard scalar product in $ \mathbf R ^{n} $ for which $ (e _{i} ,\ e _{j} ) = \delta _{ij} $, and $ \Gamma _{n} $ the lattice in $ \mathbf R ^{n} $ generated by the vectors $ e _{1} \dots e _{n} $.
1) Let $ V $
be a hyperplane in $ \mathbf R ^ {n + 1} $
orthogonal to the vector $ e _{1} + \dots + e _ {n + 1} $.
Then $$
R =
\{ {\alpha \in V \cap \Gamma _ {n + 1}} : {
( \alpha ,\ \alpha ) = 2} \} =
$$
$$
=
\{ {e _{i} -e _ j} : {i \neq j, i,\ j = 1 \dots n + 1} \}
$$
is a root system of type $ A _{n} $.
For $ n = 2 $,
this root system has the form
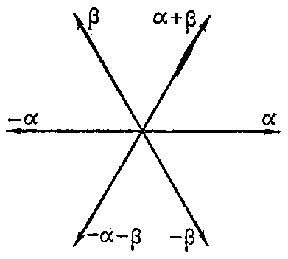
Figure: r082590b
2) The set of vectors $$ \{ {\alpha \in \Gamma _ n} : {( \alpha ,\ \alpha ) = 1 \textrm{ or } 2} \} = $$ $$ = \{ {\pm e _{i} , \pm e _{i} \pm e _ j} : {i\neq j, i,\ j = 1 \dots n} \} $$ in $ \mathbf R ^{n} $ is a root system of type $ B _{n} $. For $ n = 2 $ it has the form
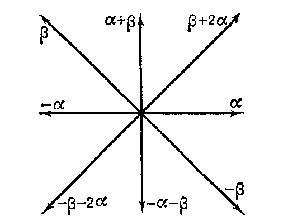
Figure: r082590c
3) A root system of type $ C _{n} $ is dual to a system of type $ B _{n} $ and consists of the vectors $$ \{ {\pm e _{i} \pm e _{j} , \pm 2e _ i} : {i \neq j, i,\ j = 1 \dots n} \} . $$ 4) The set of vectors $$ \{ {\alpha \in \Gamma _ n} : { ( \alpha ,\ \alpha ) = 2} \} = \{ {\pm e _{i} \pm e _ j} : { i \neq j, i,\ j = 1 \dots n} \} $$ in $ \mathbf R ^{n} $ is a root system of type $ D _{n} $.
5) A root system of type $ G _{2} $
has the form
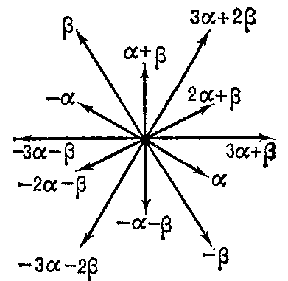
Figure: r082590d
and it can be described as the set of algebraic integers of the cyclotomic field generated by a cubic root of unity with norm $ 1 $ or $ 3 $.
6) The set of vectors $$
\left \{ {\pm e _{i} , \pm e _{i} \pm e _{j} ,
{
\frac{1}{2}
} ( \pm e _{1} \pm e _{2} \pm e _{3} \pm e _{4} )
} : {i \neq j, i,\ j = 1 \dots 4} \right \}
$$
in $ \mathbf R ^{4} $
is a root system of type $ F _{4} $.
7) The set of vectors $$
\left \{ {\pm e _{i} \pm e _{j} ,
{
\frac{1}{2}
} \sum _ {i = 1} ^ 8
(-1) ^ {m (i)} e _ i} : {i \neq j, i,\ j = 1 \dots 8}
\textrm{ with }
{\sum_{i=1}^8 m (i) \equiv 0
\mathop{\rm mod}\nolimits \ 2} \right \}
$$
in $ \mathbf R ^{8} $
is a root system of type $ E _{8} $.
8) A root system of type $ E _{6} $
can be obtained as the intersection of a root system of type $ E _{8} $
with the subspace of $ \mathbf R ^{8} $
spanned by $ e _{1} \dots e _{6} $.
9) A root system of type $ E _{7} $
can be obtained as the intersection of a root system of type $ E _{8} $
with the subspace of $ \mathbf R ^{8} $
spanned by $ e _{1} \dots e _{7} $.
10) For each dimension $ n \geq 1 $
there exists (up to an isomorphism) exactly one non-reduced irreducible root system $ BC _{n} $,
namely, the union of $ B _{n} $
and $ C _{n} $(
see above). For $ n = 2 $
the system has the form
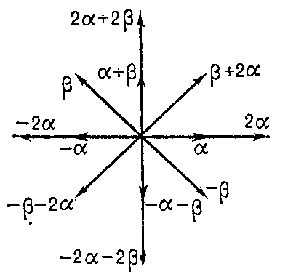
Figure: r082590e
Concerning affine root systems, see [6].
References
| [1] | N. Bourbaki, "Groupes et algèbres de Lie" , Eléments de mathématiques , Hermann (1968) pp. Chapts. 4–6 MR0240238 Zbl 0186.33001 |
| [2] | J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966) MR0215886 Zbl 0144.02105 |
| [3] | R.G. Steinberg, "Lectures on Chevalley groups" , Yale Univ. Press (1967) MR0476871 MR0466335 Zbl 0307.22001 Zbl 1196.22001 |
| [4] | Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1974) (Translated from Russian) MR0460349 Zbl 0277.14014 |
| [5] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) MR0506372 Zbl 0292.10016 |
| [6] | I.G. Macdonald, "Affine root systems and Dedekind's eta function" Invent. Math. , 15 (1972) pp. 91–143 MR357528 |
| [7] | V.I. Arnol'd, "Critical points of smooth functions and their normal forms" Russian Math. Surveys , 30 : 5 (1975) pp. 1–75 Uspekhi Mat. Nauk , 30 : 5 (1975) pp. 3–65 Zbl 0343.58001 |
Comments
In the Western literature one usually says Dynkin graph instead of Coxeter graph, especially in connection with Lie theory. The directed Coxeter graph or simple root diagram is commonly called Dynkin diagram.
See also [a4] for an introduction to root systems. Note that the notion of Coxeter graph used in the article above differs slightly from the notion used by N. Bourbaki [1].
In a sense, root systems are the combinatorial remnants of semi-simple Lie groups and one would like to express results on semi-simple Lie groups (e.g. classification of representations) in terms of the combinatorics of root systems. An example of this principle are the Kazhdan–Lusztig polynomials, defined in purely combinatorial terms of Coxeter groups, which describe the multiplicities of the composition factors for Verma modules [a7].
Root systems admit a refined special function theory, partly motivated by and related to the theory of semi-simple Lie groups, such as Macdonald's identity (the affine version of the Weyl denominator formula [6]), the invariant theory for $ \theta $- functions [a8] and a hypergeometric-type function theory . In this latter framework also fit the constant-term conjectures of I.G. Macdonald (see below).
Most of these were first formulated and proved for $ A _{n-1} $ or $ BC _{n} $ without any reference to root systems. Dyson's conjecture can be stated as: $$ CT \prod _ {1 \leq i \neq j \leq n} \left ( 1- \frac{x _ i}{x _ j} \right ) ^{k} = \frac{(nk) !}{(k!) ^ n} , $$ where $ k $ is a non-negative integer and $ CT $ denotes the constant term coefficient in the Laurent series expansion in $ x _{1} \dots x _{n} $. Macdonald's conjecture [a5] generalizes this from root system $ A _{n-1} $ to an arbitrary not necessarily reduced root system $ R $ as follows. For each $ \alpha \in R $, let $ k _ \alpha $ be a non-negative integer depending only on the length of $ \alpha $. Let $ R _{+} $ be a choice of the set of positive roots. Put $ \rho _{k} = (1/2) \sum _ {\alpha \in R _ +} k _ \alpha \alpha $ and $ k _ {\alpha /2} =0 $ if $ \alpha / 2 \notin R $. Then $$ CT \prod _ {\alpha \in R} ( 1 - e ^ \alpha ) ^ {k _ \alpha} = \prod _ {\alpha \in R} \frac{( | \alpha ^ \star ( \rho _{k} ) +k _ \alpha + ( 1/2)k _ {\alpha /2} |) !}{(| \alpha ^ \star ( \rho _{k} ) + (1/2)k _ {\alpha /2} |)!} . $$ Selberg's integral is: $$ \int\limits _{0} ^ 1 \dots \int\limits _{0} ^ 1 {\prod _{i=1} ^ n t _{i} ^{x-1} ( 1-t _{i} ) ^{y-1} \prod _ {1 \leq i < j \leq n} | t _{i} -t _{j} | ^ 2z} \ {dt _{1} \dots dt _ n} = $$ $$ = \prod _{j=0} ^ n-1 \frac{\Gamma (x+jz) \Gamma (y+jz) \Gamma ((j+1)z+1)}{\Gamma (x+y+(n+j-1)z) \Gamma (z+1)} . $$ For $ x,\ y ,\ z $ taking values in a discrete set, it is equivalent to Macdonald's $ BC _{n} $ conjecture. Similarly, the left-hand side in Macdonald's general conjecture can be rewritten as $$ \int\limits _{T} {\prod _ {\alpha \in R} (1- e ^ {i \alpha (x)} ) ^ {k _ \alpha}} \ {dx} $$ or $$ \int\limits _{T} {\prod _ {\alpha \in R _ +} | e ^ {- i \alpha (x) /2}-e ^ {i \alpha (x) /2} | ^ {2k _ \alpha} } \ {dx}, $$ where $ T $ is the torus $ V ^ \star /(2 \pi Q(R ^ \star )) $ and $ dx $ is normalized Lebesgue measure on $ T $. Macdonald's conjecture was proved for special root systems by various authors in various different ways. See the survey [a1] for references and for a description of $ q $- analogues and of Moris' conjecture related to affine root systems. Finally, Macdonald's conjecture was proved in [a6] in full generality and without use of the classification of root systems. The proof used shift operators and orthogonal polynomials (Jacobi polynomials) related to the root system.
Let $ P = \{ {\lambda \in V} : {\alpha ^ \star ( \lambda ) \in \mathbf Z \textrm{ for all } \alpha \in R} \} $ be the weight lattice for $ R $ and let $ P _{+} $ consist of all weights $ \lambda $ for which $ \alpha ^ \star ( \lambda ) \geq 0 $ for all $ \alpha $ in $ R _{+} $. Let $ \geq $ be the partial order on $ P $ such that $ \lambda \geq \mu $ if $ \lambda-\mu $ is a linear combination of positive roots with non-negative integer coefficients. On the space of exponential polynomials on $ T $( spanned by $ e ^ {i \lambda} $, $ \lambda \in P $) which are moreover invariant under the Weyl group $ W $, define the Hermitian inner product $$ (f,\ g) _{k} = \int\limits _{T} {f(x) \overline{ {g(x)}} \prod _ {\alpha \in R _ +} | e ^ {- i \alpha (x)/2}-e ^ {i \alpha (x)/2} | ^ {2k _ \alpha}} \ {dx}, $$ where the $ k _ \alpha $ are non-negative real numbers depending only on $ | \alpha | $. For $ \mu \in P _{+} $ the Jacobi polynomial $ P _ \mu ^{k} $ is defined on $ T $ by:
1) $ P _ \mu ^{k} (x) = \sum _ {\lambda \in C ( \mu )} \Gamma _ \lambda ( \mu ,\ k )e ^ {i \lambda (x)} $( here $ C( \mu ) $ is the convex hull of $ W \cdot \mu $, intersected with $ \mu + Q(R) $) with $ \Gamma _ \mu ( \mu ,\ k ) =1 $ and $ \Gamma _ {w \lambda} ( \mu ,\ k ) = \Gamma _ \lambda ( \mu ,\ k ) $, $ \forall w \in W $.
2) $ (P _ \mu ^{k} ,\ P _{v} ^{k} ) _{k} = 0 $
for all $ v \in P _{+} $
with $ v < \mu $.
It was shown in [a2], and subsequently much easier in [a3], that $ (P _ \mu ^{k} ,\ P _{v} ^{k} ) _{k} =0 $
whenever $ \mu \neq v $.
References
| [a1] | L. Habsieger, "Macdonald conjectures and the Selberg integral" , q-Series and Partitions , IMA Vol. Math. Appl. , 18 , Springer (1989) pp. 99–108 MR1019846 Zbl 0696.33002 |
| [a2] | G.J. Heckman, "Root systems and hypergeometric functions II" Compositio Math. , 64 (1987) pp. 353–373 MR0918416 MR0918417 Zbl 0656.17007 |
| [a3] | G.J. Heckman, "An elementary approch to the hypergeometric shift operators of Opdam" Invent. Math. , 103 (1991) pp. 341–350 |
| [a4] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1980) MR0499562 MR0323842 Zbl 0447.17002 |
| [a5] | I.G. Macdonald, "Some conjectures for root systems" SIAM J. Math. Anal. , 13 (1982) pp. 988–1007 MR0674768 MR0674769 Zbl 0498.17006 |
| [a6] | E.M. Opdam, "Some applications of hypergeometric shift operators" Invent. Math. , 98 (1989) pp. 1–18 MR1010152 Zbl 0696.33006 |
| [a7] | D. Kahzdan, G. Lusztig, "Representations of Coxeter groups and Hecke algebras" Invent. Math. , 53 (1979) pp. 165–184 MR560412 |
| [a8] | E. Looyenga, "Root systems and elliptic curves" Invent. Math. , 38 (1976) pp. 17–32 |
| [a9a] | G.J. Heckman, E.M. Opdam, "Root systems and hypergeometric functions, I, II" Comp. Math. , 64 (1987) pp. 329–352; 353–373 MR918416 |
| [a9b] | G.J. Heckman, E.M. Opdam, "Root systems and hypergeometric functions, III, IV" Comp. Math. , 67 (1988) pp. 21–49; 191–209 |
| [a10] | H. Freudenthal, H. de Vries, "Linear Lie groups" , Acad. Press (1969) MR0260926 Zbl 0377.22001 |
| [a11] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) MR0148716 MR0143793 Zbl 0121.27504 Zbl 0109.26201 |
Root system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Root_system&oldid=44314