Ro-group

right-ordered group

A group endowed with a total order such that for all ,

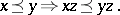If is the positive cone of the -group (cf. also -group), then:

1) ;

2) ;

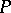3) . If, in a group , there is a subset satisfying 1)–3), then 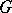can given the structure of a -group with positive cone 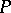by a setting 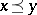if and only if . The positive cone of a -group is isolated, i.e., .

The group of order automorphisms of a totally ordered set can be turned into a -group by defining the following relation on it. Let be any well ordering on : . Let 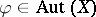and let be the first (with respect to ) element in 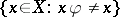. Then 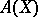is a -group with respect to the order with positive cone

Any 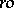-group is isomorphic to a subgroup of the -group for some totally ordered set . There exist simple -groups whose finitely generated subgroups coincide with the commutator subgroup. The class of all groups that can be turned into a -group is a quasi-variety, i.e., it is defined by a system of formulas of the form:

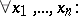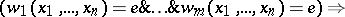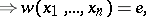where , are the group-theoretical words. This class is closed under formation of subgroups, Cartesian and free products, and extension, and is locally closed.

The system of convex subgroups of a -group is a complete chain. It can be non-solvable, non-infra-invariant and non-normal. There exist non-Abelian -groups without proper convex subgroups.

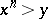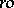A -group is Archimedean if for any positive elements there exists a positive integer such that . An Archimedean -group is order-isomorphic to some subgroup of the additive group of real numbers with the natural order. The class of Conradian -groups, i.e., -groups for which the system is subnormal and the quotient groups of the jumps of are Archimedean, is well investigated.

References

[a1]	V.M. Kopytov, N.Ya. Medvedev, "The theory of lattice-ordered groups" , Kluwer Acad. Publ. (1994) (In Russian)
[a2]	R.T.B. Mura, A.H. Rhemtulla, "Orderable groups" , M. Dekker (1977)