Ringed space
A topological space 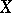 with a sheaf of rings
with a sheaf of rings 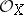 . The sheaf
. The sheaf 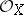 is called the structure sheaf of the ringed space
is called the structure sheaf of the ringed space 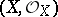 . It is usually understood that
. It is usually understood that 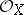 is a sheaf of associative and commutative rings with a unit element. A pair
is a sheaf of associative and commutative rings with a unit element. A pair 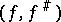 is called a morphism from a ringed space
is called a morphism from a ringed space 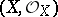 into a ringed space
into a ringed space 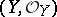 if
if 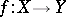 is a continuous mapping and
is a continuous mapping and 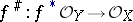 is a homomorphism of sheaves of rings over
is a homomorphism of sheaves of rings over 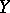 which transfers units in the stalks to units. Ringed spaces and their morphisms constitute a category. Giving a homomorphism
which transfers units in the stalks to units. Ringed spaces and their morphisms constitute a category. Giving a homomorphism 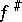 is equivalent to giving a homomorphism
is equivalent to giving a homomorphism
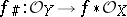 |
which transfers unit elements to unit elements.
A ringed space 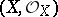 is called a local ringed space if
is called a local ringed space if 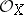 is a sheaf of local rings (cf. Local ring). In defining a morphism
is a sheaf of local rings (cf. Local ring). In defining a morphism 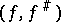 between local ringed spaces
between local ringed spaces 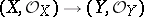 it is further assumed that for any
it is further assumed that for any 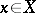 , the homomorphism
, the homomorphism
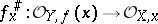 |
is local. Local ringed spaces form a subcategory in the category of all ringed spaces. Another important subcategory is that of ringed spaces over a (fixed) field 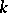 , i.e. ringed spaces
, i.e. ringed spaces 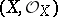 where
where 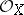 is a sheaf of algebras over
is a sheaf of algebras over 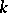 , while the morphisms are compatible with the structure of the algebras.
, while the morphisms are compatible with the structure of the algebras.
Examples of ringed spaces.
1) For each topological space 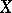 there is a corresponding ringed space
there is a corresponding ringed space 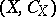 , where
, where 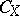 is the sheaf of germs of continuous functions on
is the sheaf of germs of continuous functions on 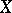 .
.
2) For each differentiable manifold 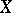 (e.g. of class
(e.g. of class 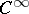 ) there is a corresponding ringed space
) there is a corresponding ringed space 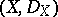 , where
, where 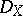 is the sheaf of germs of functions of class
is the sheaf of germs of functions of class 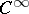 on
on 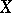 ; moreover, the category of differentiable manifolds is a full subcategory of the category of ringed spaces over
; moreover, the category of differentiable manifolds is a full subcategory of the category of ringed spaces over 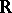 .
.
3) The analytic manifolds (cf. Analytic manifold) and analytic spaces (cf. Analytic space) over a field 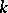 constitute full subcategories of the category of ringed spaces over
constitute full subcategories of the category of ringed spaces over 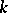 .
.
4) Schemes (cf. Scheme) constitute a full subcategory of the category of local ringed spaces.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
| [2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
Comments
If 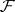 is a sheaf over a topological space
is a sheaf over a topological space 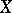 and
and 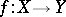 is a mapping of topological spaces, then the induced sheaf
is a mapping of topological spaces, then the induced sheaf 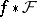 over
over  is the sheaf defined by
is the sheaf defined by 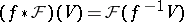 for all open
for all open 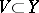 .
.
Ringed space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ringed_space&oldid=30763