Riesz-Fischer theorem
From Encyclopedia of Mathematics
A theorem establishing a relationship between the spaces 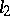 and
and 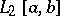 : If a system of functions
: If a system of functions 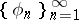 is orthonormal on the interval
is orthonormal on the interval 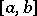 (cf. Orthonormal system) and a sequence of numbers
(cf. Orthonormal system) and a sequence of numbers 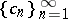 is such that
is such that
 |
(that is, 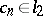 ), then there exists a function
), then there exists a function 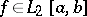 for which
for which
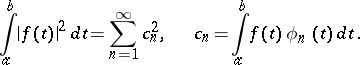 |
Moreover, the function 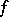 is unique as an element of the space
is unique as an element of the space 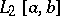 , i.e. up to its values on a set of Lebesgue measure zero. In particular, if the orthonormal system
, i.e. up to its values on a set of Lebesgue measure zero. In particular, if the orthonormal system 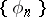 is closed (complete, cf. Complete system of functions) in
is closed (complete, cf. Complete system of functions) in  , then, using the Riesz–Fischer theorem, one gets that the spaces
, then, using the Riesz–Fischer theorem, one gets that the spaces 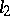 and
and 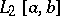 are isomorphic and isometric.
are isomorphic and isometric.
The theorem was proved independently by F. Riesz [1] and E. Fischer [2].
References
| [1] | F. Riesz, "Sur les systèmes orthogonaux de fonctions" C.R. Acad. Sci. Paris , 144 (1907) pp. 615–619 |
| [2] | E. Fischer, C.R. Acad. Sci. Paris , 144 (1907) pp. 1022–1024; 1148–1150 |
| [3] | I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian) |
Comments
References
| [a1] | R.V. Kadison, J.R. Ringrose, "Fundamentals of the theory of operator algebras" , 1 , Acad. Press (1983) |
How to Cite This Entry:
Riesz-Fischer theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riesz-Fischer_theorem&oldid=12351
Riesz-Fischer theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riesz-Fischer_theorem&oldid=12351
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article