Difference between revisions of "Riemann theta-function"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) pp. Chapt. 9 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.I. Markushevich, "Introduction to the classical theory of Abelian functions" , Moscow (1979) (In Russian) {{MR|0544988}} {{ZBL|0493.14023}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Krazer, "Lehrbuch der Thetafunktionen" , Chelsea, reprint (1970) {{MR|}} {{ZBL|0212.42901}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> F. Conforto, "Abelsche Funktionen und algebraische Geometrie" , Springer (1956) {{MR|0079316}} {{ZBL|0074.36601}} </TD></TR></table> |
| Line 36: | Line 36: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , '''1–2''' , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E. Arbarello, "Periods of Abelian integrals, theta functions, and differential equations of KdV type" , ''Proc. Internat. Congress Mathematicians (Berkeley, 1986)'' , '''I''' , Amer. Math. Soc. (1987) pp. 623–627 {{MR|0934264}} {{ZBL|0696.14019}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Mumford, "Tata lectures on Theta" , '''1–2''' , Birkhäuser (1983–1984) {{MR|2352717}} {{MR|2307769}} {{MR|2307768}} {{MR|1116553}} {{MR|0742776}} {{MR|0688651}} {{ZBL|1124.14043}} {{ZBL|1112.14003}} {{ZBL|1112.14002}} {{ZBL|0744.14033}} {{ZBL|0549.14014}} {{ZBL|0509.14049}} </TD></TR></table> |
Revision as of 21:56, 30 March 2012
A superposition of theta-functions (cf. Theta-function) of the first order  ,
,  , with half-integral characteristics
, with half-integral characteristics  , and of Abelian integrals (cf. Abelian integral) of the first order, used by B. Riemann in 1857 to solve the Jacobi inversion problem.
, and of Abelian integrals (cf. Abelian integral) of the first order, used by B. Riemann in 1857 to solve the Jacobi inversion problem.
Let  be an algebraic equation which defines a compact Riemann surface
be an algebraic equation which defines a compact Riemann surface  of genus
of genus  ; let
; let  be a basis of the Abelian differentials (cf. Abelian differential) of the first kind on
be a basis of the Abelian differentials (cf. Abelian differential) of the first kind on  with
with  -dimensional period matrix
-dimensional period matrix
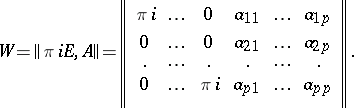 |
Let
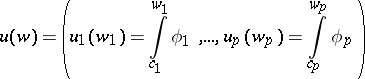 |
be the vector of basis Abelian integrals of the first kind, where 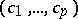 is a fixed system of points in
is a fixed system of points in 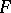 and
and 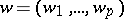 is a varying system of points in
is a varying system of points in 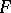 . For any theta-characteristic
. For any theta-characteristic
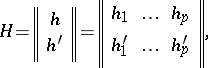 |
where the integers 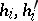 take the values 0 or 1 only, it is possible to construct a theta-function
take the values 0 or 1 only, it is possible to construct a theta-function  with period matrix
with period matrix  such that
such that 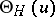 satisfies the fundamental relations
satisfies the fundamental relations
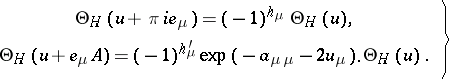 | (1) |
Here 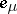 is the
is the 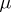 -th row vector of the identity matrix
-th row vector of the identity matrix  ,
, 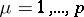 . If
. If  is a fixed vector in the complex space
is a fixed vector in the complex space 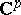 , then the Riemann theta-function
, then the Riemann theta-function  can be represented as the superposition
can be represented as the superposition
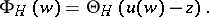 | (2) |
In the domain 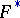 that is obtained from
that is obtained from  after removal of sections along the cycles
after removal of sections along the cycles  of a homology basis of
of a homology basis of 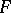 , the Riemann theta-functions (2) are everywhere defined and analytic. When crossing through sections the Riemann theta-functions, as a rule, are multiplied by factors whose values are determined from the fundamental relations (1). In this case, a special role is played by the theta-function of the first order
, the Riemann theta-functions (2) are everywhere defined and analytic. When crossing through sections the Riemann theta-functions, as a rule, are multiplied by factors whose values are determined from the fundamental relations (1). In this case, a special role is played by the theta-function of the first order  with zero characteristic
with zero characteristic 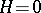 . In particular, the zeros
. In particular, the zeros 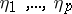 of the corresponding Riemann theta-function
of the corresponding Riemann theta-function 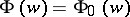 determine the solution to the Jacobi inversion problem.
determine the solution to the Jacobi inversion problem.
Quotients of Riemann theta-functions of the type 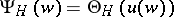 with a common denominator
with a common denominator 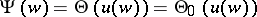 are used to construct analytic expressions solving the inversion problem. It can be seen from (1) that such quotients
are used to construct analytic expressions solving the inversion problem. It can be seen from (1) that such quotients 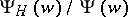 can have as non-trivial factors only
can have as non-trivial factors only  , and the squares of these quotients are single-valued meromorphic functions on
, and the squares of these quotients are single-valued meromorphic functions on 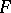 , i.e. rational point functions on the surface
, i.e. rational point functions on the surface 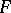 . The squares and other rational functions in quotients of theta-functions used in this case are special Abelian functions (cf. Abelian function) with
. The squares and other rational functions in quotients of theta-functions used in this case are special Abelian functions (cf. Abelian function) with 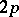 periods. The specialization is expressed by the fact that
periods. The specialization is expressed by the fact that 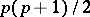 different elements
different elements 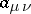 of the symmetric matrix
of the symmetric matrix 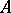 , when
, when 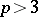 , are connected by definite relations imposed by the conformal structure of
, are connected by definite relations imposed by the conformal structure of 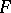 , so that
, so that 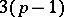 remain independent among them.
remain independent among them.
Riemann theta-functions constructed for a hyper-elliptic surface 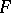 , when
, when 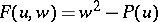 where
where 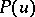 is a polynomial of degree
is a polynomial of degree 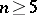 without multiple roots, are sometimes referred to as hyper-elliptic theta-functions.
without multiple roots, are sometimes referred to as hyper-elliptic theta-functions.
References
| [1] | N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) pp. Chapt. 9 (In Russian) |
| [2] | A.I. Markushevich, "Introduction to the classical theory of Abelian functions" , Moscow (1979) (In Russian) MR0544988 Zbl 0493.14023 |
| [3] | A. Krazer, "Lehrbuch der Thetafunktionen" , Chelsea, reprint (1970) Zbl 0212.42901 |
| [4] | F. Conforto, "Abelsche Funktionen und algebraische Geometrie" , Springer (1956) MR0079316 Zbl 0074.36601 |
Comments
Nowadays a Riemann theta-function is defined as a theta-function of the first order with half-integral characteristic corresponding to the Jacobi variety of an algebraic curve (or a compact Riemann surface). A general theta-function corresponds to an arbitrary Abelian variety. The problem of distinguishing the Riemann theta-functions among the general theta-functions is called the Schottky problem. It has been solved (see Schottky problem).
References
| [a1] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , 1–2 , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [a2] | E. Arbarello, "Periods of Abelian integrals, theta functions, and differential equations of KdV type" , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , I , Amer. Math. Soc. (1987) pp. 623–627 MR0934264 Zbl 0696.14019 |
| [a3] | D. Mumford, "Tata lectures on Theta" , 1–2 , Birkhäuser (1983–1984) MR2352717 MR2307769 MR2307768 MR1116553 MR0742776 MR0688651 Zbl 1124.14043 Zbl 1112.14003 Zbl 1112.14002 Zbl 0744.14033 Zbl 0549.14014 Zbl 0509.14049 |
Riemann theta-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_theta-function&oldid=16988