Rickart ring
(left), left 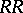 -ring
-ring
A ring in which the left annihilator of any element is generated by an idempotent (right Rickart rings are defined in a symmetric way). Rickart rings are characterized by the projectivity of all principal left (right) ideals. Regular, Baer and semi-hereditary rings are Rickart rings. A left Rickart ring need not be a right Rickart ring. A ring of matrices over a Rickart ring need not be a Rickart ring. The ring of endomorphisms of all free left  -modules is a Rickart ring if and only if
-modules is a Rickart ring if and only if  is left-hereditary. All these rings are right Rickart rings if and only if
is left-hereditary. All these rings are right Rickart rings if and only if  is left-hereditary, left-perfect and right-coherent. Under these conditions the rings of endomorphisms prove to be Baer rings (see Regular ring (in the sense of von Neumann)). A commutative ring
is left-hereditary, left-perfect and right-coherent. Under these conditions the rings of endomorphisms prove to be Baer rings (see Regular ring (in the sense of von Neumann)). A commutative ring  is a Rickart ring if and only if its full ring of fractions is regular in the sense of von Neumann and if for every maximal ideal
is a Rickart ring if and only if its full ring of fractions is regular in the sense of von Neumann and if for every maximal ideal  of
of  the ring of fractions
the ring of fractions  does not have zero divisors. A ring of polynomials over a commutative Rickart ring is a Rickart ring.
does not have zero divisors. A ring of polynomials over a commutative Rickart ring is a Rickart ring.
A ring with an involution  is called a Rickart
is called a Rickart  -ring if the left annihilator of any element is generated by a projection, i.e. by an element
-ring if the left annihilator of any element is generated by a projection, i.e. by an element  such that
such that  . The analogous property for right annihilators is automatically fulfilled in this case. The projections of a Rickart
. The analogous property for right annihilators is automatically fulfilled in this case. The projections of a Rickart  -ring form a lattice. This lattice is complete if and only if the annihilator of any set is generated by projections. Such rings are known as Baer
-ring form a lattice. This lattice is complete if and only if the annihilator of any set is generated by projections. Such rings are known as Baer  -rings. The term "Rickart ring" was introduced in honour of C.E. Rickart, who studied the corresponding property in rings of operators (see [1]).
-rings. The term "Rickart ring" was introduced in honour of C.E. Rickart, who studied the corresponding property in rings of operators (see [1]).
References
| [1] | C.E. Rickart, "Banach algebras with an adjoint operation" Ann. of Math. , 47 (1946) pp. 528–550 |
| [2] | S.K. Berberian, "Baer  -rings" , Springer (1972) -rings" , Springer (1972) |
| [3] | I. Kaplansky, "Rings of operators" , Benjamin (1968) |
| [4] | V.T. Markov, A.V. Mikhalev, L.A. Skornyakov, A.A. Tuganbaev, "Modules" J. Soviet Math. , 23 : 6 (1983) pp. 2642–2707 Itogi Nauk. i Tekn. Algebra Topol. Geom. , 19 (1981) pp. 31–134 |
Rickart ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rickart_ring&oldid=12174