Representation of a partially ordered set
Let  be a partially ordered set and
be a partially ordered set and  a field. Let
a field. Let  be a symbol with
be a symbol with  . An
. An  -space is of the form
-space is of the form  , where the
, where the  are subspaces of the
are subspaces of the  -space
-space  for
for  , such that
, such that 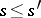 implies
implies  . Let
. Let  be
be 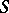 -spaces; a mapping
-spaces; a mapping 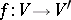 is a
is a  -linear mapping
-linear mapping 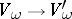 such that
such that 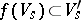 for all
for all 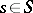 . The direct sum of
. The direct sum of  and
and 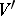 is
is 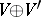 with
with 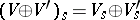 for all
for all  . An
. An 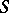 -space is said to be indecomposable if it cannot be written as the direct sum of two non-zero
-space is said to be indecomposable if it cannot be written as the direct sum of two non-zero 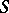 -spaces.
-spaces.
The partially ordered set  is called subspace-finite if there are only finitely many isomorphism classes of indecomposable
is called subspace-finite if there are only finitely many isomorphism classes of indecomposable 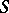 -spaces. Kleiner's theorem asserts that
-spaces. Kleiner's theorem asserts that 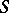 is subspace-finite if
is subspace-finite if 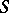 is finite and does not contain as a full subset one of the partially ordered sets
is finite and does not contain as a full subset one of the partially ordered sets
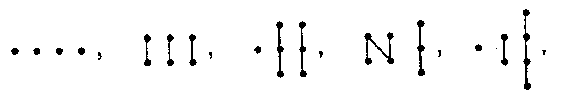
Figure: r081400a
see [a1]. M.M. Kleiner also has determined all the indecomposable representations of a representation-finite partially ordered set [a2]. A characterization of the tame partially ordered sets has been obtained by L.A. Nazarova [a3]. The representation theory of partially ordered sets plays a prominent role in the representation theory of finite-dimensional algebras.
References
| [a1] | M.M. Kleiner, "Partially ordered sets of finite type" J. Soviet Math. , 3 (1975) pp. 607–615 Zap. Nauchn. Sem. Leningr. Otdel. Mat. Inst. , 28 (1972) pp. 32–41 |
| [a2] | M.M. Kleiner, "On the exact representations of partially ordered sets of finite type" J. Soviet Math. , 3 (1975) pp. 616–628 Zap. Nauchn. Sem. Leningr. Otdel. Mat. Inst. , 28 (1972) pp. 42–60 |
| [a3] | L.A. Nazarova, "Partially ordered sets of infinite type" Math. USSR Izv. , 9 : 5 (1975) pp. 911–938 Izv. Akad. Nauk SSSR Ser. Mat. , 39 (1975) pp. 963–991 |
Representation of a partially ordered set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_a_partially_ordered_set&oldid=18218