Reinhardt domain
multiple-circled domain
A domain  in the complex space
in the complex space  ,
,  , with centre at a point
, with centre at a point  , with the following property: Together with any point
, with the following property: Together with any point  , the domain also contains the set
, the domain also contains the set
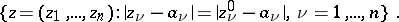 |
A Reinhardt domain  with
with  is invariant under the transformations
is invariant under the transformations  ,
, 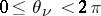 ,
,  . The Reinhardt domains constitute a subclass of the Hartogs domains (cf. Hartogs domain) and a subclass of the circular domains, which are defined by the following condition: Together with any
. The Reinhardt domains constitute a subclass of the Hartogs domains (cf. Hartogs domain) and a subclass of the circular domains, which are defined by the following condition: Together with any 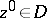 , the domain contains the set
, the domain contains the set
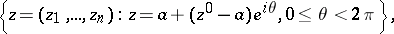 |
i.e. all points of the circle with centre  and radius
and radius 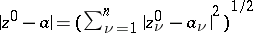 that lie on the complex line through
that lie on the complex line through  and
and 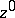 .
.
A Reinhardt domain 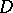 is called a complete Reinhardt domain if together with any point
is called a complete Reinhardt domain if together with any point 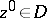 it also contains the polydisc
it also contains the polydisc
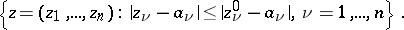 |
A complete Reinhardt domain is star-like with respect to its centre  (cf. Star-like domain).
(cf. Star-like domain).
Examples of complete Reinhardt domains are balls and polydiscs in  . A circular domain
. A circular domain 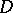 is called a complete circular domain if together with any pont
is called a complete circular domain if together with any pont  it also contains the entire disc
it also contains the entire disc  .
.
A Reinhardt domain  is called logarithmically convex if the image
is called logarithmically convex if the image 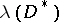 of the set
of the set
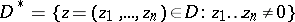 |
under the mapping
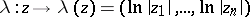 |
is a convex set in the real space  . An important property of logarithmically-convex Reinhardt domains is the following: Every such domain in
. An important property of logarithmically-convex Reinhardt domains is the following: Every such domain in  is the interior of the set of points of absolute convergence (i.e. the domain of convergence) of some power series in
is the interior of the set of points of absolute convergence (i.e. the domain of convergence) of some power series in  , and conversely: The domain of convergence of any power series in
, and conversely: The domain of convergence of any power series in  is a logarithmically-convex Reinhardt domain with centre
is a logarithmically-convex Reinhardt domain with centre  .
.
References
| [1] | V.S. Vladimirov, "Methods of the theory of functions of many complex variables" , M.I.T. (1966) (Translated from Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) (In Russian) |
Comments
The final paragraph reduces to: A Reinhardt domain is a domain of holomorphy if and only if it is logarithmically convex.
References
| [a1] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) |
| [a2] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) |
Reinhardt domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reinhardt_domain&oldid=16774