Difference between revisions of "Real algebraic variety"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48448 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r0800201.png" /> of real points of an [[Algebraic variety|algebraic variety]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r0800202.png" /> defined over the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r0800203.png" /> of real numbers. A real algebraic variety is said to be non-singular if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r0800204.png" /> is non-singular. In such a case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r0800205.png" /> is a smooth variety, and its dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r0800206.png" /> is equal to the dimension of the complex variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r0800207.png" />; the latter is known as the complexification of the variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r0800208.png" />. |
| − | r0800201.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Non-singular regular complete intersections have been most thoroughly studied. These are varieties <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r0800209.png" /> in the projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002010.png" /> which are non-singular regular intersections of hypersurfaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002012.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002013.png" /> is a homogeneous real polynomial in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002014.png" /> variables of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002015.png" />. In such a case the matrix | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002016.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | has rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002017.png" /> at all points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002018.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002019.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002020.png" /> denote the real algebraic variety defined as the intersection system | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002021.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Examples of regular complete intersections are: | Examples of regular complete intersections are: | ||
| − | 1) A plane real algebraic curve; here | + | 1) A plane real algebraic curve; here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002024.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002025.png" />. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 2) A real algebraic hypersurface; here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002028.png" />. In particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002029.png" />, a real algebraic surface is obtained. | |
| − | |||
| − | |||
| − | + | 3) A real algebraic space curve; here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002031.png" />. The surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002032.png" /> is defined by an equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002033.png" />, while the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002034.png" /> is cut out on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002035.png" /> by a surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002036.png" />. | |
| − | |||
| − | the | ||
| − | + | A real algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002037.png" /> of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002038.png" /> in the plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002039.png" /> consists of finitely many components diffeomorphic to a circle. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002040.png" /> is even, these components are all two-sidedly imbedded in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002041.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002042.png" /> is odd, one component is imbedded one-sidedly, while the remaining ones are imbedded two-sidedly. A two-sidedly imbedded component of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002043.png" /> is called an oval of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002044.png" />. An oval lying inside an odd number of other ovals of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002045.png" /> is called odd, while the remaining ovals are even. | |
| − | - | ||
| − | |||
| − | |||
| − | |||
| − | ( | + | The number of components of a plane real algebraic curve of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002046.png" /> is not larger than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002047.png" /> (Harnack's theorem) [[#References|[1]]]. For each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002048.png" /> there exists a plane real algebraic curve with this largest number of components — the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002050.png" />-curve. (For methods of constructing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002051.png" />-curves see [[#References|[1]]], [[#References|[2]]], [[#References|[3]]]; for a generalization of these results to include space curves, see [[#References|[2]]].) |
| − | |||
| − | + | D. Hilbert posed in 1900 the problem of studying the topology of real algebraic varieties, and also of the imbedding of real algebraic varieties into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002052.png" /> and of one real algebraic variety into another (Hilbert's 16th problem). He also pointed out difficult partial problems: the study of the mutual locations of the ovals of a sixth-order curve, and the topology and the imbedding of a real algebraic fourth-order surface into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002053.png" />. These partial problems have been solved [[#References|[12]]], [[#References|[13]]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | For a plane real algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002054.png" /> of even order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002055.png" /> the following exact inequality is valid: | |
| − | |||
| − | |||
| − | - | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002056.png" /></td> </tr></table> |
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002057.png" /> is the number of even ovals and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002058.png" /> is the number of odd ovals of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002059.png" /> (Petrovskii's theorem). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002060.png" /> is odd, a similar inequality is valid for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002061.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002062.png" /> is a straight line in general position [[#References|[4]]]. When these results are generalized to include the case of a real algebraic hypersurface of even order, the role of the difference <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002063.png" /> is played by the [[Euler characteristic|Euler characteristic]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002064.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002065.png" />, while if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002066.png" /> is odd, the role of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002067.png" /> is played by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002068.png" />. Thus, for a real algebraic hypersurface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002069.png" /> of even order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002070.png" />, |
| − | is the | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002071.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002072.png" /> is the number of terms of the polynomial | |
| − | |||
| − | is | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002073.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | of degree not higher than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002074.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002075.png" /> is odd, then for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002076.png" />, | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002077.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | [[#References|[5]]]. The following inequality is satisfied for a real algebraic space curve (in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002078.png" />) for even <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002079.png" />: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002080.png" /></td> </tr></table> | |
| − | - | ||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002081.png" /></td> </tr></table> | |
| − | (if | + | (if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002082.png" />, this estimate is exact [[#References|[6]]]). Petrovskii's theorem has been generalized to arbitrary real algebraic varieties . |
| − | this estimate is exact [[#References|[6]]]). Petrovskii's theorem has been generalized to arbitrary real algebraic varieties . | ||
| − | For a plane real algebraic | + | For a plane real algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002083.png" />-curve of even order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002084.png" /> the following congruence is valid: |
| − | curve of even order | ||
| − | the following congruence is valid: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002085.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[#References|[8]]], , [[#References|[13]]]. In proving this congruence ([[#References|[8]]], ), real algebraic varieties were studied by methods of differential topology in a form which opened the way for further investigations. Let the plane real algebraic curve | + | [[#References|[8]]], , [[#References|[13]]]. In proving this congruence ([[#References|[8]]], ), real algebraic varieties were studied by methods of differential topology in a form which opened the way for further investigations. Let the plane real algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002086.png" /> have even order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002087.png" /> and let the sign of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002088.png" /> be chosen so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002089.png" /> is orientable, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002090.png" /> denote, respectively, the number of ovals of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002091.png" /> which externally bound the components of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002092.png" /> with positive, zero and negative Euler characteristics. In a similar manner, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002093.png" /> are the numbers of such odd ovals for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002094.png" />. Then [[#References|[8]]], [[#References|[3]]], |
| − | have even order | ||
| − | and let the sign of | ||
| − | be chosen so that | ||
| − | is orientable, while | ||
| − | denote, respectively, the number of ovals of | ||
| − | which externally bound the components of the set | ||
| − | with positive, zero and negative Euler characteristics. In a similar manner, | ||
| − | are the numbers of such odd ovals for | ||
| − | Then [[#References|[8]]], [[#References|[3]]], | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002095.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002096.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002097.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002098.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r08002099.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | For an arbitrary real algebraic variety in a | + | For an arbitrary real algebraic variety in a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020100.png" />-dimensional projective space the following inequality is valid: |
| − | dimensional projective space the following inequality is valid: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020101.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020102.png" /> is the homology space of the variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020103.png" /> with coefficients in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020104.png" /> . This inequality is a generalization of Harnack's theorem. If |
| − | is the homology space of the variety | ||
| − | with coefficients in | ||
| − | This inequality is a generalization of Harnack's theorem. If | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020105.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020106.png" /> is always an integer, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020107.png" /> is said to be an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020108.png" />-variety. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020109.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020110.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020111.png" />-variety. |
| − | is always an integer, | ||
| − | is said to be an | ||
| − | variety. If | ||
| − | |||
| − | is an | ||
| − | variety. | ||
The validity of the following congruences has been demonstrated: | The validity of the following congruences has been demonstrated: | ||
| − | A) For an | + | A) For an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020112.png" />-variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020113.png" /> and for even <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020114.png" />: |
| − | variety | ||
| − | and for even | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020115.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020116.png" /> is the [[Signature|signature]] of the variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020117.png" /> . |
| − | is the [[Signature|signature]] of the variety | ||
| − | B) For an | + | B) For an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020118.png" />-variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020119.png" /> and even <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020120.png" /> ([[#References|[13]]]): |
| − | variety | ||
| − | and even | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020121.png" /></td> </tr></table> | |
| − | |||
| − | |||
cf. the overview [[#References|[3]]]. | cf. the overview [[#References|[3]]]. | ||
| − | C) For a regular complete intersection, if | + | C) For a regular complete intersection, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020122.png" /> is even, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020123.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020124.png" />-variety and the inclusion homomorphism |
| − | is even, | ||
| − | is an | ||
| − | variety and the inclusion homomorphism | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020125.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
is zero, then | is zero, then | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020126.png" /></td> </tr></table> | |
| − | |||
| − | |||
and | and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020127.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | In this case, if | + | In this case, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020128.png" /> is even, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020129.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020130.png" />-variety and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020131.png" /> is zero ([[#References|[11]]]): |
| − | is even, | ||
| − | is an | ||
| − | variety and | ||
| − | is zero ([[#References|[11]]]): | ||
| − | if | + | if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020132.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020133.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020134.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020135.png" />, |
| − | |||
| − | |||
| − | |||
| − | if | + | if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020136.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020137.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020138.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020139.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020140.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020141.png" />, |
| − | |||
| − | |||
| − | |||
| − | or | ||
| − | |||
| − | if | + | if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020142.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020143.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020144.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020145.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020146.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020147.png" />. |
| − | > | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | or | ||
| − | |||
| − | In particular, for a real algebraic surface | + | In particular, for a real algebraic surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020148.png" /> of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020149.png" />, |
| − | of order | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020150.png" /></td> </tr></table> | |
| − | |||
| − | - | ||
| − | |||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020151.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020152.png" />-surface, then |
| − | is an | ||
| − | surface, then | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020153.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020154.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020155.png" />-surface, then |
| − | is an | ||
| − | surface, then | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020156.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020157.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020158.png" />-surface and contracts to a point in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020159.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020160.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020161.png" /> and |
| − | is an | ||
| − | surface and contracts to a point in | ||
| − | then | ||
| − | |||
| − | and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020162.png" /></td> </tr></table> | |
| − | |||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020163.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020164.png" />-surface and contracts to a point in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020165.png" />, then |
| − | is an | ||
| − | surface and contracts to a point in | ||
| − | then | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020166.png" /></td> </tr></table> | |
| − | |||
| − | Certain congruences have also been proved , [[#References|[13]]] for odd | + | Certain congruences have also been proved , [[#References|[13]]] for odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020167.png" />. In particular, for a plane real algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020168.png" /> which is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020169.png" />-curve of even order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020170.png" />: |
| − | In particular, for a plane real algebraic curve | ||
| − | which is an | ||
| − | curve of even order | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020171.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Certain results have also been obtained [[#References|[13]]] for real algebraic varieties with singularities. For an interesting approach to the study of real algebraic varieties see [[#References|[14]]]. | Certain results have also been obtained [[#References|[13]]] for real algebraic varieties with singularities. For an interesting approach to the study of real algebraic varieties see [[#References|[14]]]. | ||
| Line 381: | Line 139: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Harnack, "Ueber die Vieltheitigkeit der ebenen algebraischen Kurven" ''Math. Ann.'' , '''10''' (1876) pp. 189–198</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Hilbert, "Ueber die reellen Züge algebraischer Kurven" ''Math. Ann.'' , '''38''' (1891) pp. 115–138</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D. Hilbert, "Mathematische Probleme" ''Arch. Math. Phys.'' , '''1''' (1901) pp. 213–237 {{MR|}} {{ZBL|32.0084.05}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.G. Petrovskii, "On the topology of real plane algebraic curves" ''Ann. of Math.'' , '''39''' : 1 (1938) pp. 189–209 {{MR|1503398}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> O.A. Oleinik, I.G. Petrovskii, "On the topology of real algebraic surfaces" ''Transl. Amer. Math. Soc.'' , '''7''' (1952) pp. 399–417 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''13''' (1949) pp. 389–402 {{MR|0048095}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> O.A. Oleinik, "On the topology of real algebraic curves on an algebraic surface" ''Mat. Sb.'' , '''29''' (1951) pp. 133–156 (In Russian) {{MR|44863}} {{ZBL|}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> , ''Hilbert problems'' , Moscow (1969) (In Russian) {{MR|}} {{ZBL|0187.35502}} {{ZBL|0186.18601}} {{ZBL|0181.15503}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V.I. Arnol'd, "Distribution of the ovals of the real plane of algebraic curves, of involutions of four-dimensional smooth manifolds, and the arithmetic of integer-valued quadratic forms" ''Funct. Anal. Appl.'' , '''5''' : 3 (1971) pp. 169–176 ''Funkts. Anal.'' , '''5''' : 3 (1971) pp. 1–9 {{MR|}} {{ZBL|0268.53001}} </TD></TR><TR><TD valign="top">[9a]</TD> <TD valign="top"> V.A. Rokhlin, "Congruences modulo 16 in Hilbert's sixteenth problem" ''Funct. Anal. Appl.'' , '''6''' : 4 (1972) pp. 301–306 ''Funkts. Anal.'' , '''6''' : 4 (1972) pp. 58–64</TD></TR><TR><TD valign="top">[9b]</TD> <TD valign="top"> V.A. Rokhlin, "Congruences modulo 16 in Hilbert's sixteenth problem" ''Funct. Anal. Appl.'' , '''7''' : 2 (1973) pp. 163–165 ''Funkts. Anal.'' , '''7''' : 2 (1973) pp. 91–92</TD></TR><TR><TD valign="top">[10a]</TD> <TD valign="top"> V.M. Kharlamov, "A generalized Petrovskii inequality" ''Funct. Anal. Appl.'' , '''8''' : 2 (1974) pp. 132–137 ''Funkts. Anal.'' , '''8''' : 2 (1974) pp. 50–56 {{MR|}} {{ZBL|0301.14021}} </TD></TR><TR><TD valign="top">[10b]</TD> <TD valign="top"> V.M. Kharlamov, "A generalized Petrovskii inequality II" ''Funct. Anal. Appl.'' , '''9''' : 3 (1975) pp. 266–268 ''Funkts. Anal.'' , '''9''' : 3 (1975) pp. 93–94</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> V.M. Kharlamov, "Additive congruences for the Euler characteristic of real algebraic manifolds of even dimensions" ''Funct. Anal. Appl.'' , '''9''' : 2 (1975) pp. 134–141 ''Funkts. Anal.'' , '''9''' : 2 (1975) pp. 51–60</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> V.M. Kharlamov, "The topological type of nonsingular surfaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020172.png" /> of degree four" ''Funct. Anal. Appl.'' , '''10''' : 4 (1976) pp. 295–304 ''Funkts. Anal.'' , '''10''' : 4 (1976) pp. 55–68 {{MR|}} {{ZBL|0362.14013}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> D.A. Gudkov, "The topology of real projective algebraic varieties" ''Russian Math. Surveys'' , '''29''' : 4 (1974) pp. 1–80 ''Uspekhi Mat. Nauk'' , '''29''' : 4 (1974) pp. 3–79 {{MR|0399085}} {{ZBL|0316.14018}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> D. Sullivan, "Geometric topology" , '''I. Localization, periodicity, and Galois symmetry''' , M.I.T. (1971) {{MR|0494074}} {{MR|0494075}} {{ZBL|1078.55001}} {{ZBL|0871.57021}} {{ZBL|0366.57003}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Harnack, "Ueber die Vieltheitigkeit der ebenen algebraischen Kurven" ''Math. Ann.'' , '''10''' (1876) pp. 189–198</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Hilbert, "Ueber die reellen Züge algebraischer Kurven" ''Math. Ann.'' , '''38''' (1891) pp. 115–138</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D. Hilbert, "Mathematische Probleme" ''Arch. Math. Phys.'' , '''1''' (1901) pp. 213–237 {{MR|}} {{ZBL|32.0084.05}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.G. Petrovskii, "On the topology of real plane algebraic curves" ''Ann. of Math.'' , '''39''' : 1 (1938) pp. 189–209 {{MR|1503398}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> O.A. Oleinik, I.G. Petrovskii, "On the topology of real algebraic surfaces" ''Transl. Amer. Math. Soc.'' , '''7''' (1952) pp. 399–417 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''13''' (1949) pp. 389–402 {{MR|0048095}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> O.A. Oleinik, "On the topology of real algebraic curves on an algebraic surface" ''Mat. Sb.'' , '''29''' (1951) pp. 133–156 (In Russian) {{MR|44863}} {{ZBL|}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> , ''Hilbert problems'' , Moscow (1969) (In Russian) {{MR|}} {{ZBL|0187.35502}} {{ZBL|0186.18601}} {{ZBL|0181.15503}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V.I. Arnol'd, "Distribution of the ovals of the real plane of algebraic curves, of involutions of four-dimensional smooth manifolds, and the arithmetic of integer-valued quadratic forms" ''Funct. Anal. Appl.'' , '''5''' : 3 (1971) pp. 169–176 ''Funkts. Anal.'' , '''5''' : 3 (1971) pp. 1–9 {{MR|}} {{ZBL|0268.53001}} </TD></TR><TR><TD valign="top">[9a]</TD> <TD valign="top"> V.A. Rokhlin, "Congruences modulo 16 in Hilbert's sixteenth problem" ''Funct. Anal. Appl.'' , '''6''' : 4 (1972) pp. 301–306 ''Funkts. Anal.'' , '''6''' : 4 (1972) pp. 58–64</TD></TR><TR><TD valign="top">[9b]</TD> <TD valign="top"> V.A. Rokhlin, "Congruences modulo 16 in Hilbert's sixteenth problem" ''Funct. Anal. Appl.'' , '''7''' : 2 (1973) pp. 163–165 ''Funkts. Anal.'' , '''7''' : 2 (1973) pp. 91–92</TD></TR><TR><TD valign="top">[10a]</TD> <TD valign="top"> V.M. Kharlamov, "A generalized Petrovskii inequality" ''Funct. Anal. Appl.'' , '''8''' : 2 (1974) pp. 132–137 ''Funkts. Anal.'' , '''8''' : 2 (1974) pp. 50–56 {{MR|}} {{ZBL|0301.14021}} </TD></TR><TR><TD valign="top">[10b]</TD> <TD valign="top"> V.M. Kharlamov, "A generalized Petrovskii inequality II" ''Funct. Anal. Appl.'' , '''9''' : 3 (1975) pp. 266–268 ''Funkts. Anal.'' , '''9''' : 3 (1975) pp. 93–94</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> V.M. Kharlamov, "Additive congruences for the Euler characteristic of real algebraic manifolds of even dimensions" ''Funct. Anal. Appl.'' , '''9''' : 2 (1975) pp. 134–141 ''Funkts. Anal.'' , '''9''' : 2 (1975) pp. 51–60</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> V.M. Kharlamov, "The topological type of nonsingular surfaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080020/r080020172.png" /> of degree four" ''Funct. Anal. Appl.'' , '''10''' : 4 (1976) pp. 295–304 ''Funkts. Anal.'' , '''10''' : 4 (1976) pp. 55–68 {{MR|}} {{ZBL|0362.14013}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> D.A. Gudkov, "The topology of real projective algebraic varieties" ''Russian Math. Surveys'' , '''29''' : 4 (1974) pp. 1–80 ''Uspekhi Mat. Nauk'' , '''29''' : 4 (1974) pp. 3–79 {{MR|0399085}} {{ZBL|0316.14018}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> D. Sullivan, "Geometric topology" , '''I. Localization, periodicity, and Galois symmetry''' , M.I.T. (1971) {{MR|0494074}} {{MR|0494075}} {{ZBL|1078.55001}} {{ZBL|0871.57021}} {{ZBL|0366.57003}} </TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| + | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> O. Viro, "Successes of the last five years in the topology of real algebraic varieties" , ''Proc. Internat. Congress Mathematicians (Warszawa, 1983)'' , PWN & North-Holland (1984) pp. 603–619</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G. Wilson, "Hilbert's sixteenth problem" ''Topology'' , '''17''' (1978) pp. 53–74</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> O. Viro, "Successes of the last five years in the topology of real algebraic varieties" , ''Proc. Internat. Congress Mathematicians (Warszawa, 1983)'' , PWN & North-Holland (1984) pp. 603–619</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G. Wilson, "Hilbert's sixteenth problem" ''Topology'' , '''17''' (1978) pp. 53–74</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
The set 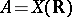 of real points of an algebraic variety
of real points of an algebraic variety 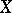 defined over the field
defined over the field 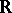 of real numbers. A real algebraic variety is said to be non-singular if
of real numbers. A real algebraic variety is said to be non-singular if 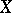 is non-singular. In such a case
is non-singular. In such a case 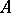 is a smooth variety, and its dimension
is a smooth variety, and its dimension 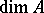 is equal to the dimension of the complex variety
is equal to the dimension of the complex variety  ; the latter is known as the complexification of the variety
; the latter is known as the complexification of the variety  .
.
Non-singular regular complete intersections have been most thoroughly studied. These are varieties 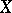 in the projective space
in the projective space 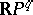 which are non-singular regular intersections of hypersurfaces
which are non-singular regular intersections of hypersurfaces 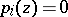 ,
, 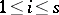 , where
, where 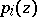 is a homogeneous real polynomial in
is a homogeneous real polynomial in 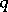 variables of degree
variables of degree 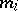 . In such a case the matrix
. In such a case the matrix
 |
has rank  at all points
at all points 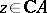 ;
; 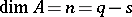 .
.
Let 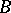 denote the real algebraic variety defined as the intersection system
denote the real algebraic variety defined as the intersection system
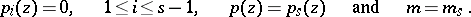 |
Examples of regular complete intersections are:
1) A plane real algebraic curve; here 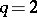 ,
, 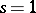 ,
, 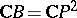 ,
, 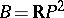 .
.
2) A real algebraic hypersurface; here 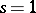 ,
, 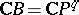 ,
, 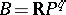 . In particular, if
. In particular, if 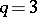 , a real algebraic surface is obtained.
, a real algebraic surface is obtained.
3) A real algebraic space curve; here 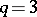 ,
, 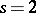 . The surface
. The surface 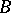 is defined by an equation
is defined by an equation 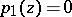 , while the curve
, while the curve 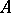 is cut out on
is cut out on 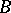 by a surface
by a surface 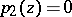 .
.
A real algebraic curve 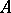 of order
of order 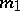 in the plane
in the plane 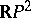 consists of finitely many components diffeomorphic to a circle. If
consists of finitely many components diffeomorphic to a circle. If 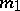 is even, these components are all two-sidedly imbedded in
is even, these components are all two-sidedly imbedded in 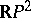 ; if
; if 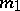 is odd, one component is imbedded one-sidedly, while the remaining ones are imbedded two-sidedly. A two-sidedly imbedded component of
is odd, one component is imbedded one-sidedly, while the remaining ones are imbedded two-sidedly. A two-sidedly imbedded component of 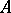 is called an oval of
is called an oval of 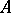 . An oval lying inside an odd number of other ovals of
. An oval lying inside an odd number of other ovals of 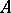 is called odd, while the remaining ovals are even.
is called odd, while the remaining ovals are even.
The number of components of a plane real algebraic curve of order 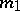 is not larger than
is not larger than 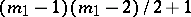 (Harnack's theorem) [1]. For each
(Harnack's theorem) [1]. For each 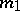 there exists a plane real algebraic curve with this largest number of components — the
there exists a plane real algebraic curve with this largest number of components — the 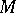 -curve. (For methods of constructing
-curve. (For methods of constructing 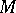 -curves see [1], [2], [3]; for a generalization of these results to include space curves, see [2].)
-curves see [1], [2], [3]; for a generalization of these results to include space curves, see [2].)
D. Hilbert posed in 1900 the problem of studying the topology of real algebraic varieties, and also of the imbedding of real algebraic varieties into 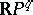 and of one real algebraic variety into another (Hilbert's 16th problem). He also pointed out difficult partial problems: the study of the mutual locations of the ovals of a sixth-order curve, and the topology and the imbedding of a real algebraic fourth-order surface into
and of one real algebraic variety into another (Hilbert's 16th problem). He also pointed out difficult partial problems: the study of the mutual locations of the ovals of a sixth-order curve, and the topology and the imbedding of a real algebraic fourth-order surface into 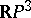 . These partial problems have been solved [12], [13].
. These partial problems have been solved [12], [13].
For a plane real algebraic curve 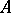 of even order
of even order 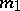 the following exact inequality is valid:
the following exact inequality is valid:
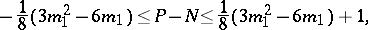 |
where 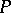 is the number of even ovals and
is the number of even ovals and 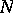 is the number of odd ovals of
is the number of odd ovals of  (Petrovskii's theorem). If
(Petrovskii's theorem). If 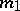 is odd, a similar inequality is valid for
is odd, a similar inequality is valid for 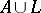 , where
, where 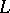 is a straight line in general position [4]. When these results are generalized to include the case of a real algebraic hypersurface of even order, the role of the difference
is a straight line in general position [4]. When these results are generalized to include the case of a real algebraic hypersurface of even order, the role of the difference 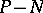 is played by the Euler characteristic
is played by the Euler characteristic 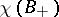 , where
, where 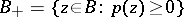 , while if
, while if 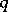 is odd, the role of
is odd, the role of 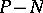 is played by
is played by 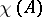 . Thus, for a real algebraic hypersurface
. Thus, for a real algebraic hypersurface 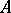 of even order
of even order 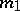 ,
,
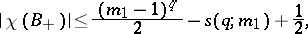 |
where 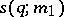 is the number of terms of the polynomial
is the number of terms of the polynomial
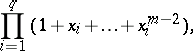 |
of degree not higher than 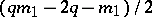 ; if
; if 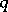 is odd, then for any
is odd, then for any 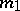 ,
,
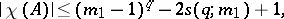 |
[5]. The following inequality is satisfied for a real algebraic space curve (in 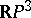 ) for even
) for even 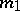 :
:
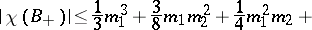 |
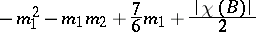 |
(if 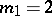 , this estimate is exact [6]). Petrovskii's theorem has been generalized to arbitrary real algebraic varieties .
, this estimate is exact [6]). Petrovskii's theorem has been generalized to arbitrary real algebraic varieties .
For a plane real algebraic 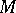 -curve of even order
-curve of even order 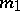 the following congruence is valid:
the following congruence is valid:
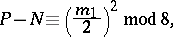 |
[8], , [13]. In proving this congruence ([8], ), real algebraic varieties were studied by methods of differential topology in a form which opened the way for further investigations. Let the plane real algebraic curve 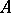 have even order
have even order 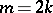 and let the sign of
and let the sign of 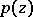 be chosen so that
be chosen so that 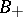 is orientable, while
is orientable, while 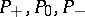 denote, respectively, the number of ovals of
denote, respectively, the number of ovals of 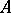 which externally bound the components of the set
which externally bound the components of the set 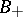 with positive, zero and negative Euler characteristics. In a similar manner,
with positive, zero and negative Euler characteristics. In a similar manner, 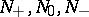 are the numbers of such odd ovals for
are the numbers of such odd ovals for 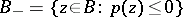 . Then [8], [3],
. Then [8], [3],
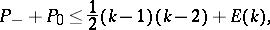 |
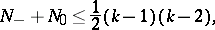 |
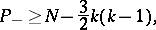 |
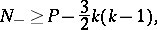 |
where
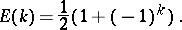 |
For an arbitrary real algebraic variety in a 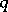 -dimensional projective space the following inequality is valid:
-dimensional projective space the following inequality is valid:
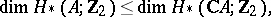 |
where 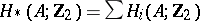 is the homology space of the variety
is the homology space of the variety 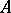 with coefficients in
with coefficients in 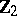 . This inequality is a generalization of Harnack's theorem. If
. This inequality is a generalization of Harnack's theorem. If
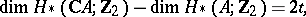 |
where 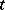 is always an integer,
is always an integer, 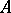 is said to be an
is said to be an 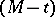 -variety. If
-variety. If  ,
, 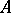 is an
is an 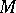 -variety.
-variety.
The validity of the following congruences has been demonstrated:
A) For an  -variety
-variety  and for even
and for even  :
:
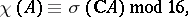 |
where 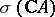 is the signature of the variety
is the signature of the variety 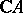 .
.
B) For an 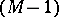 -variety
-variety 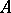 and even
and even  ([13]):
([13]):
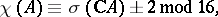 |
cf. the overview [3].
C) For a regular complete intersection, if  is even,
is even, 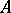 is an
is an  -variety and the inclusion homomorphism
-variety and the inclusion homomorphism
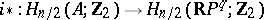 |
is zero, then
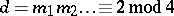 |
and
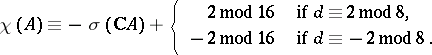 |
In this case, if  is even,
is even, 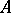 is an
is an 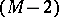 -variety and
-variety and 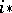 is zero ([11]):
is zero ([11]):
if 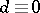
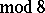 ,
, 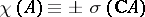
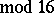 ,
,
if 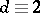
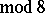 ,
, 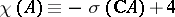
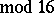 or
or 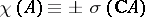
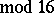 ,
,
if 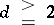
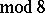 ,
, 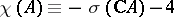
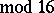 or
or 
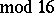 .
.
In particular, for a real algebraic surface 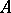 of order
of order 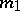 ,
,
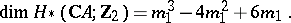 |
If 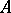 is an
is an 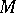 -surface, then
-surface, then
 |
If 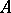 is an
is an  -surface, then
-surface, then
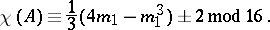 |
If 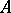 is an
is an 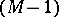 -surface and contracts to a point in
-surface and contracts to a point in 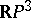 , then
, then 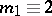
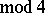 and
and
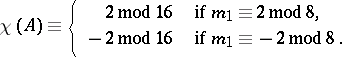 |
If  is an
is an 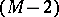 -surface and contracts to a point in
-surface and contracts to a point in 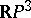 , then
, then
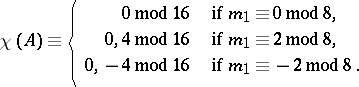 |
Certain congruences have also been proved , [13] for odd  . In particular, for a plane real algebraic curve
. In particular, for a plane real algebraic curve 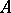 which is an
which is an 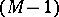 -curve of even order
-curve of even order 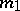 :
:
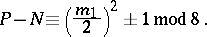 |
Certain results have also been obtained [13] for real algebraic varieties with singularities. For an interesting approach to the study of real algebraic varieties see [14].
References
| [1] | A. Harnack, "Ueber die Vieltheitigkeit der ebenen algebraischen Kurven" Math. Ann. , 10 (1876) pp. 189–198 |
| [2] | D. Hilbert, "Ueber die reellen Züge algebraischer Kurven" Math. Ann. , 38 (1891) pp. 115–138 |
| [3] | D. Hilbert, "Mathematische Probleme" Arch. Math. Phys. , 1 (1901) pp. 213–237 Zbl 32.0084.05 |
| [4] | I.G. Petrovskii, "On the topology of real plane algebraic curves" Ann. of Math. , 39 : 1 (1938) pp. 189–209 MR1503398 |
| [5] | O.A. Oleinik, I.G. Petrovskii, "On the topology of real algebraic surfaces" Transl. Amer. Math. Soc. , 7 (1952) pp. 399–417 Izv. Akad. Nauk SSSR Ser. Mat. , 13 (1949) pp. 389–402 MR0048095 |
| [6] | O.A. Oleinik, "On the topology of real algebraic curves on an algebraic surface" Mat. Sb. , 29 (1951) pp. 133–156 (In Russian) MR44863 |
| [7] | , Hilbert problems , Moscow (1969) (In Russian) Zbl 0187.35502 Zbl 0186.18601 Zbl 0181.15503 |
| [8] | V.I. Arnol'd, "Distribution of the ovals of the real plane of algebraic curves, of involutions of four-dimensional smooth manifolds, and the arithmetic of integer-valued quadratic forms" Funct. Anal. Appl. , 5 : 3 (1971) pp. 169–176 Funkts. Anal. , 5 : 3 (1971) pp. 1–9 Zbl 0268.53001 |
| [9a] | V.A. Rokhlin, "Congruences modulo 16 in Hilbert's sixteenth problem" Funct. Anal. Appl. , 6 : 4 (1972) pp. 301–306 Funkts. Anal. , 6 : 4 (1972) pp. 58–64 |
| [9b] | V.A. Rokhlin, "Congruences modulo 16 in Hilbert's sixteenth problem" Funct. Anal. Appl. , 7 : 2 (1973) pp. 163–165 Funkts. Anal. , 7 : 2 (1973) pp. 91–92 |
| [10a] | V.M. Kharlamov, "A generalized Petrovskii inequality" Funct. Anal. Appl. , 8 : 2 (1974) pp. 132–137 Funkts. Anal. , 8 : 2 (1974) pp. 50–56 Zbl 0301.14021 |
| [10b] | V.M. Kharlamov, "A generalized Petrovskii inequality II" Funct. Anal. Appl. , 9 : 3 (1975) pp. 266–268 Funkts. Anal. , 9 : 3 (1975) pp. 93–94 |
| [11] | V.M. Kharlamov, "Additive congruences for the Euler characteristic of real algebraic manifolds of even dimensions" Funct. Anal. Appl. , 9 : 2 (1975) pp. 134–141 Funkts. Anal. , 9 : 2 (1975) pp. 51–60 |
| [12] | V.M. Kharlamov, "The topological type of nonsingular surfaces in 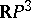 of degree four" Funct. Anal. Appl. , 10 : 4 (1976) pp. 295–304 Funkts. Anal. , 10 : 4 (1976) pp. 55–68 Zbl 0362.14013 of degree four" Funct. Anal. Appl. , 10 : 4 (1976) pp. 295–304 Funkts. Anal. , 10 : 4 (1976) pp. 55–68 Zbl 0362.14013 |
| [13] | D.A. Gudkov, "The topology of real projective algebraic varieties" Russian Math. Surveys , 29 : 4 (1974) pp. 1–80 Uspekhi Mat. Nauk , 29 : 4 (1974) pp. 3–79 MR0399085 Zbl 0316.14018 |
| [14] | D. Sullivan, "Geometric topology" , I. Localization, periodicity, and Galois symmetry , M.I.T. (1971) MR0494074 MR0494075 Zbl 1078.55001 Zbl 0871.57021 Zbl 0366.57003 |
Comments
References
| [a1] | O. Viro, "Successes of the last five years in the topology of real algebraic varieties" , Proc. Internat. Congress Mathematicians (Warszawa, 1983) , PWN & North-Holland (1984) pp. 603–619 |
| [a2] | G. Wilson, "Hilbert's sixteenth problem" Topology , 17 (1978) pp. 53–74 |
Real algebraic variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Real_algebraic_variety&oldid=49392