Difference between revisions of "Rayleigh-Taylor instability"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | r1100401.png | ||
| + | $#A+1 = 24 n = 0 | ||
| + | $#C+1 = 24 : ~/encyclopedia/old_files/data/R110/R.1100040 Rayleigh\ANDTaylor instability | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''of superposed fluids'' | ''of superposed fluids'' | ||
The instability of the interface between two fluids having different densities and accelerated towards each other [[#References|[a1]]], [[#References|[a2]]]. | The instability of the interface between two fluids having different densities and accelerated towards each other [[#References|[a1]]], [[#References|[a2]]]. | ||
| − | A static state in which an incompressible fluid of variable density subject to a vertical acceleration is arranged in horizontal strata and the pressure | + | A static state in which an incompressible fluid of variable density subject to a vertical acceleration is arranged in horizontal strata and the pressure $ p $ |
| + | and the density $ \rho $ | ||
| + | are functions of the vertical coordinate $ z $ | ||
| + | only, is clearly a kinematically realizable one. However, whether this state is also dynamically realizable is related to the issue of the stability under small disturbances. | ||
If viscosity is neglected, the flow can be assumed to be irrotational and the velocity potential of each fluid satisfies the [[Laplace equation|Laplace equation]]. The difficulty in solving this type of problem, however, arises from the non-linear boundary conditions at an unknown interface. On the other hand, if one assumes the disturbance amplitude to be infinitesimal, then the boundary conditions can be linearized and a solution of the linear problem can be readily obtained. | If viscosity is neglected, the flow can be assumed to be irrotational and the velocity potential of each fluid satisfies the [[Laplace equation|Laplace equation]]. The difficulty in solving this type of problem, however, arises from the non-linear boundary conditions at an unknown interface. On the other hand, if one assumes the disturbance amplitude to be infinitesimal, then the boundary conditions can be linearized and a solution of the linear problem can be readily obtained. | ||
| − | For the linear problem of two different inviscid and incompressible fluids separated by a plane interface and subject to an acceleration directed from the heavier fluid towards the lighter one, Lord Rayleigh [[#References|[a1]]] showed that the amplitude of a disturbance periodic in the horizontal interfacial plane will vary in time like | + | For the linear problem of two different inviscid and incompressible fluids separated by a plane interface and subject to an acceleration directed from the heavier fluid towards the lighter one, Lord Rayleigh [[#References|[a1]]] showed that the amplitude of a disturbance periodic in the horizontal interfacial plane will vary in time like $ e ^ {\sigma t } $, |
| + | where | ||
| − | + | $$ | |
| + | \sigma ^ {2} = { | ||
| + | \frac{\rho _ {2} - \rho _ {1} }{\rho _ {2} + \rho _ {1} } | ||
| + | } k, | ||
| + | $$ | ||
| − | where | + | where $ \rho _ {1} $ |
| + | and $ \rho _ {2} $ | ||
| + | are the respective densities of the lower and the upper fluids, $ k $ | ||
| + | is the horizontal wave-number of the disturbance, and $ g $ | ||
| + | is the gravitational acceleration. Thus, if $ \rho _ {1} > \rho _ {2} $, | ||
| + | then the interface is unstable. | ||
| − | R. Bellman and R. Pennington [[#References|[a3]]] showed that the effect of the surface tension | + | R. Bellman and R. Pennington [[#References|[a3]]] showed that the effect of the surface tension $ T $ |
| + | at the interface in the linear problem is to produce a critical wave-number $ k _ {c} $, | ||
| + | given by | ||
| − | + | $$ | |
| + | k _ {c} = \left [ { | ||
| + | \frac{g ( \rho _ {2} - \rho _ {1} ) }{T} | ||
| + | } \right ] ^ { {1 / 2 } } , | ||
| + | $$ | ||
| − | so the interface is unstable or stable according to whether the wave-number | + | so the interface is unstable or stable according to whether the wave-number $ k $ |
| + | is less than or greater than $ k _ {c} $. | ||
| + | The surface tension, therefore, has a stabilizing effect on the interface at sufficiently short wave-lengths. | ||
The predictions of the linear theory are well confirmed by laboratory experiments [[#References|[a4]]], [[#References|[a5]]], [[#References|[a6]]], [[#References|[a7]]], [[#References|[a8]]]. | The predictions of the linear theory are well confirmed by laboratory experiments [[#References|[a4]]], [[#References|[a5]]], [[#References|[a6]]], [[#References|[a7]]], [[#References|[a8]]]. | ||
| − | When the interface is unstable, according to the linear theory the evolution of the interface quickly gets out of the linear regime because the predicted growth is exponential. The non-linear problem in the neighbourhood of the linear stability threshold for the interface turns out to be a singular perturbation problem. One may, therefore, use the method of strained parameters to develop a uniformly valid solution for the above problem for wave-numbers near the linear cut-off value [[#References|[a9]]]. If the growth rate | + | When the interface is unstable, according to the linear theory the evolution of the interface quickly gets out of the linear regime because the predicted growth is exponential. The non-linear problem in the neighbourhood of the linear stability threshold for the interface turns out to be a singular perturbation problem. One may, therefore, use the method of strained parameters to develop a uniformly valid solution for the above problem for wave-numbers near the linear cut-off value [[#References|[a9]]]. If the growth rate $ \sigma $ |
| + | and the wave-number $ k $ | ||
| + | of the interfacial disturbance are expanded in powers of the initial interfacial disturbance amplitude $ \epsilon $ | ||
| + | as | ||
| − | + | $$ | |
| + | \sigma = \sigma _ {1} + \epsilon \sigma _ {2} + O ( \epsilon ^ {2} ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | k ^ {2} = k _ {c} ^ {2} + \epsilon ^ {2} k + O ( \epsilon ^ {3} ) , | ||
| + | $$ | ||
where, | where, | ||
| − | + | $$ | |
| + | k = k _ {c} : \sigma _ {1} = O, | ||
| + | $$ | ||
the non-linear problem leads to [[#References|[a9]]] | the non-linear problem leads to [[#References|[a9]]] | ||
| − | + | $$ | |
| + | k ^ {2} = k _ {c} ^ {2} + { | ||
| + | \frac{3}{8} | ||
| + | } { | ||
| + | \frac{\rho _ {2} g }{T \lambda _ {0} ^ {2} } | ||
| + | } \left ( 1 - { | ||
| + | \frac{\rho _ {1} }{\rho _ {2} } | ||
| + | } \right ) \epsilon ^ {2} + O ( \epsilon ^ {3} ) , | ||
| + | $$ | ||
| − | which is graphically represented in Fig.a1 ( | + | which is graphically represented in Fig.a1 ( $ \lambda _ {0} $ |
| + | being the wave-length of the initial interfacial disturbance). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r110040a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r110040a.gif" /> | ||
| Line 43: | Line 94: | ||
Linear and non-linear cut-offs for Rayleigh–Taylor instability | Linear and non-linear cut-offs for Rayleigh–Taylor instability | ||
| − | Observe that the interfacial disturbance grows even at | + | Observe that the interfacial disturbance grows even at $ k = k _ {c} $, |
| + | despite the cut-off predicted by the linear theory. On the other hand, the onset of instability even below the linear stability threshold when the disturbance has finite amplitude implies that this instability is a subcritical instability. | ||
For other aspects of Rayleigh–Taylor instability, as well as some recent developments, see [[#References|[a10]]], [[#References|[a11]]]. | For other aspects of Rayleigh–Taylor instability, as well as some recent developments, see [[#References|[a10]]], [[#References|[a11]]]. | ||
Latest revision as of 08:10, 6 June 2020
of superposed fluids
The instability of the interface between two fluids having different densities and accelerated towards each other [a1], [a2].
A static state in which an incompressible fluid of variable density subject to a vertical acceleration is arranged in horizontal strata and the pressure $ p $ and the density $ \rho $ are functions of the vertical coordinate $ z $ only, is clearly a kinematically realizable one. However, whether this state is also dynamically realizable is related to the issue of the stability under small disturbances.
If viscosity is neglected, the flow can be assumed to be irrotational and the velocity potential of each fluid satisfies the Laplace equation. The difficulty in solving this type of problem, however, arises from the non-linear boundary conditions at an unknown interface. On the other hand, if one assumes the disturbance amplitude to be infinitesimal, then the boundary conditions can be linearized and a solution of the linear problem can be readily obtained.
For the linear problem of two different inviscid and incompressible fluids separated by a plane interface and subject to an acceleration directed from the heavier fluid towards the lighter one, Lord Rayleigh [a1] showed that the amplitude of a disturbance periodic in the horizontal interfacial plane will vary in time like $ e ^ {\sigma t } $, where
$$ \sigma ^ {2} = { \frac{\rho _ {2} - \rho _ {1} }{\rho _ {2} + \rho _ {1} } } k, $$
where $ \rho _ {1} $ and $ \rho _ {2} $ are the respective densities of the lower and the upper fluids, $ k $ is the horizontal wave-number of the disturbance, and $ g $ is the gravitational acceleration. Thus, if $ \rho _ {1} > \rho _ {2} $, then the interface is unstable.
R. Bellman and R. Pennington [a3] showed that the effect of the surface tension $ T $ at the interface in the linear problem is to produce a critical wave-number $ k _ {c} $, given by
$$ k _ {c} = \left [ { \frac{g ( \rho _ {2} - \rho _ {1} ) }{T} } \right ] ^ { {1 / 2 } } , $$
so the interface is unstable or stable according to whether the wave-number $ k $ is less than or greater than $ k _ {c} $. The surface tension, therefore, has a stabilizing effect on the interface at sufficiently short wave-lengths.
The predictions of the linear theory are well confirmed by laboratory experiments [a4], [a5], [a6], [a7], [a8].
When the interface is unstable, according to the linear theory the evolution of the interface quickly gets out of the linear regime because the predicted growth is exponential. The non-linear problem in the neighbourhood of the linear stability threshold for the interface turns out to be a singular perturbation problem. One may, therefore, use the method of strained parameters to develop a uniformly valid solution for the above problem for wave-numbers near the linear cut-off value [a9]. If the growth rate $ \sigma $ and the wave-number $ k $ of the interfacial disturbance are expanded in powers of the initial interfacial disturbance amplitude $ \epsilon $ as
$$ \sigma = \sigma _ {1} + \epsilon \sigma _ {2} + O ( \epsilon ^ {2} ) , $$
$$ k ^ {2} = k _ {c} ^ {2} + \epsilon ^ {2} k + O ( \epsilon ^ {3} ) , $$
where,
$$ k = k _ {c} : \sigma _ {1} = O, $$
the non-linear problem leads to [a9]
$$ k ^ {2} = k _ {c} ^ {2} + { \frac{3}{8} } { \frac{\rho _ {2} g }{T \lambda _ {0} ^ {2} } } \left ( 1 - { \frac{\rho _ {1} }{\rho _ {2} } } \right ) \epsilon ^ {2} + O ( \epsilon ^ {3} ) , $$
which is graphically represented in Fig.a1 ( $ \lambda _ {0} $ being the wave-length of the initial interfacial disturbance).
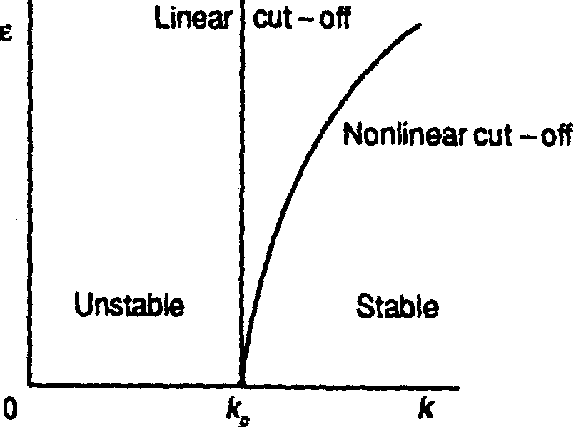
Figure: r110040a
Linear and non-linear cut-offs for Rayleigh–Taylor instability
Observe that the interfacial disturbance grows even at $ k = k _ {c} $, despite the cut-off predicted by the linear theory. On the other hand, the onset of instability even below the linear stability threshold when the disturbance has finite amplitude implies that this instability is a subcritical instability.
For other aspects of Rayleigh–Taylor instability, as well as some recent developments, see [a10], [a11].
References
| [a1] | Lord Rayleigh, "Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density" , Scientific Papers , II , Cambridge Univ. Press (1900) pp. 200–207 |
| [a2] | G.I. Taylor, "The stability of liquid surfaces when accelerated in a direction perpendicular to their planes" Proc. Roy. Soc. A , 201 (1950) pp. 192–196 |
| [a3] | R. Bellman, R. Pennington, "Effects of surface tension and viscosity on Taylor instability" Quart. Appl. Math. , 12 (1954) pp. 151–162 |
| [a4] | D.J. Lewis, "The instability of liquid surfaces when accelerated in a direction perpendicular to their planes" Proc. Roy. Soc. A , 202 (1950) pp. 81–96 |
| [a5] | R.E. Duff, F.H. Harlow, C.W. Hirt, "Effect of diffusion on interface instability between gases" Phys. Fluids , 5 (1962) pp. 417–425 |
| [a6] | H.W. Emmons, C.T. Chang, B.C. Watson, "Taylor instability of finite surface waves" J. Fluid Mech. , 7 (1960) pp. 177–193 |
| [a7] | M. Ratafia, "Experimental investigation of Rayleigh--Taylor instability" Phys. Fluids , 16 (1973) pp. 1207–1210 |
| [a8] | R.L. Cole, R.S. Tankin, "Experimental study of Taylor instability" Phys. Fluids , 16 (1973) pp. 1810–1815 |
| [a9] | B.K. Shivamoggi, "Nonlinear theory of Rayleigh–Taylor instability of superposed fluids" Acta Mech. , 31 (1979) pp. 301–305 |
| [a10] | D.H. Sharp, "An overview of Rayleigh–Taylor instability" Physica , 12D (1984) pp. 3–18 |
| [a11] | H. Kull, "Theory of the Rayleigh–Taylor instability" Phys. Rep. , 206 (1991) pp. 197–325 |
Rayleigh-Taylor instability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rayleigh-Taylor_instability&oldid=14084