Difference between revisions of "Rational variety"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (link) |
||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766010.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766010.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766011.png" /> is the canonical divisor of the algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766012.png" />, that is, the [[Kodaira dimension|Kodaira dimension]] of the rational variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766013.png" /> is equal to 0. | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766011.png" /> is the [[canonical divisor]] of the algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766012.png" />, that is, the [[Kodaira dimension|Kodaira dimension]] of the rational variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766013.png" /> is equal to 0. |
In low dimension the above invariants uniquely distinguish the class of rational varieties among all algebraic varieties. Thus, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766014.png" /> and the genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766015.png" /> is equal to 0, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766016.png" /> is a [[Rational curve|rational curve]]. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766017.png" />, the arithmetic genus | In low dimension the above invariants uniquely distinguish the class of rational varieties among all algebraic varieties. Thus, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766014.png" /> and the genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766015.png" /> is equal to 0, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766016.png" /> is a [[Rational curve|rational curve]]. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077660/r07766017.png" />, the arithmetic genus | ||
Revision as of 18:22, 19 October 2017
An algebraic variety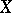 
, defined over an algebraically closed field 
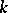, whose field of rational functions 
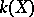is isomorphic to a purely transcendental extension of 
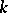of finite degree. In other words, a rational variety is an algebraic variety 
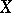that is birationally isomorphic to a projective space 
.
A complete smooth rational variety possesses the following birational invariants. The dimensions of all spaces 
of regular differential 
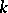-forms on 
are equal to 0. In addition, the multiple genus
 |
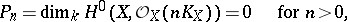where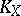 
is the canonical divisor of the algebraic variety 
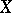, that is, the Kodaira dimension of the rational variety 
is equal to 0.
In low dimension the above invariants uniquely distinguish the class of rational varieties among all algebraic varieties. Thus, if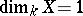 
and the genus of 
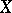is equal to 0, then 
is a rational curve. If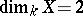 
, the arithmetic genus
 |
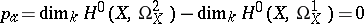and the multiple genus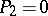 
, then 
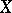is a rational surface. However, if 
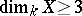, there is no good criterion of rationality, due to the negative solution of the Lüroth problem.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
Comments
References
| [a1] | A. Beauville, J.-L. Colliot-Hélène, J.J. Sansuc, P. Swinnerton-Dyer, "Variétés stablement rationelles non-rationelles" Ann. of Math. , 121 (1985) pp. 283–318 |
Rational variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_variety&oldid=23952