Difference between revisions of "Radical in a class of semi-groups"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48413 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r0771001.png" /> associating to each [[Semi-group|semi-group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r0771002.png" /> a congruence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r0771003.png" /> (cf. [[Congruence (in algebra)|Congruence (in algebra)]]) and having the following properties: 1) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r0771004.png" /> is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r0771005.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r0771006.png" /> (0 denotes the equality relation), then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r0771007.png" />; 2) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r0771008.png" /> is a congruence on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r0771009.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710010.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710011.png" />; and 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710012.png" />. If 1) and 3) are satisfied, then 2) is equivalent to |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | if | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710013.png" /></td> </tr></table> | |
| − | |||
| − | A | + | for every congruence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710014.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710015.png" />. A semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710016.png" /> is called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710018.png" />-semi-simple if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710019.png" />. The class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710020.png" />-semi-simple semi-groups contains the one-element semi-group and is closed relative to isomorphism and subdirect products. Conversely, each class of semi-groups having these properties is the class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710021.png" />-semi-simple semi-groups for some radical <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710022.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710023.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710024.png" /> is called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710026.png" />-radical. In contrast to rings, in semi-groups the radical is not determined by the corresponding radical class. If in the definition of a radical the discussion is limited to congruences defined by ideals, then another concept of a radical arises, where the corresponding function chooses an [[Ideal|ideal]] in each semi-group. |
| − | |||
| − | |||
| − | |||
| − | is | ||
| − | |||
| − | 0 | ||
| − | |||
| − | |||
| − | |||
| − | then | ||
| − | |||
| − | If | ||
| − | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710027.png" /> is a class of semi-groups that is closed relative to isomorphisms and that contains the one-element semi-group, then the function that associates to each semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710028.png" /> the intersection of all congruences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710029.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710030.png" /> turns out to be a radical, called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710031.png" />. The class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710032.png" /> coincides with the class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710033.png" />-semi-simple semi-groups if and only if it is closed relative to subdirect products. In this case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710034.png" /> is the largest quotient semi-group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710035.png" /> that lies in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710036.png" /> (see [[Replica|Replica]]). | |
| − | |||
| − | |||
| − | + | Example. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710037.png" /> be the class of semi-groups admitting a faithful irreducible representation (cf. [[Representation of a semi-group|Representation of a semi-group]]). Then | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710038.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710039.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710040.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | . | ||
| − | |||
Radicals defined on a given class of semi-groups that is closed relative to homomorphic images have been studied. | Radicals defined on a given class of semi-groups that is closed relative to homomorphic images have been studied. | ||
| − | Related to each radical | + | Related to each radical <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710041.png" /> is the class of left polygons <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710042.png" /> (cf. [[Polygon (over a monoid)|Polygon (over a monoid)]]). Namely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710043.png" /> is a left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710044.png" />-polygon, then a congruence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710045.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710046.png" /> is called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710048.png" />-annihilating if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710049.png" /> implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710050.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710051.png" />. The least upper bound of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710052.png" />-annihilating congruences turns out to be an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710053.png" />-annihilating congruence, and is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710054.png" />. The class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710055.png" />, by definition, consists of all left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710056.png" />-polygons <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710057.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710058.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710059.png" /> runs through the class of all semi-groups. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710060.png" /> is a congruence on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710061.png" />, then a left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710062.png" />-polygon lies in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710063.png" /> if and only if it lies in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710064.png" /> when considered as a left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710065.png" />-polygon. Conversely, if one is given a class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710066.png" /> of left polygons with these properties and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710067.png" /> is the class of all left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710068.png" />-polygons in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710069.png" />, then the function |
| − | is the class of left polygons | ||
| − | cf. [[Polygon (over a monoid)|Polygon (over a monoid)]]). Namely, if | ||
| − | is a left | ||
| − | polygon, then a congruence | ||
| − | on | ||
| − | is called | ||
| − | annihilating if | ||
| − | implies | ||
| − | for all | ||
| − | The least upper bound of all | ||
| − | annihilating congruences turns out to be an | ||
| − | annihilating congruence, and is denoted by | ||
| − | The class | ||
| − | by definition, consists of all left | ||
| − | polygons | ||
| − | such that | ||
| − | where | ||
| − | runs through the class of all semi-groups. If | ||
| − | is a congruence on | ||
| − | then a left | ||
| − | polygon lies in | ||
| − | if and only if it lies in | ||
| − | when considered as a left | ||
| − | polygon. Conversely, if one is given a class | ||
| − | of left polygons with these properties and if | ||
| − | is the class of all left | ||
| − | polygons in | ||
| − | then the function | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077100/r07710070.png" /></td> </tr></table> | |
| − | |||
| − | |||
is a radical. | is a radical. | ||
Revision as of 14:53, 7 June 2020
A function 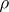 associating to each semi-group
associating to each semi-group 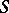 a congruence
a congruence 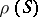 (cf. Congruence (in algebra)) and having the following properties: 1) if
(cf. Congruence (in algebra)) and having the following properties: 1) if 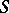 is isomorphic to
is isomorphic to 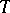 and
and 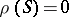 (0 denotes the equality relation), then
(0 denotes the equality relation), then  ; 2) if
; 2) if 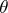 is a congruence on
is a congruence on 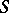 and
and 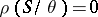 , then
, then 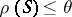 ; and 3)
; and 3)  . If 1) and 3) are satisfied, then 2) is equivalent to
. If 1) and 3) are satisfied, then 2) is equivalent to
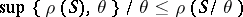 |
for every congruence 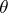 on
on 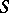 . A semi-group
. A semi-group 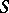 is called
is called 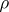 -semi-simple if
-semi-simple if 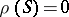 . The class of
. The class of  -semi-simple semi-groups contains the one-element semi-group and is closed relative to isomorphism and subdirect products. Conversely, each class of semi-groups having these properties is the class of
-semi-simple semi-groups contains the one-element semi-group and is closed relative to isomorphism and subdirect products. Conversely, each class of semi-groups having these properties is the class of 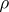 -semi-simple semi-groups for some radical
-semi-simple semi-groups for some radical 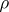 . If
. If 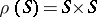 , then
, then 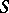 is called
is called 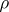 -radical. In contrast to rings, in semi-groups the radical is not determined by the corresponding radical class. If in the definition of a radical the discussion is limited to congruences defined by ideals, then another concept of a radical arises, where the corresponding function chooses an ideal in each semi-group.
-radical. In contrast to rings, in semi-groups the radical is not determined by the corresponding radical class. If in the definition of a radical the discussion is limited to congruences defined by ideals, then another concept of a radical arises, where the corresponding function chooses an ideal in each semi-group.
If 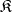 is a class of semi-groups that is closed relative to isomorphisms and that contains the one-element semi-group, then the function that associates to each semi-group
is a class of semi-groups that is closed relative to isomorphisms and that contains the one-element semi-group, then the function that associates to each semi-group 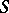 the intersection of all congruences
the intersection of all congruences 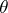 such that
such that 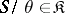 turns out to be a radical, called
turns out to be a radical, called 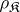 . The class
. The class 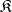 coincides with the class of
coincides with the class of 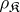 -semi-simple semi-groups if and only if it is closed relative to subdirect products. In this case
-semi-simple semi-groups if and only if it is closed relative to subdirect products. In this case  is the largest quotient semi-group of
is the largest quotient semi-group of 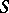 that lies in
that lies in 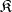 (see Replica).
(see Replica).
Example. Let 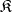 be the class of semi-groups admitting a faithful irreducible representation (cf. Representation of a semi-group). Then
be the class of semi-groups admitting a faithful irreducible representation (cf. Representation of a semi-group). Then
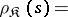 |
 |
where
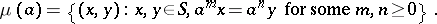 |
Radicals defined on a given class of semi-groups that is closed relative to homomorphic images have been studied.
Related to each radical  is the class of left polygons
is the class of left polygons  (cf. Polygon (over a monoid)). Namely, if
(cf. Polygon (over a monoid)). Namely, if  is a left
is a left 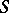 -polygon, then a congruence
-polygon, then a congruence 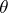 on
on 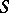 is called
is called  -annihilating if
-annihilating if  implies
implies 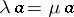 for all
for all 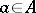 . The least upper bound of all
. The least upper bound of all  -annihilating congruences turns out to be an
-annihilating congruences turns out to be an 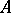 -annihilating congruence, and is denoted by
-annihilating congruence, and is denoted by  . The class
. The class 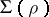 , by definition, consists of all left
, by definition, consists of all left 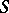 -polygons
-polygons 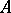 such that
such that  , where
, where 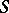 runs through the class of all semi-groups. If
runs through the class of all semi-groups. If 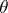 is a congruence on
is a congruence on 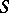 , then a left
, then a left 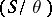 -polygon lies in
-polygon lies in  if and only if it lies in
if and only if it lies in 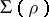 when considered as a left
when considered as a left 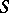 -polygon. Conversely, if one is given a class
-polygon. Conversely, if one is given a class 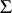 of left polygons with these properties and if
of left polygons with these properties and if 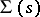 is the class of all left
is the class of all left 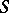 -polygons in
-polygons in 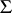 , then the function
, then the function
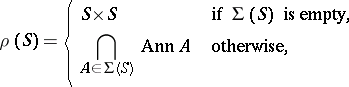 |
is a radical.
References
| [1] | A.H. Clifford, G.B. Preston, "The algebraic theory of semi-groups" , 2 , Amer. Math. Soc. (1967) |
| [2] | L.A. Skornyakov, "Radicals of  -rings" , Selected problems in algebra and logic , Novosibirsk (1973) pp. 283–299 (In Russian) -rings" , Selected problems in algebra and logic , Novosibirsk (1973) pp. 283–299 (In Russian) |
| [3] | A.H. Clifford, "Radicals in semigroups" Semigroup Forum , 1 : 2 (1970) pp. 103–127 |
| [4] | E.N. Roiz, B.M. Schein, "Radicals of semigroups" Semigroup Forum , 16 : 3 (1978) pp. 299–344 |
Radical in a class of semi-groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Radical_in_a_class_of_semi-groups&oldid=49387