Radiation conditions
Conditions at infinity for the uniqueness of a solution to exterior boundary value problems for equations of elliptic type (cf. Boundary value problem, elliptic equations), these being models of steady-state oscillations of various physical phenomena. The physical meaning of radiation conditions consists of the selection of the solution of the boundary value problem describing divergent waves with sources (real or fictitious) situated in a bounded domain (see [1]). The solutions of equations of steady-state oscillations describing waves with sources at infinity (for example, plane waves) do not satisfy radiation conditions.
The first analytic form of radiation conditions for the Helmholtz equation
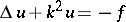 | (1) |
was proposed by A. Sommerfeld [2]. If (1) corresponds to the problem of stationary oscillations with time-dependence 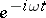 , then the corresponding radiation conditions have acquired the name Sommerfeld radiation conditions, and in the case of three-dimensional space they take the form
, then the corresponding radiation conditions have acquired the name Sommerfeld radiation conditions, and in the case of three-dimensional space they take the form
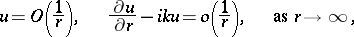 | (2) |
while in the two-dimensional case the Sommerfeld radiation conditions have the form
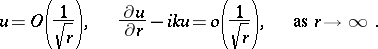 | (3) |
As was proved in [3], the first condition in (2) and (3) is a consequence of the second and the requirement that equation (1) be satisfied.
The conditions (2) and (3) can be weakened. In particular, (2) can in many cases be replaced by a non-local integral condition:
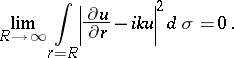 | (4) |
If the boundary of the exterior domain has points at infinity, conditions (2)–(4) are not universal in the sense that they do not always define a class of functions in which the corresponding boundary value problem has a unique solution. For example, there does not exist a classical solution of equation (1) with local right-hand side satisfying the Sommerfeld radiation conditions (2) or (4) in the layer between two parallel planes on which homogeneous Dirichlet or von Neumann boundary conditions are imposed (see [4]). For the problem to have a solution, these conditions must be replaced by the so-called partial radiation conditions (see [4]).
Unlike (2)–(4), partial radiation conditions cannot be stated in the form of asymptotic expressions, but as exact relations which must be satisfied by the components of the expansion of the solution in some system of basic functions. The corresponding system of basic functions is introduced in various ways, according to the specifics of the original boundary value problem. Thus, in the case of a boundary value problem for equation (1) with local right-hand side in the infinite cylinder with axis  , with homogeneous Dirichlet or von Neumann boundary conditions on the lateral surface of the cylinder, the partial radiation conditions can be written as
, with homogeneous Dirichlet or von Neumann boundary conditions on the lateral surface of the cylinder, the partial radiation conditions can be written as
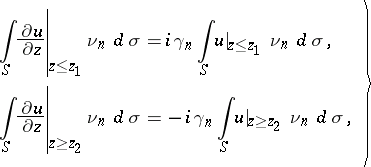 | (5) |
where 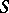 is a cross-section of the cylinder and the
is a cross-section of the cylinder and the 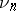 are the normalized eigen functions of the boundary value problem for the Laplace equation in
are the normalized eigen functions of the boundary value problem for the Laplace equation in 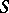 :
:
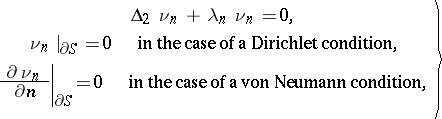 | (6) |
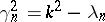 ,
, 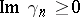 , and the support of the right-hand side lies in the domain bounded by the sections
, and the support of the right-hand side lies in the domain bounded by the sections 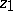 and
and 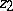 .
.
Since the analytic forms of the radiation conditions (2)–(5) are different, the question naturally arises as to the formulation of a general radiation principle that does not depend on the form of the unbounded domain in which the solution of the steady-state oscillation problem is sought. There are two possible approaches to the solution of this problem. In [5] the so-called limiting-amplitude principle is formulated, according to which the solution of the steady-state oscillation equation is determined uniquely by the requirement that it be the limit as 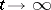 of the amplitude of the solution of the Cauchy problem with zero initial condition for the wave equation with periodic right-hand side, and in that article a proof of the limiting-amplitude principle is given for the problem of steady-state oscillations in every unbounded space. For a generalization of the limiting-amplitude principle to exterior problems for a fairly wide class of differential operators under certain additional conditions on the interior boundary of the unbounded domain see, for example, [6].
of the amplitude of the solution of the Cauchy problem with zero initial condition for the wave equation with periodic right-hand side, and in that article a proof of the limiting-amplitude principle is given for the problem of steady-state oscillations in every unbounded space. For a generalization of the limiting-amplitude principle to exterior problems for a fairly wide class of differential operators under certain additional conditions on the interior boundary of the unbounded domain see, for example, [6].
The other approach to the formulation of a general radiation principle, called the limit-absorption principle, consists of the fact that the solution of the exterior boundary value problem on steady-state oscillations in a medium without absorption is sought as the limit of the bounded solution of the corresponding boundary value problem in the medium with absorption, as the latter tends to zero. This method was first used to solve the concrete problem of the diffraction of electromagnetic waves by an infinitely-long wire (see ). There are generalizations of the limit-absorption principle as uniqueness conditions for the solution of exterior boundary value problems for general elliptic operators and for a fairly wide class of interior boundaries of the unbounded domain (see [8], for example).
The limiting-amplitude and limit-absorption principles are extensively used in the investigation of general properties of solutions of exterior boundary value problems; however, since, like the Sommerfeld radiation conditions (2)–(4), they have an asymptotic character, their use in the numerical solution of exterior boundary value problems turns out to be insufficiently effective in a number of cases. In these cases one commonly uses partial radiation conditions, which, combined with projection methods, have made it possible to carry out a complete numerical investigation of a large number of practically important problems (see [9], for example).
References
| [1] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) pp. Chapt. 1 (Translated from Russian) |
| [2] | A. Sommerfeld, "Die Greensche Funktion der Schwingungsgleichung" Jhrber. Deutsch. Math.-Verein , 21 (1912) pp. 309–353 |
| [3] | I.N. Vekua, "On metaharmonic functions" Trudy Tbiliss. Mat. Inst. , 12 (1943) pp. 105–174 (In Russian) |
| [4] | A.G. Sveshnikov, "The radiation principle" Dokl. Akad. Nauk SSSR , 73 : 5 (1950) pp. 917–920 (In Russian) |
| [5] | A.N. Tikhonov, A.A. Samarskii, "The radiation principle" Zh. Eksper. Teoret. Fiz. , 18 : 2 (1948) pp. 243–248 (In Russian) |
| [6] | P.D. Lax, R.S. Philips, "Scattering theory" , Acad. Press (1967) |
| [7a] | W. von [V.S. Ignatovskii] Ignatowsky, Ann. der Phys. , 18 : 13 (1905) pp. 495–522 |
| [7b] | W. von [V.S. Ignatovskii] Ignatowsky, Ann. der Phys. , 18 : 15 (1905) pp. 1078 |
| [8] | D.M. Eidus, "The principle of limit amplitude" Russian Math. Surveys , 24 : 3 (1969) pp. 97–167 Uspekhi Mat. Nauk , 24 : 3 (1969) pp. 91–156 |
| [9] | A.G. Sveshnikov, "Problems of mathematical physics and related questions in numerical mathematics and differential equations" , Moscow (1977) (In Russian) |
Comments
References
| [a1] | E. Zauderer, "Partial differential equations of applied mathematics" , Wiley (Interscience) (1989) |
| [a2] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
| [a3] | A.G. Ramm, "Scattering by obstacles" , Reidel (1986) |
| [a4] | G.B. Whitham, "Linear and non-linear waves" , Wiley (1974) |
Radiation conditions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Radiation_conditions&oldid=12637