The mathematical entities known as 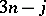 coefficients enter mathematics and physics in describing the reduction of the
coefficients enter mathematics and physics in describing the reduction of the 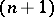 -fold Kronecker product of the unitary irreducible representations of the unitary unimodular group
-fold Kronecker product of the unitary irreducible representations of the unitary unimodular group 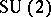 , the group of
, the group of 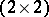 unitary unimodular matrices, into unitary irreducible representations of
unitary unimodular matrices, into unitary irreducible representations of 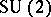 . This reduction has the form:
. This reduction has the form:
 | (a1) |
where the symbols and quantities entering this relation have the following definitions:
1) 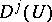 denotes the
denotes the 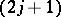 -dimensional unitary irreducible representation of
-dimensional unitary irreducible representation of 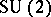 given explicitly below, where
given explicitly below, where  , and this label is called an irreducible representation label or an angular momentum quantum number.
, and this label is called an irreducible representation label or an angular momentum quantum number.
2)  denotes the matrix direct product (Kronecker product), and
denotes the matrix direct product (Kronecker product), and 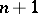 such products enter the left-hand side with arbitrary irreducible representation labels
such products enter the left-hand side with arbitrary irreducible representation labels 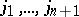 .
.
3)  denotes the matrix direct sum, and the direct sum on the right-hand side contains each irreducible representation
denotes the matrix direct sum, and the direct sum on the right-hand side contains each irreducible representation 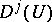 a number of times equal to
a number of times equal to
 | (a2) |
in which 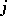 is any irreducible representation label given by
is any irreducible representation label given by
 | (a3) |
(see below). For an arbitrary triple 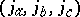 of irreducible representation labels, the quantity
of irreducible representation labels, the quantity 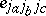 is
is  or
or 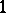 , and it is
, and it is 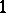 if and only if the so-called triangle conditions are satisfied:
if and only if the so-called triangle conditions are satisfied:
 | (a4) |
for 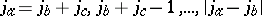 .
.
4) 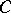 denotes a real orthogonal matrix of dimension
denotes a real orthogonal matrix of dimension 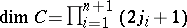 , with elements called Wigner–Clebsch–Gordan coefficients (WCG coefficients) for
, with elements called Wigner–Clebsch–Gordan coefficients (WCG coefficients) for 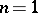 and generalized Wigner–Clebsch–Gordan coefficients (generalized WCG coefficients) for
and generalized Wigner–Clebsch–Gordan coefficients (generalized WCG coefficients) for 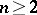 .
.
5) The summation is over all 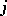 given by:
given by:
 | (a5) |
where 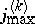 is given by:
is given by:
 | (a6) |
and the minimum value of 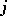 is determined recursively from
is determined recursively from
 | (a7) |
The content of (a1) is completed by giving the explicit form of the unitary irreducible representations entering the direct product. These may be described as follows: Let 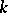 denote an arbitrary non-negative integer and let the pairs
denote an arbitrary non-negative integer and let the pairs 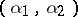 and
and 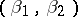 consist of non-negative integers such that
consist of non-negative integers such that 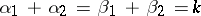 (such pairs are called weights, or contents, of
(such pairs are called weights, or contents, of 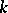 ). Introduce the homogeneous polynomials of degree
). Introduce the homogeneous polynomials of degree 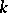 in the elements of an arbitrary
in the elements of an arbitrary 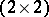 -matrix of indeterminates
-matrix of indeterminates 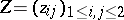 defined by:
defined by:
 | (a8) |
where the summation is to be carried out over all 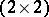 -matrices
-matrices 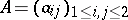 of non-negative integers with row and column sums given by the weights
of non-negative integers with row and column sums given by the weights 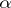 and
and 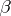 of
of 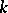 :
:
 | (a9) |
Significant properties of the functions (a8) are:
transposition:
 | (a10) |
where 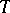 denotes matrix transposition;
denotes matrix transposition;
multiplication:
 | (a11) |
generation:
 | (a12) |
orthogonality:
 | (a13) |
inner product:
 | (a14) |
where the bar denotes complex conjugation, 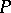 and
and 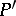 are arbitrary polynomials in the
are arbitrary polynomials in the 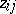 , and
, and
In the first two of these properties, 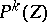 denotes the
denotes the 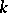 -dimensional matrix with rows and columns enumerated, respectively, by the weights
-dimensional matrix with rows and columns enumerated, respectively, by the weights 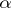 and
and 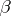 as they assume all possible values for the given
as they assume all possible values for the given 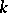 .
.
The unitary irreducible representation functions in (a1) are given in terms of the polynomials 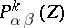 by
by
 | (a15) |
that is, by choosing 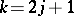 ,
,  ,
, 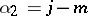 ,
,  ,
, 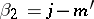 , so that
, so that 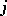 is any integer or half odd integer, and for each such
is any integer or half odd integer, and for each such 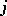 the so-called projection quantum numbers
the so-called projection quantum numbers 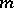 and
and 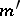 , which are
, which are 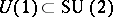 subgroup irreducible representation labels, assume the values
subgroup irreducible representation labels, assume the values 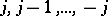 . By convention, these values of
. By convention, these values of 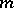 and
and 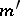 label the rows and columns of the
label the rows and columns of the 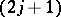 -dimensional unitary matrix
-dimensional unitary matrix 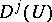 . (Conventionally, the rows are labelled from top to bottom by the greatest to the least value of
. (Conventionally, the rows are labelled from top to bottom by the greatest to the least value of 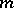 , and the columns are similarly labelled from left to right by
, and the columns are similarly labelled from left to right by 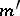 ).
).
Often, the irreducible representation functions (a15) are presented in a form in which 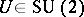 is parametrized. A general way of doing this is to use the property that the
is parametrized. A general way of doing this is to use the property that the 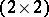 unitary modular matrices are in one-to-one correspondence with the points on the
unitary modular matrices are in one-to-one correspondence with the points on the  -dimensional unit sphere
-dimensional unit sphere 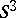 :
:
 | (a16) |
One can then parametrize the points  in any manner one chooses to obtain corresponding parametrizations of the representation functions.
in any manner one chooses to obtain corresponding parametrizations of the representation functions.
The definitions and results given above are the basis relations underlying the origin of all 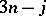 coefficients for all
coefficients for all 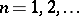 . The general problem leads to beautiful results and unsolved problems involving labelled binary trees, Cayley trivalent trees, and cubic graphs. This subject cannot be developed here, but its flavour can be indicated by the special results for
. The general problem leads to beautiful results and unsolved problems involving labelled binary trees, Cayley trivalent trees, and cubic graphs. This subject cannot be developed here, but its flavour can be indicated by the special results for 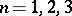 , which are presented in summary form below, focussing on these combinatorial aspects. The formulation of the
, which are presented in summary form below, focussing on these combinatorial aspects. The formulation of the 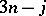 problem can also be given in a purely Lie algebra setting, where the general procedure is known as addition of
problem can also be given in a purely Lie algebra setting, where the general procedure is known as addition of 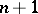 angular momenta.
angular momenta.
There is an extensive literature on this subject. Classical references include [a1], [a25], [a26], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10], [a11], [a12], [a13], [a14], [a15], [a16], [a17], [a18], with more recent work in [a19], [a20], [a21], [a22], [a23], [a24]. The notations in [a19], [a20] are followed.
Vector space constructions.
On assumes as given a vector space 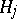 with an inner product, denoted by
with an inner product, denoted by 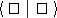 , where
, where 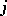 is an arbitrary integer or half integer,
is an arbitrary integer or half integer, 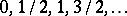 . This vector space
. This vector space 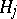 also has an orthonormal basis given by the abstract ket vectors
also has an orthonormal basis given by the abstract ket vectors
 | (a17) |
with an inner product
 | (a18) |
Spaces corresponding to distinct 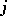 are also to be perpendicular. Finally, there is an action
are also to be perpendicular. Finally, there is an action  , for each
, for each 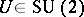 , of the unitary group
, of the unitary group 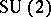 , defined on
, defined on 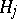 such that the action on the orthonormal basis
such that the action on the orthonormal basis 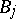 is given by:
is given by:
 | (a19) |
It is the tensor product space  with orthonormal basis
with orthonormal basis
 | (a20) |
that underlies the 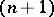 -fold Kronecker product in the left-hand side of (a1). The action of
-fold Kronecker product in the left-hand side of (a1). The action of 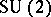 on the space
on the space 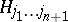 is defined by its action on the basis (a17):
is defined by its action on the basis (a17):
 | (a21) |
Concrete realizations of these spaces are provided by the vectors defined by (a8) and (a15) with inner product (a14):
 | (a22) |
which under left and right translations transform, in consequence of properties (a10) and (a11), as:
 | (a23) |
 | (a24) |
 coefficients.
coefficients.
Relation to Kronecker product.
 | (a25) |
where the 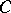 -coefficient is a WCG coefficient, which is an element of the real orthogonal matrix
-coefficient is a WCG coefficient, which is an element of the real orthogonal matrix 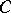 of dimension
of dimension 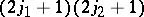 . The coefficient has the properties
. The coefficient has the properties
 | (a26) |
unless 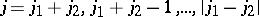 ;
; 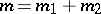 . These WCG coefficients satisfy the orthogonality relations
. These WCG coefficients satisfy the orthogonality relations
rows:
 | (a27) |
columns:
 | (a28) |
Vector space properties.
Relation (a25) is valid when 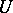 is replaced by
is replaced by 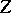 . Using the inner product (a14) gives:
. Using the inner product (a14) gives:
 | (a29) |
This relation (with a sign convention) may be used to calculate the WCG coefficients explicitly. One of the principal uses of the WCG coefficients in physical applications is the construction of a basis of the tensor product space 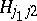 that transforms irreducibly under the action of
that transforms irreducibly under the action of 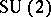 :
:

 | (a30) |
 | (a31) |


A binary tree type of notation has been used to indicate the angular momentum coupling scheme.
Generating function.
J. Schwinger [a2] and T. Regge [a11] discovered the generating function for the WCG coefficients to be the power of a 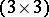 -determinant:
-determinant:
 | (a32) |
where the summation is carried out over all 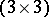 magic square arrays
magic square arrays 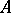 having row and column sums
having row and column sums 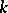 . The coefficient
. The coefficient 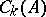 is the restricted multinomial coefficient, given by
is the restricted multinomial coefficient, given by
 | (a33) |
where the summation is to be carried out over all 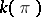 ,
, 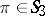 , such that the restriction
, such that the restriction 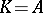 is met:
is met:
 | (a34) |
Because of the restriction in the summation in (a33), the summation can be reduced (asymmetrically) to a sum with only one index.
The WCG coefficient is given by:
 | (a35) |
Symmetries.
It follows directly from the generating function that the 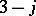 coefficient, which is defined by
coefficient, which is defined by
 | (a36) |
has the 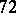 determinantal symmetries associated with row interchange, column interchange, and transposition of the
determinantal symmetries associated with row interchange, column interchange, and transposition of the 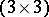 -determinant of
-determinant of 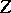 between the parentheses, which transfer directly to the array
between the parentheses, which transfer directly to the array 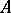 . The
. The 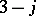 coefficient is either invariant or changes its sign under the transformations of the
coefficient is either invariant or changes its sign under the transformations of the 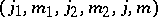 induced by the following transformations of the array
induced by the following transformations of the array  : invariance under even permutations of the rows or columns of
: invariance under even permutations of the rows or columns of 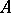 , and under transposition: multiplication by
, and under transposition: multiplication by 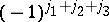 under odd permutations of the rows or columns.
under odd permutations of the rows or columns.
Binary coupling theory.
In the physics literature, the phrase "binary coupling theory" addresses the problem of reducing the multiple Kronecker product (a1) by repeatedly using the reduction result (a25) for two angular momenta. One encounters immediately the problem of how to associate pairs in multiple Kronecker products. For example, for 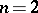 , there are two such associations:
, there are two such associations:
 | (a37) |
For 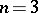 , there are five such associations:
, there are five such associations:
 | (a38) |
In addition, all permutations of the irreducible representation labels  must be considered. Entire textbooks ([a14], [a17], [a22]) have been devoted to this subject, which leads to the representation of
must be considered. Entire textbooks ([a14], [a17], [a22]) have been devoted to this subject, which leads to the representation of 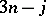 coefficients by pairs of labelled binary trees and cubic graphs ([a20], p. 435). Some limited aspects of this subject are presented here in the context of the
coefficients by pairs of labelled binary trees and cubic graphs ([a20], p. 435). Some limited aspects of this subject are presented here in the context of the 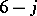 and
and 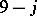 coefficients.
coefficients.
An important topic, but one that is only partially developed, is that of generating functions for the 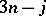 coefficients. The property of a
coefficients. The property of a 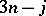 coefficient that characterizes its presentation in terms of a pair of labelled binary trees or in terms of a cubic graph is the set of angular momentum triangles associated with it. This number is always
coefficient that characterizes its presentation in terms of a pair of labelled binary trees or in terms of a cubic graph is the set of angular momentum triangles associated with it. This number is always 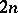 , the number of vertices in the associated cubic graph. A key concept for the generating function of a
, the number of vertices in the associated cubic graph. A key concept for the generating function of a 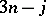 coefficient is that of a triangle monomial. These monomials are defined as follows: Let
coefficient is that of a triangle monomial. These monomials are defined as follows: Let 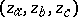 denote three distinct indeterminates and
denote three distinct indeterminates and 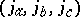 three angular momentum quantum numbers constituting a triangle. The triangle monomial associated with these symbols is defined by
three angular momentum quantum numbers constituting a triangle. The triangle monomial associated with these symbols is defined by
 | (a39) |
Let 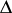 denote the set of triangles associated with a given
denote the set of triangles associated with a given 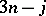 coefficient. The triangle monomial for this
coefficient. The triangle monomial for this 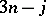 coefficient is defined as
coefficient is defined as
 | (a40) |
The indeterminates 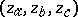 are coordinates associated with each of the
are coordinates associated with each of the 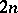 points of the cubic graph corresponding to the
points of the cubic graph corresponding to the 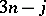 coefficient. This is illustrated concretely below for the
coefficient. This is illustrated concretely below for the 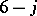 and
and 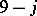 coefficients.
coefficients.
It must be pointed out that  coefficients for
coefficients for 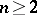 are qualitatively different objects than
are qualitatively different objects than 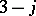 coefficients. The vector space
coefficients. The vector space 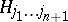 with basis (a20) is the carrier space of the reducible representation of
with basis (a20) is the carrier space of the reducible representation of 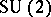 given by the
given by the 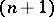 -fold Kronecker product in (a1). This space, which is of dimension
-fold Kronecker product in (a1). This space, which is of dimension
 | (a41) |
may be written as a direct sum of 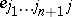 perpendicular vector subspaces:
perpendicular vector subspaces:
 | (a42) |
Each subspace 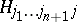 is of dimension
is of dimension 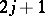 and has a basis of the form (a17) that transforms under the action of
and has a basis of the form (a17) that transforms under the action of 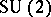 in the standard way given by (a19). The
in the standard way given by (a19). The 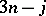 coefficients (
coefficients (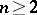 ) are elements of real orthogonal matrices that transform between certain pairs of these subspaces that arise in binary coupling theory, and these coefficients, taken collectively, provide the transformation between all such pairs of subspaces. The
) are elements of real orthogonal matrices that transform between certain pairs of these subspaces that arise in binary coupling theory, and these coefficients, taken collectively, provide the transformation between all such pairs of subspaces. The 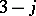 coefficients provide a single such space, as a first step in the construction of the pairs in the binary coupling method.
coefficients provide a single such space, as a first step in the construction of the pairs in the binary coupling method.
One of the consequences of this qualitative difference is that no generating function for a 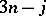 coefficient (
coefficient (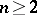 ) is a power of a determinant. It is known for the
) is a power of a determinant. It is known for the 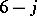 and
and 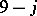 coefficients ([a2], [a15], [a16], [a21]) that these coefficients have generating functions that can be presented in the following uniform manner [a22]: There exists a polynomial
coefficients ([a2], [a15], [a16], [a21]) that these coefficients have generating functions that can be presented in the following uniform manner [a22]: There exists a polynomial  with integer coefficients associated with the cubic graph corresponding to a
with integer coefficients associated with the cubic graph corresponding to a 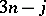 coefficient such that
coefficient such that
 | (a43) |
 | (a44) |
where the symbol 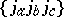 denotes the so-called triangle coefficient, defined by
denotes the so-called triangle coefficient, defined by
 | (a45) |
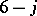 coefficients.
coefficients.
Relation to the Kronecker product.
The coefficients defined by
 | (a46) |
are elements of the orthogonal matrix 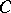 for
for 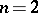 in (a1) that completely reduces the Kronecker product in the first coupling scheme given in (a37).
in (a1) that completely reduces the Kronecker product in the first coupling scheme given in (a37).
Vector space interpretation.

 | (a47) |

 | (a48) |
where the 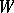 coefficient is called a Racah coefficient. In fact, one could take (a48) as the definition of the Racah coefficient. It is independent of the
coefficient is called a Racah coefficient. In fact, one could take (a48) as the definition of the Racah coefficient. It is independent of the  quantum number; that is, it is a
quantum number; that is, it is a 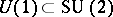 invariant. All other non-trivial binary couplings of three angular momenta lead again to Racah coefficients, up to sign. For
invariant. All other non-trivial binary couplings of three angular momenta lead again to Racah coefficients, up to sign. For 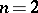 there is only one invariant, the Racah coefficient.
there is only one invariant, the Racah coefficient.
It was a great feat of G. Racah [a25], [a26] (see also [a9], p. 162) to reduce the summation over four WCG coefficients in (a48), each of which is itself a summation over multinomial coefficients, to an expression involving but a single summation index. In the Wigner 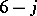 notation, Racah's result is given by:
notation, Racah's result is given by:
 | (a49) |
The triangles in the 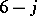 (Racah) coefficient are
(Racah) coefficient are 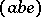 ,
, 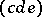 ,
,  ,
, 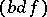 , as inherited from the WCG coefficients in (a48), and
, as inherited from the WCG coefficients in (a48), and 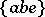 ,
, 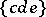 ,
,  ,
, 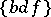 denote the triangle coefficients defined in (a45). The quantities
denote the triangle coefficients defined in (a45). The quantities 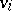 and
and 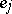 are the discrete vertex and edge functions associated with the tetrahedron:
are the discrete vertex and edge functions associated with the tetrahedron:
 | (a50) |
See (a55), in which the following identifications are to be made:
 | (a51) |
The 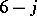 coefficient (now using
coefficient (now using 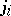 labels throughout) labelled as
labels throughout) labelled as
 | (a52) |
has four triangles, which are conveniently presented as the columns of a 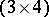 -array:
-array:
 | (a53) |
Generating function.
For the description of the generating function, the real coordinates
 | (a54) |
are introduced, and these are displayed, analogously to (a53) in a 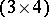 -array, the columns of which are interpreted as the vertices, in Cartesian
-array, the columns of which are interpreted as the vertices, in Cartesian  -dimensional space
-dimensional space 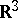 , of a tetrahedron:
, of a tetrahedron:
 | (a55) |

The array of triangles 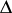 in (a53) is obtained from the
in (a53) is obtained from the 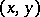 by setting
by setting  .
.
The generating function of the 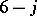 coefficients is now obtained from the labelled tetrahedron in (a55) by the following rules. The function
coefficients is now obtained from the labelled tetrahedron in (a55) by the following rules. The function 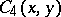 on the left-hand side of (a43) is given as follows. Interchange the
on the left-hand side of (a43) is given as follows. Interchange the  and
and 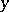 symbols. Then form
symbols. Then form
the vertex function:
the edge function:
 | (a56) |
the tetrahedral function:
Using the tetrahedral function 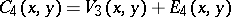 in the general form (a43) for
in the general form (a43) for 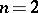 gives the
gives the 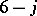 with the labels (a52), where the variables in a given triangle monomial (a40) with exponents given by the columns of
with the labels (a52), where the variables in a given triangle monomial (a40) with exponents given by the columns of 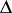 in (a53) are those in the corresponding columns of the array
in (a53) are those in the corresponding columns of the array 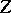 on the left hand side of (a55).
on the left hand side of (a55).
Symmetries.
The symmetries of the 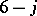 coefficients may be verified directly from the explicit form (a49), or from the generating function. For the coefficient written in the form
coefficients may be verified directly from the explicit form (a49), or from the generating function. For the coefficient written in the form
 | (a57) |
the symmetries are best expressed in terms of the Bargmann 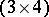 -array
-array
 | (a58) |
as follows: The coefficient (a57) is invariant under all transformations of 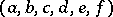 induced by row or column permutations of the Bargmann array. This gives
induced by row or column permutations of the Bargmann array. This gives 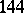 symmetry relations, some simple substitutions, and other simple linear transformations.
symmetry relations, some simple substitutions, and other simple linear transformations.
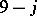 coefficients.
coefficients.
Relation to the Kronecker product.
The coefficients defined by
 | (a59) |
are the elements of the orthogonal matrix 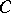 for
for 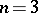 in (a1) that completely reduces the Kronecker product in the bottom binary coupling scheme given in (a38).
in (a1) that completely reduces the Kronecker product in the bottom binary coupling scheme given in (a38).
Vector space interpretation.

 | (a60) |

 | (a61) |
The bracket object is Wigner's notation for the 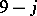 coefficient, and this relation (a61) may be taken as its definition. The summation over six WCG coefficients coming from the inner product in (a61), using (a60), may be reduced to the following summation over
coefficient, and this relation (a61) may be taken as its definition. The summation over six WCG coefficients coming from the inner product in (a61), using (a60), may be reduced to the following summation over 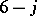 coefficients (a switch to a
coefficients (a switch to a 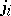 notation has been made):
notation has been made):
 | (a62) |
The six triangles in a 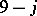 coefficient are inherited from its expression in terms of WCG coefficients, or, equivalently, from the triangles in the
coefficient are inherited from its expression in terms of WCG coefficients, or, equivalently, from the triangles in the 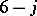 coefficients in (a62) not involving the summation index. It is convenient to display these six triangles as the columns in a
coefficients in (a62) not involving the summation index. It is convenient to display these six triangles as the columns in a 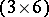 -array:
-array:
 | (a63) |
Generating function.
For the description of the generating function, the real coordinates
 | (a64) |
are introduced, and these are displayed, analogously to (a63), in a 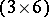 -array, the columns of which are interpreted as the vertices, in Cartesian
-array, the columns of which are interpreted as the vertices, in Cartesian  -dimensional space,
-dimensional space, 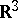 , of a cubic graph on six vertices:
, of a cubic graph on six vertices:
 | (a65) |

The array of triangles 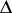 in (a63) is obtained from the
in (a63) is obtained from the 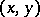 in
in 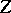 by setting
by setting  . The generating function of the
. The generating function of the 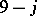 coefficients is now obtained from the labelled cubic graph by the following rules. The function
coefficients is now obtained from the labelled cubic graph by the following rules. The function 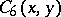 in the left hand side of (a43) is obtained as follows. Interchange the
in the left hand side of (a43) is obtained as follows. Interchange the  and
and 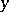 symbols. Then form
symbols. Then form
the vertex function:
 | (a66) |
the edge function:
 | (a67) |
the six point cubic graph function:
 | (a68) |
Using the function  in the general form (a43) for
in the general form (a43) for 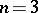 gives the
gives the 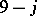 coefficient with the labels (a62), where the variables in a given triangle monomial (a40) with exponents given by the columns of
coefficient with the labels (a62), where the variables in a given triangle monomial (a40) with exponents given by the columns of 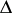 in (a63) are those in the corresponding columns of the array
in (a63) are those in the corresponding columns of the array 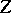 on the left hand side of (a65).
on the left hand side of (a65).
Symmetries.
The 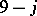 coefficient has
coefficient has 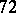 (known) symmetries, and these are just those originating from the
(known) symmetries, and these are just those originating from the 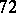 symmetries of the six
symmetries of the six 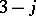 coefficients implicit on the left hand side of (a61). In terms of the coefficient written in the form (a62), these symmetries are expressed by: The
coefficients implicit on the left hand side of (a61). In terms of the coefficient written in the form (a62), these symmetries are expressed by: The 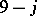 coefficient (a62) is invariant under even permutations of its rows or columns, under transposition of the array, and is multiplied by the factor
coefficient (a62) is invariant under even permutations of its rows or columns, under transposition of the array, and is multiplied by the factor  under odd permutations of its rows or columns.
under odd permutations of its rows or columns.
A great deal of work has been done on the relationship between cubic graphs and 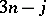 coefficients, and the results can not even be surveyed here. It is important to point out, however, that for
coefficients, and the results can not even be surveyed here. It is important to point out, however, that for 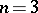 there is a second non-isomorphic cubic graph on six vertices, the prism, or wedge, which leads to a simple product (with dimensional factors) of two
there is a second non-isomorphic cubic graph on six vertices, the prism, or wedge, which leads to a simple product (with dimensional factors) of two 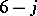 coefficients. While this is important for transforming between the relevant coupling schemes, it does not lead to a new
coefficients. While this is important for transforming between the relevant coupling schemes, it does not lead to a new  coefficient. Indeed, it can be proved that every
coefficient. Indeed, it can be proved that every 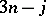 coefficient is a sum over products of
coefficient is a sum over products of 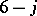 coefficients, and sometimes this sum may degenerate to a product of
coefficients, and sometimes this sum may degenerate to a product of 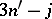 coefficients (
coefficients (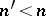 ), in which case it is not counted as new. For
), in which case it is not counted as new. For 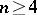 there are always fewer "new"
there are always fewer "new" 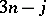 coefficients than non-isomorphic cubic graphs. The general problem of the relation between
coefficients than non-isomorphic cubic graphs. The general problem of the relation between 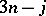 coefficients and non-isomorphic cubic graphs of
coefficients and non-isomorphic cubic graphs of 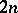 vertices is unsolved.
vertices is unsolved.
Relevant to the classification of 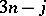 coefficients, indeed, for the definition of what the term "classification" means, are three basic relations:
coefficients, indeed, for the definition of what the term "classification" means, are three basic relations:
triangle transformation:
 | (a69) |
Racah sum rule:
 | (a70) |
Biedenharn–Elliot identity, [a4], [a5]:
 | (a71) |
Each of these relations has an interpretation in terms of fundamental operations in mathematics: The triangle transformation rule is a consequence of the associativity of three symplecton polynomials, which are polynomials of the form 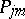 over the four non-commuting variables
over the four non-commuting variables  (or, equivalently, over two bosons and their conjugates) which transform irreducibly under a well-defined commutation action of
(or, equivalently, over two bosons and their conjugates) which transform irreducibly under a well-defined commutation action of 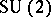 . Racah's sum rule has an interpretation in terms of the commutativity of a diagram associated with the coupling of three angular momenta. The Biedenharn–Elliot identity is a consequence of the associative law for three unit tensor operators. For a discussion of each of these results, see [a20], pp. 243; 453; 30.
. Racah's sum rule has an interpretation in terms of the commutativity of a diagram associated with the coupling of three angular momenta. The Biedenharn–Elliot identity is a consequence of the associative law for three unit tensor operators. For a discussion of each of these results, see [a20], pp. 243; 453; 30.
References
| [a1] | E.P. Wigner, "On the matrices which reduce the Kronecker products of representation of S.R. groups" L.C. Biedenharn (ed.) H. van Dam (ed.) , Quantum Theory of Angular Momentum , Acad. Press (1965) pp. 87–133 (Original: 1940 (unpublished)) |
| [a2] | J. Schwinger, "On angular momentum" L.C. Bidenharn (ed.) H. van Dam (ed.) , Quantum Theory of Angular Momentum , Acad. Press (1965) pp. 229–279 (Original: U.S. Atomic Energy Commission Reports NYO–3071, 1952 (unpublished)) |
| [a3] | L.C. Biedenharn, J.M. Blatt, M.E. Rose, "Some properties of the Racah and associated coefficients" Rev. Mod. Phys. , 24 (1952) pp. 249–257 |
| [a4] | L.C. Biedenharn, "An identity satisfied by Racah coefficients" J. Math. Phys. , 31 (1953) pp. 287–293 |
| [a5] | J.P. Elliot, "Theoretical studies in nuclear spectroscopy. V: The matrix elements of non-central forces with an application to the  -shell" Proc. Roy. Soc. A , 218 (1953) pp. 345–370 -shell" Proc. Roy. Soc. A , 218 (1953) pp. 345–370 |
| [a6] | H.A. Jahn, J. Hope, "Symmetry properties of the Wigner 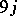 symbol" Phys. Rev. , 93 (1954) pp. 318–321 symbol" Phys. Rev. , 93 (1954) pp. 318–321 |
| [a7] | A. Arima, H. Horie, Y. Tanabe, "Generalized Racah coefficient and its application" Progress Theor. Phys. (Kyoto) , 11 (1954) pp. 143–154 |
| [a8] | A.R. Edmonds, "Angular momentum in quantum mechanics" , Princeton Univ. Press (1957) |
| [a9] | M.E. Rose, "Elementary theory of angular momentum" , Wiley (1957) |
| [a10] | U. Fano, G. Racah, "Irreducible tensorial sets" , Acad. Press (1959) |
| [a11] | T. Regge, "Symmetry properties of Clebsch–Gordan coefficients" Nuovo Cim. , 10 (1958) pp. 544–545 |
| [a12] | T. Regge, "Symmetry properties of Racah's coefficients" Nuovo Cim. , 11 (1959) pp. 116–117 |
| [a13] | W.T. Sharp, "Racah algebra and the contraction of groups" , Thesis Princeton Univ. Press (1960) |
| [a14] | A.P. Yutsis (Jucys), I.B. Levinson, V.V. Vanagas, "Mathematical apparatus of the theory of angular momentum" , Gordon&Breach (1964) (In Russian) |
| [a15] | V. Bargmann, "On the representations of the rotation group" Rev. Mod. Phys. , 345 (1962) pp. 829–845 |
| [a16] | A.C.T. Wu, "Structure of the Wigner 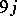 coefficients in the Bargmann approach" J. Math. Phys. , 13 (1972) pp. 84–90 coefficients in the Bargmann approach" J. Math. Phys. , 13 (1972) pp. 84–90 |
| [a17] | D.A. Varshalovich, A.N. Moskalev, V.K. Khersonskii, "Quantum theory of angular momentum" , Nauka (1975) (In Russian) |
| [a18] | A.P. Yutsis (Jucys), A.A. Bandzaitis, "Angular momentum theory in quantum mechanics" , Molslas , Vilnius (1977) (In Russian) |
| [a19] | L.C. Biedenharn, J.D. Louck, "Angular momentum in quantum physics" , Encycl. Math. Sci. , 8 , Cambridge Univ. Press (1981) |
| [a20] | L.C. Biedenharn, J.D. Louck, "The Racah–Wigner algebra in quantum theory" , Encycl. Math. Sci. , 9 , Cambridge Univ. Press (1981) |
| [a21] | B.R. Judd, G.M.S. Lister, "A class of generalized 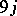 coefficients for coefficients for 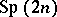 " J. Phys. A: Math. Gen. , 20 (1986) pp. 3159–3169 " J. Phys. A: Math. Gen. , 20 (1986) pp. 3159–3169 |
| [a22] | L.C. Biedenharn, W.Y.C. Chen, M.A. Lohe, J.D. Louck, "The role of 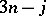 coefficients in coefficients in 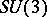 " T. Lulek (ed.) W. Florek (ed.) S. Walcerz (ed.) , Proc. 3rd SSCPM , World Sci. (1995) pp. 150–182 " T. Lulek (ed.) W. Florek (ed.) S. Walcerz (ed.) , Proc. 3rd SSCPM , World Sci. (1995) pp. 150–182 |
| [a23] | M. Danos, "??" , ?? (199?) |
| [a24] | J.D. Louck, "Unitary symmetry, combinatorics and generating functions" J. Discrete Math. , ?? (199?) |
| [a25] | G. Racah, "Theory of complex spectra. II" Phys. Rev. , 62 (1942) pp. 438–462 |
| [a26] | G. Racah, "Theory of complex spectra. III" Phys. Rev. , 63 (1943) pp. 367–382 |
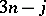 coefficients enter mathematics and physics in describing the reduction of the
coefficients enter mathematics and physics in describing the reduction of the 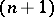 -fold Kronecker product of the unitary irreducible representations of the unitary unimodular group
-fold Kronecker product of the unitary irreducible representations of the unitary unimodular group 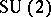 , the group of
, the group of 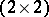 unitary unimodular matrices, into unitary irreducible representations of
unitary unimodular matrices, into unitary irreducible representations of 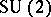 . This reduction has the form:
. This reduction has the form:

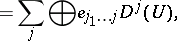
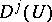 denotes the
denotes the 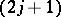 -dimensional unitary irreducible representation of
-dimensional unitary irreducible representation of 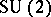 given explicitly below, where
given explicitly below, where  , and this label is called an irreducible representation label or an angular momentum quantum number.
, and this label is called an irreducible representation label or an angular momentum quantum number.
 denotes the matrix direct product (Kronecker product), and
denotes the matrix direct product (Kronecker product), and 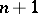 such products enter the left-hand side with arbitrary irreducible representation labels
such products enter the left-hand side with arbitrary irreducible representation labels 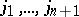 .
.
 denotes the matrix direct sum, and the direct sum on the right-hand side contains each irreducible representation
denotes the matrix direct sum, and the direct sum on the right-hand side contains each irreducible representation 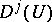 a number of times equal to
a number of times equal to

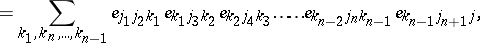
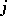 is any irreducible representation label given by
is any irreducible representation label given by

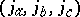 of irreducible representation labels, the quantity
of irreducible representation labels, the quantity 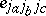 is
is  or
or 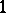 , and it is
, and it is 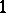 if and only if the so-called triangle conditions are satisfied:
if and only if the so-called triangle conditions are satisfied:

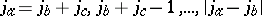 .
.
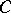 denotes a real orthogonal matrix of dimension
denotes a real orthogonal matrix of dimension 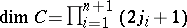 , with elements called Wigner–Clebsch–Gordan coefficients (WCG coefficients) for
, with elements called Wigner–Clebsch–Gordan coefficients (WCG coefficients) for 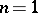 and generalized Wigner–Clebsch–Gordan coefficients (generalized WCG coefficients) for
and generalized Wigner–Clebsch–Gordan coefficients (generalized WCG coefficients) for 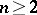 .
.
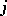 given by:
given by:

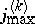 is given by:
is given by:

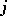 is determined recursively from
is determined recursively from

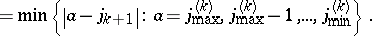
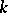 denote an arbitrary non-negative integer and let the pairs
denote an arbitrary non-negative integer and let the pairs 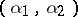 and
and 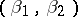 consist of non-negative integers such that
consist of non-negative integers such that 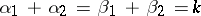 (such pairs are called weights, or contents, of
(such pairs are called weights, or contents, of 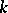 ). Introduce the homogeneous polynomials of degree
). Introduce the homogeneous polynomials of degree 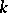 in the elements of an arbitrary
in the elements of an arbitrary 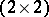 -matrix of indeterminates
-matrix of indeterminates 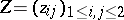 defined by:
defined by:

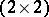 -matrices
-matrices 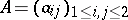 of non-negative integers with row and column sums given by the weights
of non-negative integers with row and column sums given by the weights 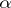 and
and 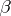 of
of 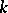 :
:


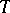 denotes matrix transposition;
denotes matrix transposition;




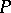 and
and 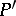 are arbitrary polynomials in the
are arbitrary polynomials in the 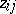 , and
, and
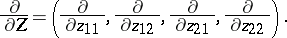
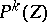 denotes the
denotes the 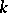 -dimensional matrix with rows and columns enumerated, respectively, by the weights
-dimensional matrix with rows and columns enumerated, respectively, by the weights 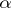 and
and 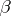 as they assume all possible values for the given
as they assume all possible values for the given 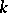 .
.
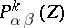 by
by

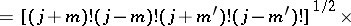

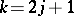 ,
,  ,
, 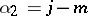 ,
,  ,
, 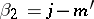 , so that
, so that 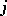 is any integer or half odd integer, and for each such
is any integer or half odd integer, and for each such 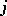 the so-called projection quantum numbers
the so-called projection quantum numbers 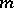 and
and 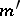 , which are
, which are 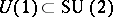 subgroup irreducible representation labels, assume the values
subgroup irreducible representation labels, assume the values 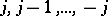 . By convention, these values of
. By convention, these values of 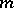 and
and 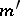 label the rows and columns of the
label the rows and columns of the 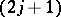 -dimensional unitary matrix
-dimensional unitary matrix 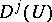 . (Conventionally, the rows are labelled from top to bottom by the greatest to the least value of
. (Conventionally, the rows are labelled from top to bottom by the greatest to the least value of 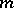 , and the columns are similarly labelled from left to right by
, and the columns are similarly labelled from left to right by 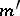 ).
).
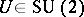 is parametrized. A general way of doing this is to use the property that the
is parametrized. A general way of doing this is to use the property that the 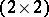 unitary modular matrices are in one-to-one correspondence with the points on the
unitary modular matrices are in one-to-one correspondence with the points on the  -dimensional unit sphere
-dimensional unit sphere 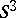 :
:

 in any manner one chooses to obtain corresponding parametrizations of the representation functions.
in any manner one chooses to obtain corresponding parametrizations of the representation functions.
 coefficients for all
coefficients for all 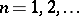 . The general problem leads to beautiful results and unsolved problems involving labelled binary trees, Cayley trivalent trees, and cubic graphs. This subject cannot be developed here, but its flavour can be indicated by the special results for
. The general problem leads to beautiful results and unsolved problems involving labelled binary trees, Cayley trivalent trees, and cubic graphs. This subject cannot be developed here, but its flavour can be indicated by the special results for 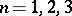 , which are presented in summary form below, focussing on these combinatorial aspects. The formulation of the
, which are presented in summary form below, focussing on these combinatorial aspects. The formulation of the 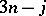 problem can also be given in a purely Lie algebra setting, where the general procedure is known as addition of
problem can also be given in a purely Lie algebra setting, where the general procedure is known as addition of 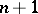 angular momenta.
angular momenta.
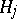 with an inner product, denoted by
with an inner product, denoted by 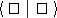 , where
, where 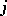 is an arbitrary integer or half integer,
is an arbitrary integer or half integer, 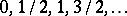 . This vector space
. This vector space 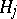 also has an orthonormal basis given by the abstract ket vectors
also has an orthonormal basis given by the abstract ket vectors


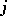 are also to be perpendicular. Finally, there is an action
are also to be perpendicular. Finally, there is an action  , for each
, for each 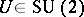 , of the unitary group
, of the unitary group 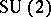 , defined on
, defined on 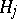 such that the action on the orthonormal basis
such that the action on the orthonormal basis 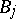 is given by:
is given by:

 with orthonormal basis
with orthonormal basis

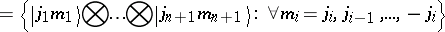
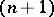 -fold Kronecker product in the left-hand side of (a1). The action of
-fold Kronecker product in the left-hand side of (a1). The action of 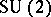 on the space
on the space 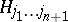 is defined by its action on the basis (a17):
is defined by its action on the basis (a17):
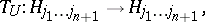

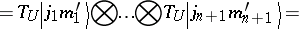
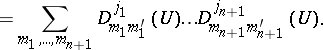
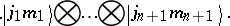



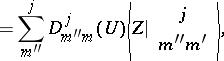


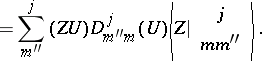
 coefficients.
coefficients.
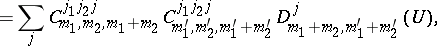
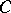 -coefficient is a WCG coefficient, which is an element of the real orthogonal matrix
-coefficient is a WCG coefficient, which is an element of the real orthogonal matrix 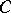 of dimension
of dimension 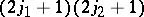 . The coefficient has the properties
. The coefficient has the properties

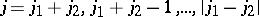 ;
; 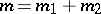 . These WCG coefficients satisfy the orthogonality relations
. These WCG coefficients satisfy the orthogonality relations


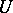 is replaced by
is replaced by 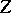 . Using the inner product (a14) gives:
. Using the inner product (a14) gives:

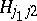 that transforms irreducibly under the action of
that transforms irreducibly under the action of 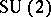 :
:


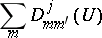
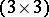 -determinant:
-determinant:

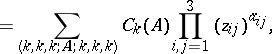
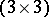 magic square arrays
magic square arrays 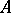 having row and column sums
having row and column sums 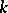 . The coefficient
. The coefficient 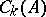 is the restricted multinomial coefficient, given by
is the restricted multinomial coefficient, given by


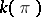 ,
, 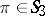 , such that the restriction
, such that the restriction 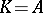 is met:
is met:



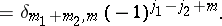
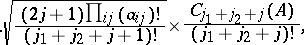
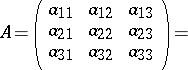

 coefficient, which is defined by
coefficient, which is defined by

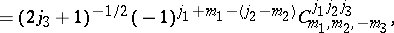
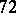 determinantal symmetries associated with row interchange, column interchange, and transposition of the
determinantal symmetries associated with row interchange, column interchange, and transposition of the 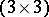 -determinant of
-determinant of 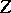 between the parentheses, which transfer directly to the array
between the parentheses, which transfer directly to the array 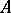 . The
. The 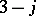 coefficient is either invariant or changes its sign under the transformations of the
coefficient is either invariant or changes its sign under the transformations of the 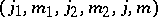 induced by the following transformations of the array
induced by the following transformations of the array  : invariance under even permutations of the rows or columns of
: invariance under even permutations of the rows or columns of 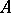 , and under transposition: multiplication by
, and under transposition: multiplication by 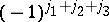 under odd permutations of the rows or columns.
under odd permutations of the rows or columns.
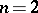 , there are two such associations:
, there are two such associations:

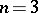 , there are five such associations:
, there are five such associations:

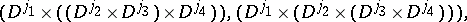
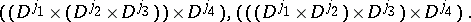
 must be considered. Entire textbooks ([a14], [a17], [a22]) have been devoted to this subject, which leads to the representation of
must be considered. Entire textbooks ([a14], [a17], [a22]) have been devoted to this subject, which leads to the representation of 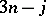 coefficients by pairs of labelled binary trees and cubic graphs ([a20], p. 435). Some limited aspects of this subject are presented here in the context of the
coefficients by pairs of labelled binary trees and cubic graphs ([a20], p. 435). Some limited aspects of this subject are presented here in the context of the 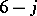 and
and 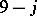 coefficients.
coefficients.
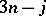 coefficients. The property of a
coefficients. The property of a 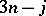 coefficient that characterizes its presentation in terms of a pair of labelled binary trees or in terms of a cubic graph is the set of angular momentum triangles associated with it. This number is always
coefficient that characterizes its presentation in terms of a pair of labelled binary trees or in terms of a cubic graph is the set of angular momentum triangles associated with it. This number is always 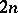 , the number of vertices in the associated cubic graph. A key concept for the generating function of a
, the number of vertices in the associated cubic graph. A key concept for the generating function of a 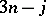 coefficient is that of a triangle monomial. These monomials are defined as follows: Let
coefficient is that of a triangle monomial. These monomials are defined as follows: Let 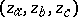 denote three distinct indeterminates and
denote three distinct indeterminates and 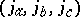 three angular momentum quantum numbers constituting a triangle. The triangle monomial associated with these symbols is defined by
three angular momentum quantum numbers constituting a triangle. The triangle monomial associated with these symbols is defined by

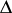 denote the set of triangles associated with a given
denote the set of triangles associated with a given 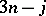 coefficient. The triangle monomial for this
coefficient. The triangle monomial for this 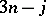 coefficient is defined as
coefficient is defined as

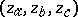 are coordinates associated with each of the
are coordinates associated with each of the 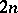 points of the cubic graph corresponding to the
points of the cubic graph corresponding to the 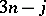 coefficient. This is illustrated concretely below for the
coefficient. This is illustrated concretely below for the 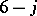 and
and 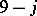 coefficients.
coefficients.
 coefficients for
coefficients for 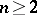 are qualitatively different objects than
are qualitatively different objects than 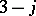 coefficients. The vector space
coefficients. The vector space 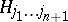 with basis (a20) is the carrier space of the reducible representation of
with basis (a20) is the carrier space of the reducible representation of 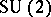 given by the
given by the 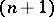 -fold Kronecker product in (a1). This space, which is of dimension
-fold Kronecker product in (a1). This space, which is of dimension

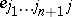 perpendicular vector subspaces:
perpendicular vector subspaces:

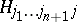 is of dimension
is of dimension 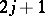 and has a basis of the form (a17) that transforms under the action of
and has a basis of the form (a17) that transforms under the action of 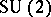 in the standard way given by (a19). The
in the standard way given by (a19). The 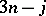 coefficients (
coefficients (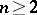 ) are elements of real orthogonal matrices that transform between certain pairs of these subspaces that arise in binary coupling theory, and these coefficients, taken collectively, provide the transformation between all such pairs of subspaces. The
) are elements of real orthogonal matrices that transform between certain pairs of these subspaces that arise in binary coupling theory, and these coefficients, taken collectively, provide the transformation between all such pairs of subspaces. The 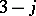 coefficients provide a single such space, as a first step in the construction of the pairs in the binary coupling method.
coefficients provide a single such space, as a first step in the construction of the pairs in the binary coupling method.
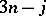 coefficient (
coefficient (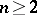 ) is a power of a determinant. It is known for the
) is a power of a determinant. It is known for the 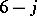 and
and 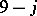 coefficients ([a2], [a15], [a16], [a21]) that these coefficients have generating functions that can be presented in the following uniform manner [a22]: There exists a polynomial
coefficients ([a2], [a15], [a16], [a21]) that these coefficients have generating functions that can be presented in the following uniform manner [a22]: There exists a polynomial  with integer coefficients associated with the cubic graph corresponding to a
with integer coefficients associated with the cubic graph corresponding to a 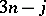 coefficient such that
coefficient such that


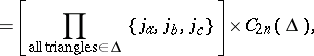
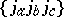 denotes the so-called triangle coefficient, defined by
denotes the so-called triangle coefficient, defined by

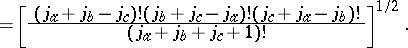
 coefficients.
coefficients.
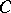 for
for  in (a1) that completely reduces the Kronecker product in the first coupling scheme given in (a37).
in (a1) that completely reduces the Kronecker product in the first coupling scheme given in (a37).



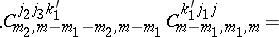
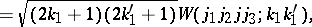
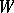 coefficient is called a Racah coefficient. In fact, one could take (a48) as the definition of the Racah coefficient. It is independent of the
coefficient is called a Racah coefficient. In fact, one could take (a48) as the definition of the Racah coefficient. It is independent of the  quantum number; that is, it is a
quantum number; that is, it is a 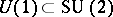 invariant. All other non-trivial binary couplings of three angular momenta lead again to Racah coefficients, up to sign. For
invariant. All other non-trivial binary couplings of three angular momenta lead again to Racah coefficients, up to sign. For 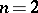 there is only one invariant, the Racah coefficient.
there is only one invariant, the Racah coefficient.
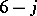 notation, Racah's result is given by:
notation, Racah's result is given by:

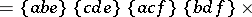
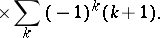
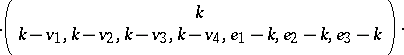
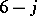 (Racah) coefficient are
(Racah) coefficient are 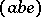 ,
, 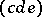 ,
,  ,
, 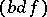 , as inherited from the WCG coefficients in (a48), and
, as inherited from the WCG coefficients in (a48), and 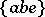 ,
, 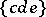 ,
,  ,
, 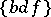 denote the triangle coefficients defined in (a45). The quantities
denote the triangle coefficients defined in (a45). The quantities 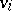 and
and 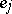 are the discrete vertex and edge functions associated with the tetrahedron:
are the discrete vertex and edge functions associated with the tetrahedron:

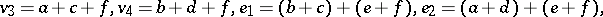
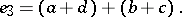



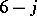 coefficient (now using
coefficient (now using 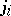 labels throughout) labelled as
labels throughout) labelled as

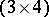 -array:
-array:



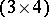 -array, the columns of which are interpreted as the vertices, in Cartesian
-array, the columns of which are interpreted as the vertices, in Cartesian  -dimensional space
-dimensional space 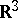 , of a tetrahedron:
, of a tetrahedron:

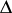 in (a53) is obtained from the
in (a53) is obtained from the 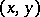 by setting
by setting  .
.
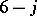 coefficients is now obtained from the labelled tetrahedron in (a55) by the following rules. The function
coefficients is now obtained from the labelled tetrahedron in (a55) by the following rules. The function 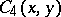 on the left-hand side of (a43) is given as follows. Interchange the
on the left-hand side of (a43) is given as follows. Interchange the  and
and 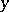 symbols. Then form
symbols. Then form
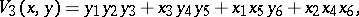

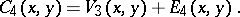
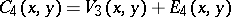 in the general form (a43) for
in the general form (a43) for 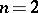 gives the
gives the 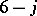 with the labels (a52), where the variables in a given triangle monomial (a40) with exponents given by the columns of
with the labels (a52), where the variables in a given triangle monomial (a40) with exponents given by the columns of 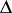 in (a53) are those in the corresponding columns of the array
in (a53) are those in the corresponding columns of the array 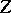 on the left hand side of (a55).
on the left hand side of (a55).
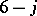 coefficients may be verified directly from the explicit form (a49), or from the generating function. For the coefficient written in the form
coefficients may be verified directly from the explicit form (a49), or from the generating function. For the coefficient written in the form

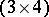 -array
-array

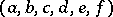 induced by row or column permutations of the Bargmann array. This gives
induced by row or column permutations of the Bargmann array. This gives 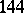 symmetry relations, some simple substitutions, and other simple linear transformations.
symmetry relations, some simple substitutions, and other simple linear transformations.
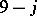 coefficients.
coefficients.
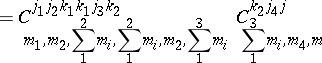
 for
for 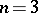 in (a1) that completely reduces the Kronecker product in the bottom binary coupling scheme given in (a38).
in (a1) that completely reduces the Kronecker product in the bottom binary coupling scheme given in (a38).

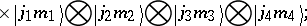

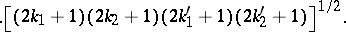
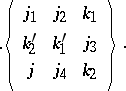
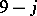 coefficient, and this relation (a61) may be taken as its definition. The summation over six WCG coefficients coming from the inner product in (a61), using (a60), may be reduced to the following summation over
coefficient, and this relation (a61) may be taken as its definition. The summation over six WCG coefficients coming from the inner product in (a61), using (a60), may be reduced to the following summation over 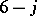 coefficients (a switch to a
coefficients (a switch to a 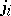 notation has been made):
notation has been made):

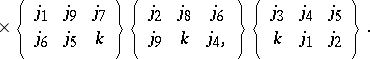
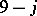 coefficient are inherited from its expression in terms of WCG coefficients, or, equivalently, from the triangles in the
coefficient are inherited from its expression in terms of WCG coefficients, or, equivalently, from the triangles in the 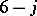 coefficients in (a62) not involving the summation index. It is convenient to display these six triangles as the columns in a
coefficients in (a62) not involving the summation index. It is convenient to display these six triangles as the columns in a 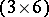 -array:
-array:


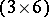 -array, the columns of which are interpreted as the vertices, in Cartesian
-array, the columns of which are interpreted as the vertices, in Cartesian  -dimensional space,
-dimensional space, 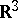 , of a cubic graph on six vertices:
, of a cubic graph on six vertices:

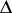 in (a63) is obtained from the
in (a63) is obtained from the 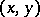 in
in 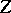 by setting
by setting  . The generating function of the
. The generating function of the 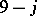 coefficients is now obtained from the labelled cubic graph by the following rules. The function
coefficients is now obtained from the labelled cubic graph by the following rules. The function 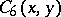 in the left hand side of (a43) is obtained as follows. Interchange the
in the left hand side of (a43) is obtained as follows. Interchange the  and
and 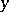 symbols. Then form
symbols. Then form

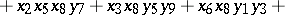
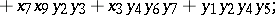


 in the general form (a43) for
in the general form (a43) for 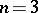 gives the
gives the 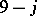 coefficient with the labels (a62), where the variables in a given triangle monomial (a40) with exponents given by the columns of
coefficient with the labels (a62), where the variables in a given triangle monomial (a40) with exponents given by the columns of 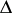 in (a63) are those in the corresponding columns of the array
in (a63) are those in the corresponding columns of the array 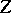 on the left hand side of (a65).
on the left hand side of (a65).
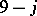 coefficient has
coefficient has 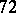 (known) symmetries, and these are just those originating from the
(known) symmetries, and these are just those originating from the 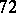 symmetries of the six
symmetries of the six 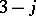 coefficients implicit on the left hand side of (a61). In terms of the coefficient written in the form (a62), these symmetries are expressed by: The
coefficients implicit on the left hand side of (a61). In terms of the coefficient written in the form (a62), these symmetries are expressed by: The 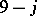 coefficient (a62) is invariant under even permutations of its rows or columns, under transposition of the array, and is multiplied by the factor
coefficient (a62) is invariant under even permutations of its rows or columns, under transposition of the array, and is multiplied by the factor  under odd permutations of its rows or columns.
under odd permutations of its rows or columns.
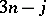 coefficients, and the results can not even be surveyed here. It is important to point out, however, that for
coefficients, and the results can not even be surveyed here. It is important to point out, however, that for 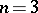 there is a second non-isomorphic cubic graph on six vertices, the prism, or wedge, which leads to a simple product (with dimensional factors) of two
there is a second non-isomorphic cubic graph on six vertices, the prism, or wedge, which leads to a simple product (with dimensional factors) of two 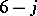 coefficients. While this is important for transforming between the relevant coupling schemes, it does not lead to a new
coefficients. While this is important for transforming between the relevant coupling schemes, it does not lead to a new  coefficient. Indeed, it can be proved that every
coefficient. Indeed, it can be proved that every 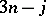 coefficient is a sum over products of
coefficient is a sum over products of 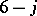 coefficients, and sometimes this sum may degenerate to a product of
coefficients, and sometimes this sum may degenerate to a product of 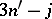 coefficients (
coefficients (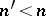 ), in which case it is not counted as new. For
), in which case it is not counted as new. For 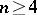 there are always fewer "new"
there are always fewer "new" 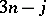 coefficients than non-isomorphic cubic graphs. The general problem of the relation between
coefficients than non-isomorphic cubic graphs. The general problem of the relation between 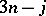 coefficients and non-isomorphic cubic graphs of
coefficients and non-isomorphic cubic graphs of 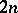 vertices is unsolved.
vertices is unsolved.
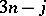 coefficients, indeed, for the definition of what the term "classification" means, are three basic relations:
coefficients, indeed, for the definition of what the term "classification" means, are three basic relations:


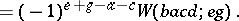


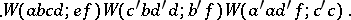
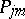 over the four non-commuting variables
over the four non-commuting variables  (or, equivalently, over two bosons and their conjugates) which transform irreducibly under a well-defined commutation action of
(or, equivalently, over two bosons and their conjugates) which transform irreducibly under a well-defined commutation action of 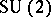 . Racah's sum rule has an interpretation in terms of the commutativity of a diagram associated with the coupling of three angular momenta. The Biedenharn–Elliot identity is a consequence of the associative law for three unit tensor operators. For a discussion of each of these results, see [a20], pp. 243; 453; 30.
. Racah's sum rule has an interpretation in terms of the commutativity of a diagram associated with the coupling of three angular momenta. The Biedenharn–Elliot identity is a consequence of the associative law for three unit tensor operators. For a discussion of each of these results, see [a20], pp. 243; 453; 30.
 -shell" Proc. Roy. Soc. A , 218 (1953) pp. 345–370
-shell" Proc. Roy. Soc. A , 218 (1953) pp. 345–370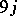 symbol" Phys. Rev. , 93 (1954) pp. 318–321
symbol" Phys. Rev. , 93 (1954) pp. 318–321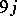 coefficients in the Bargmann approach" J. Math. Phys. , 13 (1972) pp. 84–90
coefficients in the Bargmann approach" J. Math. Phys. , 13 (1972) pp. 84–90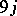 coefficients for
coefficients for 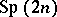 " J. Phys. A: Math. Gen. , 20 (1986) pp. 3159–3169
" J. Phys. A: Math. Gen. , 20 (1986) pp. 3159–3169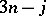 coefficients in
coefficients in 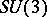 " T. Lulek (ed.) W. Florek (ed.) S. Walcerz (ed.) , Proc. 3rd SSCPM , World Sci. (1995) pp. 150–182
" T. Lulek (ed.) W. Florek (ed.) S. Walcerz (ed.) , Proc. 3rd SSCPM , World Sci. (1995) pp. 150–182