Quotient space
of a dynamical system  given on a topological space
given on a topological space 
The quotient space of  relative to the equivalence:
relative to the equivalence:  if the points
if the points  and
and  belong to the same trajectory. In other words, the points of the quotient space are the trajectories of the dynamical system
belong to the same trajectory. In other words, the points of the quotient space are the trajectories of the dynamical system  (in a different notation
(in a different notation  , see [1]), and the topology is the strongest in which the mapping associating each point of
, see [1]), and the topology is the strongest in which the mapping associating each point of  with its trajectory is continuous (thus,
with its trajectory is continuous (thus,
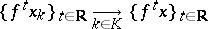 |
( is a directed set) if and only if there are
is a directed set) if and only if there are 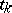 such that
such that
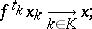 |
if  is a metric space, then
is a metric space, then  ). The quotient spaces of many dynamical systems do not satisfy any of the separation axioms, even if
). The quotient spaces of many dynamical systems do not satisfy any of the separation axioms, even if  does. For example, if
does. For example, if 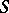 is a minimal set, then the closure of every non-empty set in the quotient space is the whole quotient space. If a dynamical system given on a metric space is completely unstable (see Complete instability), then for its quotient space to be Hausdorff it is necessary and sufficient that this dynamical system does not have saddles at infinity (cf. Saddle at infinity).
is a minimal set, then the closure of every non-empty set in the quotient space is the whole quotient space. If a dynamical system given on a metric space is completely unstable (see Complete instability), then for its quotient space to be Hausdorff it is necessary and sufficient that this dynamical system does not have saddles at infinity (cf. Saddle at infinity).
References
| [1] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [2] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
| [3] | V.M. Millionshchikov, "A comment on the Nemytskii–Bebutov theorem concerning unstable dynamic system" Differential Eq. , 10 : 12 (1975) pp. 1775–1776 Differensial'nye Uravneniya , 10 : 12 (1975) pp. 2292–2293 |
Comments
In general, let  be a topological space and
be a topological space and  an equivalence relation on
an equivalence relation on  (equivalently:
(equivalently:  is the disjoint union of subsets
is the disjoint union of subsets  ,
, 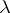 in some index set
in some index set 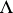 , not necessarily finite; in that case,
, not necessarily finite; in that case,  if and only if
if and only if  and
and  belong to the same
belong to the same  ). The quotient space (also called decomposition space, see Quotient mapping)
). The quotient space (also called decomposition space, see Quotient mapping)  is the space whose points are the
is the space whose points are the  -equivalence classes, endowed with the finest (i.e. strongest) topology making the quotient mapping
-equivalence classes, endowed with the finest (i.e. strongest) topology making the quotient mapping  continuous (here
continuous (here 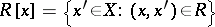 for
for 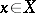 ). The object discussed above, where the equivalence classes are the trajectories of a dynamical system, is usually called the orbit space of the dynamical system. The characterization of convergence of a net (or generalized sequence) in the orbit space cannot be generalized to arbitrary quotient spaces: it is valid because for orbit spaces the quotient mapping is always an open mapping.
). The object discussed above, where the equivalence classes are the trajectories of a dynamical system, is usually called the orbit space of the dynamical system. The characterization of convergence of a net (or generalized sequence) in the orbit space cannot be generalized to arbitrary quotient spaces: it is valid because for orbit spaces the quotient mapping is always an open mapping.
That for a completely-unstable system the orbit space has a Hausdorff topology if and only if the dynamical system has no saddles at infinity is related with the results in [a2]. See also Proposition 14 in [a1].
References
| [a1] | O. Hajek, "Prolongation in topological dynamics" , Sem. Differential Equations and Dynamical Systems II , Lect. notes in math. , 144 , Springer (1970) pp. 79–89 |
| [a2] | L. Markus, "Parallel dynamical systems" Topology , 8 (1969) pp. 47–57 |
| [a3] | R. Engelking, "General topology" , Heldermann (1989) |
Quotient space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quotient_space&oldid=11882