Difference between revisions of "Quantum groups"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) (tex done, commutative diagrams adjusted (could be further optimized...)) |
||
| Line 1: | Line 1: | ||
| − | The phrase "quantum group" is more or less a synonym for "Hopf algebra" . More precisely, the category of quantum groups is defined in [[#References|[a1]]] to be dual to the category of Hopf algebras. This is natural for the following reason. There is the following general principle: The functor | + | {{TEX|done}} |
| + | The phrase "quantum group" is more or less a synonym for "Hopf algebra" . More precisely, the category of quantum groups is defined in [[#References|[a1]]] to be dual to the category of Hopf algebras. This is natural for the following reason. There is the following general principle: The functor $ X \mapsto \{ \textrm{ the algebra of functions on } X \} $ | ||
| + | is an anti-equivalence between the category of "spaces" and the category of commutative associative unital algebras, perhaps with some additional structures or properties (this principle becomes a theorem if "space" is understood to be "affine scheme" or "compact topological space" , and "algebra" is understood to mean "C*-algebra" ). So one can translate the definition of a group into the language of algebras: instead of a space $ G $ | ||
| + | with an associative operation $ G \times G \rightarrow G $ | ||
| + | one obtains a commutative algebra $ A $ | ||
| + | over a commutative ring $ k $ | ||
| + | with a homomorphism $ \Delta : \ A \rightarrow A \otimes A $ , | ||
| + | called comultiplication; the unit $ e \in G $ | ||
| + | gives rise to a homomorphism $ \epsilon : \ A \rightarrow k $ , | ||
| + | called co-unit, and the mapping $ g \mapsto g ^{-1} $ , | ||
| + | $ g \in G $ , | ||
| + | gives rise to a bijective $ k $ - | ||
| + | linear mapping $ S : \ A \rightarrow A \otimes A $ , | ||
| + | called antipode. The group axioms are equivalent to the commutativity of the following diagrams: | ||
| + | $$ | ||
| + | \begin{array}{crcrl} | ||
| + | & & {A \otimes A} & & \\ | ||
| + | {} &\nearrow ^ \Delta & &\searrow ^ { \mathop{\rm id} \otimes \Delta} &{} \\ | ||
| + | A &{} &{} &{} & {A \otimes A \otimes A} \\ | ||
| + | {} &\searrow _ \Delta & &\nearrow _ {\Delta \otimes \mathop{\rm id}} &{} \\ | ||
| + | & & {A \otimes A} & & \\ | ||
| + | \end{array} | ||
| + | $$ | ||
| − | |||
| − | + | $$ | |
| + | \begin{array}{ccc} | ||
| + | A & \stackrel{ { \mathop{\rm id}\nolimits}} \rightarrow & A \\ | ||
| + | {\scriptsize \Delta} \downarrow &{} &\| \\ | ||
| + | {A \otimes A} & \stackrel { \mathop{\rm id}\otimes\epsilon}\rightarrow &{A \otimes k} \\ | ||
| + | \end{array} | ||
| + | \qquad\qquad | ||
| + | \begin{array}{ccc} | ||
| + | A & \stackrel{ { \mathop{\rm id}\nolimits}} \rightarrow & A \\ | ||
| + | {\scriptsize \Delta} \downarrow &{} &\| \\ | ||
| + | {A \otimes A} & \stackrel {\epsilon \otimes \mathop{\rm id} } \rightarrow &{k \otimes A} \\ | ||
| + | \end{array} | ||
| + | $$ | ||
| − | |||
| − | + | $$ | |
| + | \begin{array}{ccccc} | ||
| + | A & \stackrel \Delta \rightarrow A \otimes A & \stackrel{ { \mathop{\rm id}\nolimits \otimes S}} \rightarrow &A \otimes A \rightarrow ^ m & A \\ | ||
| + | {} &\searrow _ \epsilon &{} &\nearrow _{i} &{} \\ | ||
| + | {} &{} & k &{} &{} \\ | ||
| + | \end{array} | ||
| + | $$ | ||
| − | + | $$ | |
| + | \begin{array}{ccccc} | ||
| + | A & \stackrel \Delta \rightarrow A \otimes A & \stackrel{ {S \otimes \mathop{\rm id}\nolimits}} \rightarrow &A \otimes A \rightarrow ^ m & A \\ | ||
| + | {} &\searrow _ \epsilon &{} &\nearrow _{i} &{} \\ | ||
| + | {} &{} & k &{} &{} \\ | ||
| + | \end{array} | ||
| + | $$ | ||
| − | A | + | Here $ m(a \otimes b) = ab $ , |
| + | $ i(c) = c \cdot 1 _{A} $ . | ||
| + | The commutativity of these diagrams means that $ (A ,\ \Delta ,\ \epsilon ,\ S ) $ | ||
| + | is a commutative Hopf algebra. Since the category of groups is anti-equivalent to the category of commutative Hopf algebras, it is natural to define a quantum group as an object of the category dual to the category of (not necessarily commutative) Hopf algebras. | ||
| − | + | A simple class of non-commutative Hopf algebras is formed by the group algebras of non-commutative groups. These Hopf algebras are commutative, i.e. $ \Delta (A) $ | |
| + | is contained in the symmetric part of $ A \otimes A $ . | ||
| + | Essentially, all cocommutative Hopf algebras are group algebras. | ||
| − | + | Here is an example of a Hopf algebra which is neither commutative nor cocommutative. Fix $ n \in \mathbf N $ | |
| + | and $ q \in k $ , | ||
| + | where $ k $ | ||
| + | is a commutative ring. Denote by $ A $ | ||
| + | the associative $ k $ - | ||
| + | algebra with generators $ x _{ij} $ , | ||
| + | $ 1 \leq i,\ j \leq n $ , | ||
| + | and defining relations $ x _{ij} x _{il} = q x _{il} x _{ij} $ | ||
| + | if $ j < l $ , | ||
| + | $ x _{ij} x _{kj} = q x _{kj} x _{ij} $ | ||
| + | if $ i < k $ , | ||
| + | $ x _{il} x _{kj} = x _{kj} x _{il} $ | ||
| + | if $ i < k $ , | ||
| + | $ l > j $ , | ||
| + | $ [ x _{il} ,\ x _{kj} ] = (q ^{-1} -q) x _{ij} x _{kl} $ | ||
| + | if $ i > k $ , | ||
| + | $ l > j $ , | ||
| + | $ \sum _ {i _{1} \dots i _{n}} x _ {1i _{1}} \dots x _ {ni _{n}} \cdot (-q) ^ {l(i _{1} \dots i _{n} )} = 1 $ , | ||
| + | where $ l ( i _{1} \dots i _{n} ) $ | ||
| + | is the number of inversions in the permutation $ ( i _{1} \dots i _{n} ) $ . | ||
| + | Then $ A $ | ||
| + | has a Hopf algebra structure defined by $ \Delta (x _{ij} ) = \sum _{k} x _{ik} \otimes x _{kj} $ . | ||
| + | If $ q =1 $ , | ||
| + | then $ A $ | ||
| + | is the algebra of polynomial functions on $ \mathop{\rm SL}\nolimits (n) $ . | ||
| + | So, in the general case it is natural to consider elements of $ A $ | ||
| + | as "functions on the quantized SLn" . | ||
| − | + | The quantized $ \mathop{\rm SL}\nolimits (n) $ | |
| + | is one of the simplest quantum groups which appear naturally in the theory of quantum integrable systems and, especially, in the quantum inverse-scattering method [[#References|[a2]]]. The development of this method has led to the following quantization technique for constructing non-commutative non-cocommutative Hopf algebras. It is natural to construct them as deformations of commutative Hopf algebras. If a non-commutative deformation $ A $ | ||
| + | of a commutative Hopf algebra $ A _{0} $ | ||
| + | is given, then a Poisson bracket on $ A _{0} $ | ||
| + | is defined by $ \{ a,\ b \} = \mathop{\rm lim}\nolimits _ {h \rightarrow 0} \ h ^{-1} (ab-ba) $ , | ||
| + | where $ h $ | ||
| + | is the deformation parameter and $ ab $ | ||
| + | means the deformed product, which is not commutative. This Poisson bracket has the usual properties (skew-symmetry, Jacobi identity, $ \{ a,\ bc \} = \{ a,\ b \} c + \{ a,\ c \} b $ ) | ||
| + | and is compatible with comultiplication. In other words, $ A _{0} $ | ||
| + | is a Poisson–Hopf algebra. Therefore it is natural to start with a Poisson–Hopf algebra $ A _{0} $ | ||
| + | and then try to quantize it, i.e. to construct a Hopf algebra deformation of $ A _{0} $ | ||
| + | which induces the given Poisson bracket on $ A _{0} $ . | ||
| − | |||
| − | + | Technically it is more convenient to deform not commutative Hopf algebras but cocommutative ones and to start not with a Poisson–Hopf algebra (or a Poisson–Lie group [[#References|[a1]]], which is more or less the same) but with its infinitesimal version, called a Lie bi-algebra . A Lie bi-algebra is a [[Lie algebra|Lie algebra]] $ \mathfrak g $ | |
| + | with a linear mapping $ \phi : \ \mathfrak g \rightarrow \mathfrak g \otimes \mathfrak g $ | ||
| + | such that: 1) $ \phi ^{*} : \ \mathfrak g ^{*} \otimes \mathfrak g ^{*} \rightarrow \mathfrak g ^{*} $ | ||
| + | defines a Lie algebra structure on $ \mathfrak g ^{*} $ ; | ||
| + | and 2) $ \phi $ | ||
| + | is a $ 1 $ - | ||
| + | cocycle ($ \mathfrak g $ | ||
| + | acts on $ \mathfrak g \otimes \mathfrak g $ | ||
| + | by means of the adjoint representation). By definition, a quantization of $ ( \mathfrak g ,\ \phi ) $ | ||
| + | is a Hopf algebra deformation of the [[Universal enveloping algebra|universal enveloping algebra]] $ U \mathfrak g $ | ||
| + | such that $ \delta \mid _ {\mathfrak g} = \phi $ , | ||
| + | where $ \delta : \ U \mathfrak g \rightarrow U \mathfrak g \otimes U \mathfrak g $ | ||
| + | is the Poisson cobracket, defined by $ \delta (a) = \mathop{\rm lim}\nolimits _ {h \rightarrow 0} \ h ^{-1} ( \Delta (a) - \Delta ^ \prime (a)) $ . | ||
| + | Here $ h $ | ||
| + | is the deformation parameter, $ \Delta $ | ||
| + | the deformed comultiplication and $ \Delta ^ \prime $ | ||
| + | the opposite comultiplication. | ||
| − | + | It is not known whether every Lie bi-algebra can be quantized, and usually quantization is not unique. But in several important cases (cf. [[#References|[a1]]], §3, §6) there exists a canonical quantization. In particular, on a [[Kac–Moody algebra|Kac–Moody algebra]] $ \mathfrak g $ | |
| + | with a fixed scalar product $ ( \ ,\ ) $ | ||
| + | there is a canonical Lie bi-algebra structure and this bi-algebra has a canonical quantization $ U _{h} \mathfrak g $ , | ||
| + | as was discovered in [[#References|[a3]]], [[#References|[a4]]], [[#References|[a5]]]. Let $ \mathfrak h $ | ||
| + | be the Cartan subalgebra of $ \mathfrak g $ , | ||
| + | $ H _{i} \in \mathfrak g $ | ||
| + | the images of the simple roots $ \alpha _{i} \in \mathfrak h ^{*} $ . | ||
| + | Then $ U _{h} \mathfrak g $ | ||
| + | is generated by $ \mathfrak h $ | ||
| + | and $ X _{i} ^{+} $ , | ||
| + | $ X _{i} ^{-} $ | ||
| + | with the following defining relations:$$ | ||
| + | [a _{1} ,\ a _{2} ] = 0 \textrm{ for } | ||
| + | a _{1} ,\ a _{2} \in \mathfrak h ; | ||
| + | $$ | ||
| + | $$ | ||
| + | [a ,\ X _{i} ^ \pm ] = \pm \alpha _{i} (a | ||
| + | ) X _{i} ^ \pm \textrm{ for } a \in \mathfrak h ; | ||
| + | $$ | ||
| + | $$ | ||
| + | [ X _{i} ^{+} ,\ X _{j} ^{-} ] = 2 \delta | ||
| + | _{ij} h ^{-1} \ \mathop{\rm sinh}\nolimits ( h H _{i} / 2) . | ||
| + | $$ | ||
| + | Setting $ n = 1-A _{ij} $ , | ||
| + | $ q = \mathop{\rm exp}\nolimits \ h (H _{i} ,\ H _{j} )/2 $ | ||
| + | one has also$$ | ||
| + | \sum _{k=0} ^ n (-1) ^{k} \binom{n}{k} _{q} | ||
| + | q ^ {-k(n-k)/2} (X _{i} ^ \pm ) ^{k} \cdot | ||
| + | X _{j} ^ \pm \cdot (X _{i} ^ \pm ) ^{n-k} = 0 . | ||
| + | $$ | ||
| + | Here $ (A _{ij} ) $ | ||
| + | is the [[Cartan matrix|Cartan matrix]] and $ ( {} _{k} ^{n} ) _{q} $ | ||
| + | is the Gauss polynomial, i.e.,$$ | ||
| + | \binom{n}{k} _{q} = | ||
| − | + | \frac{(q ^{n} -1 ) \dots (q ^{n-k+1} -1)}{( q ^{k} -1 ) \dots (q-1)} | |
| + | . | ||
| + | $$ | ||
| + | The comultiplication in $ U _{h} \mathfrak g $ | ||
| + | is such that $ \Delta (a) = a \otimes 1 + 1 \otimes a $ | ||
| + | for $ a \in \mathfrak h $ | ||
| + | and$$ | ||
| + | \Delta (X _{i} ^ \pm ) = | ||
| + | X _{i} ^ \pm \otimes \mathop{\rm exp}\nolimits \left ( | ||
| + | \frac{hH _{i}}{4} | ||
| + | \right ) + | ||
| + | \mathop{\rm exp}\nolimits \left ( | ||
| + | \frac{-hH _{i}}{4} | ||
| + | \right ) \otimes X _{i} ^ \pm . | ||
| + | $$ | ||
| + | If $ \mathfrak g $ | ||
| + | is a finite-dimensional simple Lie algebra (cf. [[Lie algebra, semi-simple|Lie algebra, semi-simple]]), then the algebra of regular functions on the corresponding simply-connected algebraic group $ G $ | ||
| + | is isomorphic to the subalgebra of $ ( U \mathfrak g ) ^{*} $ | ||
| + | generated by the matrix elements of the finite-dimensional representations of $ U \mathfrak g $ . | ||
| + | Therefore the subalgebra of $ ( U _{h} \mathfrak g ) ^{*} $ | ||
| + | generated by the matrix elements of the finite-dimensional representations of $ U \mathfrak g $ | ||
| + | can be considered as the algebra of functions on a certain quantization of $ G $ . | ||
| + | For instance, the quantized $ \mathop{\rm SL}\nolimits ( n ) $ ( | ||
| + | cf. above) can be obtained in this way. | ||
| − | + | There is an important notion of a quasitriangular Hopf algebra. This is a pair $ (A,\ R) $ | |
| + | where $ A $ | ||
| + | is a Hopf algebra and $ R $ | ||
| + | is an invertible element of $ A \otimes A $ | ||
| + | such that $ ( \Delta \otimes \mathop{\rm id}\nolimits ) (R) = R ^{13} R ^{23} $ , | ||
| + | $ ( \mathop{\rm id}\nolimits \otimes \Delta )(R) = R ^{13} R ^{12} $ , | ||
| + | $ \Delta ^ \prime (a) = R \cdot \Delta ( a ) \cdot R ^{-1} $ | ||
| + | for $ a \in A $ . | ||
| + | Here $ \Delta ^ \prime $ | ||
| + | is the opposite comultiplication and $ R ^{12} $ , | ||
| + | $ R ^{13} $ , | ||
| + | $ R ^{23} $ | ||
| + | are defined as follows: If $ R = \sum _{i} x _{i} \otimes y _{i} $ , | ||
| + | where $ x _{i} ,\ y _{i} \in A $ , | ||
| + | then $ R ^{12} = \sum _{i} x _{i} \otimes y _{i} \otimes 1 $ , | ||
| + | $ R ^{13} = \sum _{i} x _{i} \otimes 1 \otimes y _{i} $ , | ||
| + | $ R ^{23} = \sum _{i} 1 \otimes x _{i} \otimes y _{i} $ . | ||
| + | If $ (A,\ R ) $ | ||
| + | is a quasitriangular Hopf algebra, then $ R $ | ||
| + | satisfies the quantum Yang–Baxter equation (cf. also [[Yang–Baxter equation|Yang–Baxter equation]]), i.e., $ R ^{12} R ^{13} R ^{23} = R ^{23} R ^{13} R ^{12} $ . | ||
| + | It is known (cf. [[#References|[a1]]], §13) that if $ \mathfrak g $ | ||
| + | is a finite-dimensional simple Lie algebra, then $ U _{h} \mathfrak g $ | ||
| + | has a canonical quasitriangular structure, while if $ \mathfrak g $ | ||
| + | is an infinite-dimensional Kac–Moody algebra, then $ U _{h} \mathfrak g $ | ||
| + | has an "almost quasitriangular" structure. | ||
| − | + | If $ (A,\ R) $ | |
| + | is a quasitriangular Hopf algebra over $ k $ | ||
| + | and $ \rho $ | ||
| + | is a representation $ A \rightarrow \mathop{\rm Mat}\nolimits (n,\ k) $ , | ||
| + | then $ {\mathcal R} = ( \rho \otimes \rho )(R) \in \mathop{\rm End}\nolimits (k ^{n} \otimes k ^{n} ) $ | ||
| + | satisfies the quantum Yang–Baxter equation. There is an inverse construction (cf. [[#References|[a6]]], [[#References|[a7]]]), which goes back to the quantum inverse-scattering method: to a matrix solution of the quantum Yang–Baxter equation satisfying a non-degeneracy condition there corresponds a Hopf algebra. Without this condition one can only construct an associative bi-algebra (the difference between a Hopf algebra and an associative bi-algebra is that in the second case there may be no antipode). This bi-algebra is generated by elements $ t _{ij} $ , | ||
| + | $ 1 \leq i,\ j \leq n $ , | ||
| + | with defining relations $ {\mathcal R} T _{1} T _{2} = T _{2} T _{1} {\mathcal R} $ , | ||
| + | where $ T _{1} = T \otimes 1 \in \mathop{\rm End}\nolimits (k ^{n} \otimes k ^{n} ) $ , | ||
| + | $ T _{2} = 1 \otimes T \in \mathop{\rm End}\nolimits (k ^{n} \otimes k ^{n} ) $ , | ||
| + | $ T $ | ||
| + | is the matrix $ (t _{ij} ) $ , | ||
| + | and $ \Delta $ | ||
| + | is defined by $ \Delta (t _{ij} ) = \sum _{k} t _{ik} \otimes t _{kj} $ . | ||
| − | |||
| − | + | Quasitriangular Hopf algebras are a natural tool for the quantum inverse-scattering in method ([[#References|[a1]]], §11). On the other hand, they can be used (cf. [[#References|[a8]]]) to construct invariants of knots (and of more general objects such as links and tangles) generalizing the Jones polynomial [[#References|[a9]]]. More precisely, to an oriented knot $ \gamma \subset \mathbf R ^{3} $ | |
| + | and a quasitriangular Hopf algebra $ (A ,\ R) $ | ||
| + | there corresponds a central element $ z _ \gamma \in A $ . | ||
| − | |||
| − | + | The usual notion of a group has several versions: abstract group, Lie group, topological group, etc. The same is true for quantum groups. The quantum analogue of the notion of a compact group was introduced in [[#References|[a10]]] (the idea is to use $ C ^{*} $ - | |
| − | + | algebras instead of abstract algebras). The quantized $ \mathop{\rm SU}\nolimits (2) $ ( | |
| − | + | cf. [[#References|[a11]]], [[#References|[a12]]]) is a typical example. The notion of a ring group (cf. , [[#References|[a14]]]) and the equivalent notion of a Kac algebra (cf. [[#References|[a15]]], [[#References|[a16]]]) were introduced as an attempt to define a locally compact quantum group. However, these notions are not general enough (the axioms of , [[#References|[a14]]], [[#References|[a15]]] imply that the square of the antipode is the identity mapping, and therefore the quantized $ \mathop{\rm SU}\nolimits (2) $ | |
| − | + | is not a ring group). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The usual notion of a group has several versions: abstract group, Lie group, topological group, etc. The same is true for quantum groups. The quantum analogue of the notion of a compact group was introduced in [[#References|[a10]]] (the idea is to use | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.G. Drinfel'd, "Quantum groups" , ''Proc. Internat. Congress Mathematicians (Berkeley, 1986)'' , '''1''' , Amer. Math. Soc. (1987) pp. 798–820 {{MR|}} {{ZBL|0667.16003}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.D. Faddeev, "Integrable models in (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q076310152.png" />)-dimensional quantum field theory" , ''Lectures in Les Houches, 1982'' , '''Session 39''' , Elsevier (1984) pp. 563–608 {{MR|782509}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Jimbo, "Quantum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q076310153.png" />-matrix for the generalized Toda system" ''Comm. Math. Phys.'' , '''102''' (1986) pp. 537–547 {{MR|824090}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Jimbo, "A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q076310154.png" />-difference analogue of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q076310155.png" /> and the Yang–Baxter equation" ''Letters Math. Phys.'' , '''10''' (1985) pp. 63–69 {{MR|797001}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> V.G. Drinfel'd, "Hopf algebras and the quantum Yang–Baxter equation" ''Soviet Math. Dokl.'' , '''32''' (1985) pp. 254–258 ''Dokl. Akad. Nauk SSSR'' , '''283''' : 5 (1985) pp. 1060–1064 {{MR|}} {{ZBL|0588.17015}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> V.V. Lyubashenko, "Hopf algebras and vector symmetries" ''Russian Math. Surveys'' , '''41''' : 5 (1986) pp. 153–154 ''Uspekhi Mat. Nauk'' , '''41''' : 5 (1986) pp. 185–186 {{MR|0878344}} {{ZBL|0649.16008}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtayan, "Quantization of Lie groups and Lie algebras" ''Algebra and Analysis'' , '''1''' : 1 (1989) pp. 178–206 (In Russian) {{MR|1015339}} {{ZBL|0677.17010}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> N.Yu. Reshetikhin, "Quasitriangular Hopf algebras and invariants of tangles" ''Algebra and Analysis'' , '''1''' : 2 (1989) pp. 169–188 (In Russian) {{MR|}} {{ZBL|0715.17016}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> V.F.R. Jones, "A polynomial invariant for knots via von Neumann algebras" ''Bulletin Amer. Math. Soc.'' , '''12''' (1985) pp. 103–112 {{MR|0766964}} {{ZBL|0564.57006}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> S.L. Woronowich, "Compact matrix pseudogroups" ''Comm. Math. Phys.'' , '''111''' (1987) pp. 613–665 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> S.L. Woronowich, "Twisted SU(2) group. An example of a noncommutative differential calculus" ''Publ. RIMS'' , '''23''' (1987) pp. 117–181</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> L.L. Vaksman, Ya.S. Soibelman, "Function algebra on the quantum group SU(2)" ''Funct. Anal. Appl.'' , '''22''' : 3 (1988) pp. 170–181 ''Funksional. Anal. Prilozhen.'' , '''22''' : 3 (1988) pp. 1–14</TD></TR><TR><TD valign="top">[a13a]</TD> <TD valign="top"> G.I. Kac, "Ring groups and the duality principle I" ''Trans. Moscow Math. Soc.'' , '''12''' (1963) pp. 291–339 ''Trudy Moskov. Mat. Obshch.'' , '''12''' (1963) pp. 295–301 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a13b]</TD> <TD valign="top"> G.I. Kac, "Ring groups and the duality principle II" ''Trans. Moscow Math. Soc.'' , '''13''' (1965) pp. 94–126 ''Trudy Moskov. Mat. Obshch.'' , '''13''' (1965) pp. 84–113 {{MR|}} {{ZBL|0162.45101}} {{ZBL|0144.37903}} </TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> G.I. Kac, L.I. Vainerman, "Nonunimodular ring groups and Hopf–von Neumann algebras" ''Math. USSR Sb.'' , '''23''' (1974) pp. 185–214 ''Mat. Sb.'' , '''94''' : 2 (1974) pp. 194–225; 335 {{MR|0348038}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> M. Enock, J.-M. Schwartz, "Une dualité dans les algèbres de von Neumann" ''Bull. Soc. Math. France'' , '''44''' (1975) pp. 1–44 {{MR|0442710}} {{ZBL|0343.46044}} </TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> J.-M. Schwartz, "Relations entre "ring groups" et algèbres de Kac" ''Bull. Sci. Math. (2)'' , '''100''' (1976) pp. 289–300 {{MR|0473094}} {{ZBL|0343.46043}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.G. Drinfel'd, "Quantum groups" , ''Proc. Internat. Congress Mathematicians (Berkeley, 1986)'' , '''1''' , Amer. Math. Soc. (1987) pp. 798–820 {{MR|}} {{ZBL|0667.16003}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.D. Faddeev, "Integrable models in (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q076310152.png" />)-dimensional quantum field theory" , ''Lectures in Les Houches, 1982'' , '''Session 39''' , Elsevier (1984) pp. 563–608 {{MR|782509}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Jimbo, "Quantum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q076310153.png" />-matrix for the generalized Toda system" ''Comm. Math. Phys.'' , '''102''' (1986) pp. 537–547 {{MR|824090}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Jimbo, "A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q076310154.png" />-difference analogue of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q076310155.png" /> and the Yang–Baxter equation" ''Letters Math. Phys.'' , '''10''' (1985) pp. 63–69 {{MR|797001}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> V.G. Drinfel'd, "Hopf algebras and the quantum Yang–Baxter equation" ''Soviet Math. Dokl.'' , '''32''' (1985) pp. 254–258 ''Dokl. Akad. Nauk SSSR'' , '''283''' : 5 (1985) pp. 1060–1064 {{MR|}} {{ZBL|0588.17015}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> V.V. Lyubashenko, "Hopf algebras and vector symmetries" ''Russian Math. Surveys'' , '''41''' : 5 (1986) pp. 153–154 ''Uspekhi Mat. Nauk'' , '''41''' : 5 (1986) pp. 185–186 {{MR|0878344}} {{ZBL|0649.16008}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtayan, "Quantization of Lie groups and Lie algebras" ''Algebra and Analysis'' , '''1''' : 1 (1989) pp. 178–206 (In Russian) {{MR|1015339}} {{ZBL|0677.17010}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> N.Yu. Reshetikhin, "Quasitriangular Hopf algebras and invariants of tangles" ''Algebra and Analysis'' , '''1''' : 2 (1989) pp. 169–188 (In Russian) {{MR|}} {{ZBL|0715.17016}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> V.F.R. Jones, "A polynomial invariant for knots via von Neumann algebras" ''Bulletin Amer. Math. Soc.'' , '''12''' (1985) pp. 103–112 {{MR|0766964}} {{ZBL|0564.57006}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> S.L. Woronowich, "Compact matrix pseudogroups" ''Comm. Math. Phys.'' , '''111''' (1987) pp. 613–665 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> S.L. Woronowich, "Twisted SU(2) group. An example of a noncommutative differential calculus" ''Publ. RIMS'' , '''23''' (1987) pp. 117–181</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> L.L. Vaksman, Ya.S. Soibelman, "Function algebra on the quantum group SU(2)" ''Funct. Anal. Appl.'' , '''22''' : 3 (1988) pp. 170–181 ''Funksional. Anal. Prilozhen.'' , '''22''' : 3 (1988) pp. 1–14</TD></TR><TR><TD valign="top">[a13a]</TD> <TD valign="top"> G.I. Kac, "Ring groups and the duality principle I" ''Trans. Moscow Math. Soc.'' , '''12''' (1963) pp. 291–339 ''Trudy Moskov. Mat. Obshch.'' , '''12''' (1963) pp. 295–301 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a13b]</TD> <TD valign="top"> G.I. Kac, "Ring groups and the duality principle II" ''Trans. Moscow Math. Soc.'' , '''13''' (1965) pp. 94–126 ''Trudy Moskov. Mat. Obshch.'' , '''13''' (1965) pp. 84–113 {{MR|}} {{ZBL|0162.45101}} {{ZBL|0144.37903}} </TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> G.I. Kac, L.I. Vainerman, "Nonunimodular ring groups and Hopf–von Neumann algebras" ''Math. USSR Sb.'' , '''23''' (1974) pp. 185–214 ''Mat. Sb.'' , '''94''' : 2 (1974) pp. 194–225; 335 {{MR|0348038}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> M. Enock, J.-M. Schwartz, "Une dualité dans les algèbres de von Neumann" ''Bull. Soc. Math. France'' , '''44''' (1975) pp. 1–44 {{MR|0442710}} {{ZBL|0343.46044}} </TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> J.-M. Schwartz, "Relations entre "ring groups" et algèbres de Kac" ''Bull. Sci. Math. (2)'' , '''100''' (1976) pp. 289–300 {{MR|0473094}} {{ZBL|0343.46043}} </TD></TR></table> | ||
Revision as of 19:01, 16 December 2019
The phrase "quantum group" is more or less a synonym for "Hopf algebra" . More precisely, the category of quantum groups is defined in [a1] to be dual to the category of Hopf algebras. This is natural for the following reason. There is the following general principle: The functor $ X \mapsto \{ \textrm{ the algebra of functions on } X \} $ is an anti-equivalence between the category of "spaces" and the category of commutative associative unital algebras, perhaps with some additional structures or properties (this principle becomes a theorem if "space" is understood to be "affine scheme" or "compact topological space" , and "algebra" is understood to mean "C*-algebra" ). So one can translate the definition of a group into the language of algebras: instead of a space $ G $ with an associative operation $ G \times G \rightarrow G $ one obtains a commutative algebra $ A $ over a commutative ring $ k $ with a homomorphism $ \Delta : \ A \rightarrow A \otimes A $ , called comultiplication; the unit $ e \in G $ gives rise to a homomorphism $ \epsilon : \ A \rightarrow k $ , called co-unit, and the mapping $ g \mapsto g ^{-1} $ , $ g \in G $ , gives rise to a bijective $ k $ - linear mapping $ S : \ A \rightarrow A \otimes A $ , called antipode. The group axioms are equivalent to the commutativity of the following diagrams: $$ \begin{array}{crcrl} & & {A \otimes A} & & \\ {} &\nearrow ^ \Delta & &\searrow ^ { \mathop{\rm id} \otimes \Delta} &{} \\ A &{} &{} &{} & {A \otimes A \otimes A} \\ {} &\searrow _ \Delta & &\nearrow _ {\Delta \otimes \mathop{\rm id}} &{} \\ & & {A \otimes A} & & \\ \end{array} $$
$$
\begin{array}{ccc}
A & \stackrel{ { \mathop{\rm id}\nolimits}} \rightarrow & A \\
{\scriptsize \Delta} \downarrow &{} &\| \\
{A \otimes A} & \stackrel { \mathop{\rm id}\otimes\epsilon}\rightarrow &{A \otimes k} \\
\end{array}
\qquad\qquad
\begin{array}{ccc}
A & \stackrel{ { \mathop{\rm id}\nolimits}} \rightarrow & A \\
{\scriptsize \Delta} \downarrow &{} &\| \\
{A \otimes A} & \stackrel {\epsilon \otimes \mathop{\rm id} } \rightarrow &{k \otimes A} \\
\end{array}
$$
$$
\begin{array}{ccccc}
A & \stackrel \Delta \rightarrow A \otimes A & \stackrel{ { \mathop{\rm id}\nolimits \otimes S}} \rightarrow &A \otimes A \rightarrow ^ m & A \\
{} &\searrow _ \epsilon &{} &\nearrow _{i} &{} \\
{} &{} & k &{} &{} \\
\end{array}
$$
$$ \begin{array}{ccccc} A & \stackrel \Delta \rightarrow A \otimes A & \stackrel{ {S \otimes \mathop{\rm id}\nolimits}} \rightarrow &A \otimes A \rightarrow ^ m & A \\ {} &\searrow _ \epsilon &{} &\nearrow _{i} &{} \\ {} &{} & k &{} &{} \\ \end{array} $$
Here $ m(a \otimes b) = ab $ , $ i(c) = c \cdot 1 _{A} $ . The commutativity of these diagrams means that $ (A ,\ \Delta ,\ \epsilon ,\ S ) $ is a commutative Hopf algebra. Since the category of groups is anti-equivalent to the category of commutative Hopf algebras, it is natural to define a quantum group as an object of the category dual to the category of (not necessarily commutative) Hopf algebras.
A simple class of non-commutative Hopf algebras is formed by the group algebras of non-commutative groups. These Hopf algebras are commutative, i.e. $ \Delta (A) $ is contained in the symmetric part of $ A \otimes A $ . Essentially, all cocommutative Hopf algebras are group algebras.
Here is an example of a Hopf algebra which is neither commutative nor cocommutative. Fix $ n \in \mathbf N $ and $ q \in k $ , where $ k $ is a commutative ring. Denote by $ A $ the associative $ k $ - algebra with generators $ x _{ij} $ , $ 1 \leq i,\ j \leq n $ , and defining relations $ x _{ij} x _{il} = q x _{il} x _{ij} $ if $ j < l $ , $ x _{ij} x _{kj} = q x _{kj} x _{ij} $ if $ i < k $ , $ x _{il} x _{kj} = x _{kj} x _{il} $ if $ i < k $ , $ l > j $ , $ [ x _{il} ,\ x _{kj} ] = (q ^{-1} -q) x _{ij} x _{kl} $ if $ i > k $ , $ l > j $ , $ \sum _ {i _{1} \dots i _{n}} x _ {1i _{1}} \dots x _ {ni _{n}} \cdot (-q) ^ {l(i _{1} \dots i _{n} )} = 1 $ , where $ l ( i _{1} \dots i _{n} ) $ is the number of inversions in the permutation $ ( i _{1} \dots i _{n} ) $ . Then $ A $ has a Hopf algebra structure defined by $ \Delta (x _{ij} ) = \sum _{k} x _{ik} \otimes x _{kj} $ . If $ q =1 $ , then $ A $ is the algebra of polynomial functions on $ \mathop{\rm SL}\nolimits (n) $ . So, in the general case it is natural to consider elements of $ A $ as "functions on the quantized SLn" .
The quantized $ \mathop{\rm SL}\nolimits (n) $ is one of the simplest quantum groups which appear naturally in the theory of quantum integrable systems and, especially, in the quantum inverse-scattering method [a2]. The development of this method has led to the following quantization technique for constructing non-commutative non-cocommutative Hopf algebras. It is natural to construct them as deformations of commutative Hopf algebras. If a non-commutative deformation $ A $ of a commutative Hopf algebra $ A _{0} $ is given, then a Poisson bracket on $ A _{0} $ is defined by $ \{ a,\ b \} = \mathop{\rm lim}\nolimits _ {h \rightarrow 0} \ h ^{-1} (ab-ba) $ , where $ h $ is the deformation parameter and $ ab $ means the deformed product, which is not commutative. This Poisson bracket has the usual properties (skew-symmetry, Jacobi identity, $ \{ a,\ bc \} = \{ a,\ b \} c + \{ a,\ c \} b $ ) and is compatible with comultiplication. In other words, $ A _{0} $ is a Poisson–Hopf algebra. Therefore it is natural to start with a Poisson–Hopf algebra $ A _{0} $ and then try to quantize it, i.e. to construct a Hopf algebra deformation of $ A _{0} $ which induces the given Poisson bracket on $ A _{0} $ .
Technically it is more convenient to deform not commutative Hopf algebras but cocommutative ones and to start not with a Poisson–Hopf algebra (or a Poisson–Lie group [a1], which is more or less the same) but with its infinitesimal version, called a Lie bi-algebra . A Lie bi-algebra is a Lie algebra $ \mathfrak g $
with a linear mapping $ \phi : \ \mathfrak g \rightarrow \mathfrak g \otimes \mathfrak g $
such that: 1) $ \phi ^{*} : \ \mathfrak g ^{*} \otimes \mathfrak g ^{*} \rightarrow \mathfrak g ^{*} $
defines a Lie algebra structure on $ \mathfrak g ^{*} $ ;
and 2) $ \phi $
is a $ 1 $ -
cocycle ($ \mathfrak g $
acts on $ \mathfrak g \otimes \mathfrak g $
by means of the adjoint representation). By definition, a quantization of $ ( \mathfrak g ,\ \phi ) $
is a Hopf algebra deformation of the universal enveloping algebra $ U \mathfrak g $
such that $ \delta \mid _ {\mathfrak g} = \phi $ ,
where $ \delta : \ U \mathfrak g \rightarrow U \mathfrak g \otimes U \mathfrak g $
is the Poisson cobracket, defined by $ \delta (a) = \mathop{\rm lim}\nolimits _ {h \rightarrow 0} \ h ^{-1} ( \Delta (a) - \Delta ^ \prime (a)) $ .
Here $ h $
is the deformation parameter, $ \Delta $
the deformed comultiplication and $ \Delta ^ \prime $
the opposite comultiplication.
It is not known whether every Lie bi-algebra can be quantized, and usually quantization is not unique. But in several important cases (cf. [a1], §3, §6) there exists a canonical quantization. In particular, on a Kac–Moody algebra $ \mathfrak g $ with a fixed scalar product $ ( \ ,\ ) $ there is a canonical Lie bi-algebra structure and this bi-algebra has a canonical quantization $ U _{h} \mathfrak g $ , as was discovered in [a3], [a4], [a5]. Let $ \mathfrak h $ be the Cartan subalgebra of $ \mathfrak g $ , $ H _{i} \in \mathfrak g $ the images of the simple roots $ \alpha _{i} \in \mathfrak h ^{*} $ . Then $ U _{h} \mathfrak g $ is generated by $ \mathfrak h $ and $ X _{i} ^{+} $ , $ X _{i} ^{-} $ with the following defining relations:$$ [a _{1} ,\ a _{2} ] = 0 \textrm{ for } a _{1} ,\ a _{2} \in \mathfrak h ; $$ $$ [a ,\ X _{i} ^ \pm ] = \pm \alpha _{i} (a ) X _{i} ^ \pm \textrm{ for } a \in \mathfrak h ; $$ $$ [ X _{i} ^{+} ,\ X _{j} ^{-} ] = 2 \delta _{ij} h ^{-1} \ \mathop{\rm sinh}\nolimits ( h H _{i} / 2) . $$ Setting $ n = 1-A _{ij} $ , $ q = \mathop{\rm exp}\nolimits \ h (H _{i} ,\ H _{j} )/2 $ one has also$$ \sum _{k=0} ^ n (-1) ^{k} \binom{n}{k} _{q} q ^ {-k(n-k)/2} (X _{i} ^ \pm ) ^{k} \cdot X _{j} ^ \pm \cdot (X _{i} ^ \pm ) ^{n-k} = 0 . $$ Here $ (A _{ij} ) $ is the Cartan matrix and $ ( {} _{k} ^{n} ) _{q} $ is the Gauss polynomial, i.e.,$$ \binom{n}{k} _{q} = \frac{(q ^{n} -1 ) \dots (q ^{n-k+1} -1)}{( q ^{k} -1 ) \dots (q-1)} . $$ The comultiplication in $ U _{h} \mathfrak g $ is such that $ \Delta (a) = a \otimes 1 + 1 \otimes a $ for $ a \in \mathfrak h $ and$$ \Delta (X _{i} ^ \pm ) = X _{i} ^ \pm \otimes \mathop{\rm exp}\nolimits \left ( \frac{hH _{i}}{4} \right ) + \mathop{\rm exp}\nolimits \left ( \frac{-hH _{i}}{4} \right ) \otimes X _{i} ^ \pm . $$ If $ \mathfrak g $ is a finite-dimensional simple Lie algebra (cf. Lie algebra, semi-simple), then the algebra of regular functions on the corresponding simply-connected algebraic group $ G $ is isomorphic to the subalgebra of $ ( U \mathfrak g ) ^{*} $ generated by the matrix elements of the finite-dimensional representations of $ U \mathfrak g $ . Therefore the subalgebra of $ ( U _{h} \mathfrak g ) ^{*} $ generated by the matrix elements of the finite-dimensional representations of $ U \mathfrak g $ can be considered as the algebra of functions on a certain quantization of $ G $ . For instance, the quantized $ \mathop{\rm SL}\nolimits ( n ) $ ( cf. above) can be obtained in this way.
There is an important notion of a quasitriangular Hopf algebra. This is a pair $ (A,\ R) $ where $ A $ is a Hopf algebra and $ R $ is an invertible element of $ A \otimes A $ such that $ ( \Delta \otimes \mathop{\rm id}\nolimits ) (R) = R ^{13} R ^{23} $ , $ ( \mathop{\rm id}\nolimits \otimes \Delta )(R) = R ^{13} R ^{12} $ , $ \Delta ^ \prime (a) = R \cdot \Delta ( a ) \cdot R ^{-1} $ for $ a \in A $ . Here $ \Delta ^ \prime $ is the opposite comultiplication and $ R ^{12} $ , $ R ^{13} $ , $ R ^{23} $ are defined as follows: If $ R = \sum _{i} x _{i} \otimes y _{i} $ , where $ x _{i} ,\ y _{i} \in A $ , then $ R ^{12} = \sum _{i} x _{i} \otimes y _{i} \otimes 1 $ , $ R ^{13} = \sum _{i} x _{i} \otimes 1 \otimes y _{i} $ , $ R ^{23} = \sum _{i} 1 \otimes x _{i} \otimes y _{i} $ . If $ (A,\ R ) $ is a quasitriangular Hopf algebra, then $ R $ satisfies the quantum Yang–Baxter equation (cf. also Yang–Baxter equation), i.e., $ R ^{12} R ^{13} R ^{23} = R ^{23} R ^{13} R ^{12} $ . It is known (cf. [a1], §13) that if $ \mathfrak g $ is a finite-dimensional simple Lie algebra, then $ U _{h} \mathfrak g $ has a canonical quasitriangular structure, while if $ \mathfrak g $ is an infinite-dimensional Kac–Moody algebra, then $ U _{h} \mathfrak g $ has an "almost quasitriangular" structure.
If $ (A,\ R) $ is a quasitriangular Hopf algebra over $ k $ and $ \rho $ is a representation $ A \rightarrow \mathop{\rm Mat}\nolimits (n,\ k) $ , then $ {\mathcal R} = ( \rho \otimes \rho )(R) \in \mathop{\rm End}\nolimits (k ^{n} \otimes k ^{n} ) $ satisfies the quantum Yang–Baxter equation. There is an inverse construction (cf. [a6], [a7]), which goes back to the quantum inverse-scattering method: to a matrix solution of the quantum Yang–Baxter equation satisfying a non-degeneracy condition there corresponds a Hopf algebra. Without this condition one can only construct an associative bi-algebra (the difference between a Hopf algebra and an associative bi-algebra is that in the second case there may be no antipode). This bi-algebra is generated by elements $ t _{ij} $ , $ 1 \leq i,\ j \leq n $ , with defining relations $ {\mathcal R} T _{1} T _{2} = T _{2} T _{1} {\mathcal R} $ , where $ T _{1} = T \otimes 1 \in \mathop{\rm End}\nolimits (k ^{n} \otimes k ^{n} ) $ , $ T _{2} = 1 \otimes T \in \mathop{\rm End}\nolimits (k ^{n} \otimes k ^{n} ) $ , $ T $ is the matrix $ (t _{ij} ) $ , and $ \Delta $ is defined by $ \Delta (t _{ij} ) = \sum _{k} t _{ik} \otimes t _{kj} $ .
Quasitriangular Hopf algebras are a natural tool for the quantum inverse-scattering in method ([a1], §11). On the other hand, they can be used (cf. [a8]) to construct invariants of knots (and of more general objects such as links and tangles) generalizing the Jones polynomial [a9]. More precisely, to an oriented knot $ \gamma \subset \mathbf R ^{3} $
and a quasitriangular Hopf algebra $ (A ,\ R) $
there corresponds a central element $ z _ \gamma \in A $ .
The usual notion of a group has several versions: abstract group, Lie group, topological group, etc. The same is true for quantum groups. The quantum analogue of the notion of a compact group was introduced in [a10] (the idea is to use $ C ^{*} $ -
algebras instead of abstract algebras). The quantized $ \mathop{\rm SU}\nolimits (2) $ (
cf. [a11], [a12]) is a typical example. The notion of a ring group (cf. , [a14]) and the equivalent notion of a Kac algebra (cf. [a15], [a16]) were introduced as an attempt to define a locally compact quantum group. However, these notions are not general enough (the axioms of , [a14], [a15] imply that the square of the antipode is the identity mapping, and therefore the quantized $ \mathop{\rm SU}\nolimits (2) $
is not a ring group).
References
| [a1] | V.G. Drinfel'd, "Quantum groups" , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , 1 , Amer. Math. Soc. (1987) pp. 798–820 Zbl 0667.16003 |
| [a2] | L.D. Faddeev, "Integrable models in (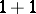 )-dimensional quantum field theory" , Lectures in Les Houches, 1982 , Session 39 , Elsevier (1984) pp. 563–608 MR782509 )-dimensional quantum field theory" , Lectures in Les Houches, 1982 , Session 39 , Elsevier (1984) pp. 563–608 MR782509 |
| [a3] | M. Jimbo, "Quantum 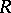 -matrix for the generalized Toda system" Comm. Math. Phys. , 102 (1986) pp. 537–547 MR824090 -matrix for the generalized Toda system" Comm. Math. Phys. , 102 (1986) pp. 537–547 MR824090 |
| [a4] | M. Jimbo, "A 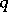 -difference analogue of -difference analogue of 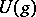 and the Yang–Baxter equation" Letters Math. Phys. , 10 (1985) pp. 63–69 MR797001 and the Yang–Baxter equation" Letters Math. Phys. , 10 (1985) pp. 63–69 MR797001 |
| [a5] | V.G. Drinfel'd, "Hopf algebras and the quantum Yang–Baxter equation" Soviet Math. Dokl. , 32 (1985) pp. 254–258 Dokl. Akad. Nauk SSSR , 283 : 5 (1985) pp. 1060–1064 Zbl 0588.17015 |
| [a6] | V.V. Lyubashenko, "Hopf algebras and vector symmetries" Russian Math. Surveys , 41 : 5 (1986) pp. 153–154 Uspekhi Mat. Nauk , 41 : 5 (1986) pp. 185–186 MR0878344 Zbl 0649.16008 |
| [a7] | L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtayan, "Quantization of Lie groups and Lie algebras" Algebra and Analysis , 1 : 1 (1989) pp. 178–206 (In Russian) MR1015339 Zbl 0677.17010 |
| [a8] | N.Yu. Reshetikhin, "Quasitriangular Hopf algebras and invariants of tangles" Algebra and Analysis , 1 : 2 (1989) pp. 169–188 (In Russian) Zbl 0715.17016 |
| [a9] | V.F.R. Jones, "A polynomial invariant for knots via von Neumann algebras" Bulletin Amer. Math. Soc. , 12 (1985) pp. 103–112 MR0766964 Zbl 0564.57006 |
| [a10] | S.L. Woronowich, "Compact matrix pseudogroups" Comm. Math. Phys. , 111 (1987) pp. 613–665 |
| [a11] | S.L. Woronowich, "Twisted SU(2) group. An example of a noncommutative differential calculus" Publ. RIMS , 23 (1987) pp. 117–181 |
| [a12] | L.L. Vaksman, Ya.S. Soibelman, "Function algebra on the quantum group SU(2)" Funct. Anal. Appl. , 22 : 3 (1988) pp. 170–181 Funksional. Anal. Prilozhen. , 22 : 3 (1988) pp. 1–14 |
| [a13a] | G.I. Kac, "Ring groups and the duality principle I" Trans. Moscow Math. Soc. , 12 (1963) pp. 291–339 Trudy Moskov. Mat. Obshch. , 12 (1963) pp. 295–301 |
| [a13b] | G.I. Kac, "Ring groups and the duality principle II" Trans. Moscow Math. Soc. , 13 (1965) pp. 94–126 Trudy Moskov. Mat. Obshch. , 13 (1965) pp. 84–113 Zbl 0162.45101 Zbl 0144.37903 |
| [a14] | G.I. Kac, L.I. Vainerman, "Nonunimodular ring groups and Hopf–von Neumann algebras" Math. USSR Sb. , 23 (1974) pp. 185–214 Mat. Sb. , 94 : 2 (1974) pp. 194–225; 335 MR0348038 |
| [a15] | M. Enock, J.-M. Schwartz, "Une dualité dans les algèbres de von Neumann" Bull. Soc. Math. France , 44 (1975) pp. 1–44 MR0442710 Zbl 0343.46044 |
| [a16] | J.-M. Schwartz, "Relations entre "ring groups" et algèbres de Kac" Bull. Sci. Math. (2) , 100 (1976) pp. 289–300 MR0473094 Zbl 0343.46043 |
Quantum groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantum_groups&oldid=44257