Principal homogeneous space
A principal 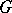 -object in the category of algebraic varieties or schemes. If
-object in the category of algebraic varieties or schemes. If 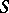 is a scheme and
is a scheme and 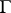 is a group scheme over
is a group scheme over  , then a principal
, then a principal 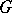 -object in the category of schemes over
-object in the category of schemes over 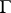 is said to be a principal homogeneous space. If
is said to be a principal homogeneous space. If 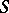 is the spectrum of a field
is the spectrum of a field 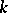 (cf. Spectrum of a ring) and
(cf. Spectrum of a ring) and 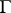 is an algebraic
is an algebraic 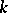 -group (cf. Algebraic group), then a principal homogeneous space over
-group (cf. Algebraic group), then a principal homogeneous space over 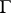 is an algebraic
is an algebraic 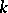 -variety
-variety 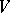 acted upon (from the left) by
acted upon (from the left) by 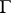 such that if
such that if 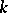 is replaced by its separable algebraic closure
is replaced by its separable algebraic closure 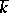 , then each point
, then each point 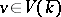 defines an isomorphic mapping
defines an isomorphic mapping 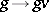 of the varieties
of the varieties 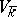 and
and 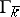 . A principal homogeneous space
. A principal homogeneous space 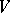 is trivial if and only if
is trivial if and only if 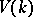 is non-empty. The set of classes of isomorphic principal homogeneous spaces over a smooth algebraic group
is non-empty. The set of classes of isomorphic principal homogeneous spaces over a smooth algebraic group 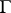 can be identified with the set of Galois cohomology
can be identified with the set of Galois cohomology 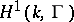 . In the general case the set of classes of principal homogeneous spaces over an
. In the general case the set of classes of principal homogeneous spaces over an 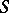 -group scheme
-group scheme 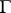 coincides with the set of one-dimensional non-Abelian cohomology
coincides with the set of one-dimensional non-Abelian cohomology 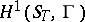 . Here
. Here 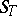 is some Grothendieck topology on the scheme
is some Grothendieck topology on the scheme 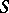 [2].
[2].
Principal homogeneous spaces have been computed in a number of cases. If 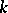 is a finite field, then each principal homogeneous space over a connected algebraic
is a finite field, then each principal homogeneous space over a connected algebraic 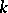 -group is trivial (Lang's theorem). This theorem also holds if
-group is trivial (Lang's theorem). This theorem also holds if 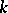 is a
is a 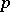 -adic number field and
-adic number field and 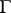 is a simply-connected semi-simple group (Kneser's theorem). If
is a simply-connected semi-simple group (Kneser's theorem). If 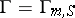 is a multiplicative
is a multiplicative 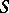 -group scheme, then the set of classes of principal homogeneous spaces over
-group scheme, then the set of classes of principal homogeneous spaces over 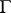 becomes identical with the Picard group
becomes identical with the Picard group 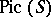 of
of 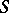 . In particular, if
. In particular, if  is the spectrum of a field, this group is trivial. If
is the spectrum of a field, this group is trivial. If  is an additive
is an additive 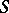 -group scheme, then the set of classes of principal homogeneous spaces over
-group scheme, then the set of classes of principal homogeneous spaces over 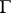 becomes identical with the one-dimensional cohomology group
becomes identical with the one-dimensional cohomology group 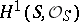 of the structure sheaf
of the structure sheaf 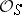 of
of 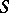 . In particular, this set is trivial if
. In particular, this set is trivial if 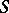 is an affine scheme. If
is an affine scheme. If 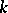 is a global field (i.e. an algebraic number field or a field of algebraic functions in one variable), then the study of the set of classes of principal homogeneous spaces over an algebraic
is a global field (i.e. an algebraic number field or a field of algebraic functions in one variable), then the study of the set of classes of principal homogeneous spaces over an algebraic 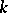 -group
-group 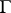 is based on the study of the Tate–Shafarevich set
is based on the study of the Tate–Shafarevich set 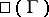 , which consists of the principal homogeneous spaces over
, which consists of the principal homogeneous spaces over 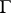 with rational points in all completions
with rational points in all completions 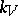 with respect to the valuations of
with respect to the valuations of 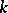 . If
. If 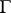 is an Abelian group over the field
is an Abelian group over the field 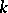 , then the set of classes of principal homogeneous spaces over
, then the set of classes of principal homogeneous spaces over 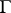 forms a group (cf. Weil–Châtelet group).
forms a group (cf. Weil–Châtelet group).
References
| [1] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1973) |
| [2] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson (1970) |
| [3] | S. Lang, J. Tate, "Principal homogeneous spaces over abelian varieties" Amer. J. Math. , 80 (1958) pp. 659–684 |
Comments
The notion of a principal homogeneous space is not restricted to algebraic geometry. For instance, it is defined in the category of 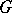 -sets, where
-sets, where  is a group. Let
is a group. Let 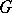 be a finite (profinite, etc.) group. Let
be a finite (profinite, etc.) group. Let 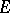 be a
be a 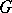 -set, i.e. a set
-set, i.e. a set 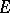 with an action
with an action 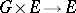 of
of 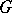 on it. Let
on it. Let 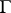 be a
be a 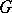 -group, i.e. a group object in the category of
-group, i.e. a group object in the category of 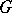 -sets, which means that
-sets, which means that 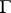 is a group and that the action of
is a group and that the action of 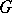 on
on 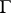 is by group automorphisms of
is by group automorphisms of 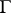 :
: 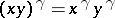 for
for 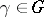 ,
, 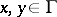 . One says that
. One says that 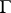 operates compatibly with the
operates compatibly with the 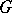 -action from the left on
-action from the left on 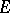 if there is a
if there is a 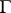 -action
-action 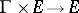 on
on 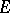 such that
such that  for
for  ,
,  ,
, 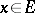 . A principal homogeneous space over
. A principal homogeneous space over 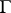 in this setting is a
in this setting is a 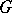 -set
-set 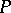 on which
on which 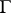 acts compatibly with the
acts compatibly with the 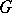 -action and such that for all
-action and such that for all 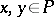 there is a
there is a 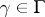 such that
such that 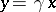 . (This is the property to which the word "principal" refers; one also says that
. (This is the property to which the word "principal" refers; one also says that 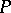 is an affine space over
is an affine space over 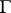 .) In this case there is a natural bijective correspondence between
.) In this case there is a natural bijective correspondence between 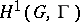 and isomorphism classes of principal homogeneous spaces over
and isomorphism classes of principal homogeneous spaces over 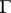 and, in fact,
and, in fact, 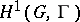 (for non-Abelian
(for non-Abelian  ) is sometimes defined this way.
) is sometimes defined this way.
Principal homogeneous space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principal_homogeneous_space&oldid=16675