Difference between revisions of "Primitive recursive function"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48286 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
A function from natural numbers to natural numbers which can be obtained from the initial functions | A function from natural numbers to natural numbers which can be obtained from the initial functions | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p0746101.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
by a finite number of the operations of composition and [[Primitive recursion|primitive recursion]]. | by a finite number of the operations of composition and [[Primitive recursion|primitive recursion]]. | ||
| − | Since the initial functions are computable and the operators of superposition and primitive recursion preserve computability, the set of all primitive recursive functions is a subclass of the class of all computable functions (cf. [[Computable function|Computable function]]). Every primitive recursive function is specified by a description of its construction from the initial functions (a primitive recursive description); hence the class of primitive recursive functions is countable. Practically all arithmetic functions used in mathematics for some concrete reason are primitive recursive functions; e.g. | + | Since the initial functions are computable and the operators of superposition and primitive recursion preserve computability, the set of all primitive recursive functions is a subclass of the class of all computable functions (cf. [[Computable function|Computable function]]). Every primitive recursive function is specified by a description of its construction from the initial functions (a primitive recursive description); hence the class of primitive recursive functions is countable. Practically all arithmetic functions used in mathematics for some concrete reason are primitive recursive functions; e.g. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p0746102.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p0746103.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p0746104.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p0746105.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p0746106.png" /> (the remainder from division of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p0746107.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p0746108.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p0746109.png" /> (the prime number with index <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461010.png" />), etc. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | the remainder from division of | ||
| − | by | ||
| − | |||
| − | the prime number with index | ||
| − | etc. | ||
| − | A relation | + | A relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461011.png" /> on natural numbers is called a primitive recursive relation if the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461012.png" />, equal to 1 if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461013.png" /> is true and 0 if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461014.png" /> is false, is primitive recursive. One says that the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461015.png" /> has been obtained from a relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461016.png" /> by means of a bounded quantifier if |
| − | on natural numbers is called a primitive recursive relation if the function | ||
| − | equal to 1 if | ||
| − | is true and 0 if | ||
| − | is false, is primitive recursive. One says that the relation | ||
| − | has been obtained from a relation | ||
| − | by means of a bounded quantifier if | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461017.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
or | or | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461018.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
The class of primitive recursive relations is closed under the application of logical connectives (including negation) and bounded quantifiers. | The class of primitive recursive relations is closed under the application of logical connectives (including negation) and bounded quantifiers. | ||
| − | Suppose that | + | Suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461019.png" /> are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461020.png" />-place primitive recursive functions, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461021.png" /> be primitive recursive relations such that for any set of argument values at most one of them is true. Then the function |
| − | are | ||
| − | place primitive recursive functions, and let | ||
| − | be primitive recursive relations such that for any set of argument values at most one of them is true. Then the function | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461022.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | |||
is primitive recursive. | is primitive recursive. | ||
| − | One says that the function | + | One says that the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461023.png" /> has been obtained from an everywhere-defined function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461024.png" /> by means of the bounded minimization operator if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461025.png" /> is equal to the minimal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461026.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461027.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461028.png" />, and is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461029.png" /> otherwise. The class of primitive recursive functions is closed under bounded minimization operators. |
| − | has been obtained from an everywhere-defined function | ||
| − | by means of the bounded minimization operator if | ||
| − | is equal to the minimal | ||
| − | such that | ||
| − | and | ||
| − | and is equal to | ||
| − | otherwise. The class of primitive recursive functions is closed under bounded minimization operators. | ||
| − | A function | + | A function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461030.png" /> is called universal for the class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461031.png" />-place primitive recursive functions if for each such function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461032.png" /> there is a natural number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461033.png" /> such that |
| − | is called universal for the class of | ||
| − | place primitive recursive functions if for each such function | ||
| − | there is a natural number | ||
| − | such that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461034.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | There exists a universal function for every | + | There exists a universal function for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461035.png" />, but it need not be primitive recursive. |
| − | but it need not be primitive recursive. | ||
| − | Every recursively enumerable set is the range of values of a primitive recursive function; every recursively enumerable relation | + | Every recursively enumerable set is the range of values of a primitive recursive function; every recursively enumerable relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461036.png" /> can be represented as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461037.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461038.png" /> is a primitive recursive relation. Every primitive recursive function can be represented in formal arithmetic (cf. [[Arithmetic, formal|Arithmetic, formal]]); i.e. for each primitive recursive function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461039.png" /> there is an arithmetical formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461040.png" /> such that for all natural numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461041.png" />, the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461042.png" /> is derivable in formal arithmetic if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461043.png" />, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461044.png" /> is derivable if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461045.png" />. (Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461046.png" /> are arithmetical terms reflecting the natural numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074610/p07461047.png" /> in formal arithmetic.) This fact takes a central position in the proof of the incompleteness of formal arithmetic (cf. [[#References|[4]]]). |
| − | can be represented as | ||
| − | where | ||
| − | is a primitive recursive relation. Every primitive recursive function can be represented in formal arithmetic (cf. [[Arithmetic, formal|Arithmetic, formal]]); i.e. for each primitive recursive function | ||
| − | there is an arithmetical formula | ||
| − | such that for all natural numbers | ||
| − | the formula | ||
| − | is derivable in formal arithmetic if | ||
| − | while | ||
| − | is derivable if | ||
| − | (Here | ||
| − | are arithmetical terms reflecting the natural numbers | ||
| − | in formal arithmetic.) This fact takes a central position in the proof of the incompleteness of formal arithmetic (cf. [[#References|[4]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.A. Uspenskii, "Leçons sur les fonctions calculables" , Hermann (1966) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.I. Mal'tsev, "Algorithms and recursive functions" , Wolters-Noordhoff (1970) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E. Mendelson, "Introduction to mathematical logic" , v. Nostrand (1964)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.A. Uspenskii, "Leçons sur les fonctions calculables" , Hermann (1966) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.I. Mal'tsev, "Algorithms and recursive functions" , Wolters-Noordhoff (1970) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E. Mendelson, "Introduction to mathematical logic" , v. Nostrand (1964)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
Revision as of 14:52, 7 June 2020
A function from natural numbers to natural numbers which can be obtained from the initial functions
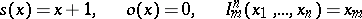 |
by a finite number of the operations of composition and primitive recursion.
Since the initial functions are computable and the operators of superposition and primitive recursion preserve computability, the set of all primitive recursive functions is a subclass of the class of all computable functions (cf. Computable function). Every primitive recursive function is specified by a description of its construction from the initial functions (a primitive recursive description); hence the class of primitive recursive functions is countable. Practically all arithmetic functions used in mathematics for some concrete reason are primitive recursive functions; e.g. 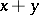 ,
, 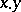 ,
, 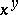 ,
, 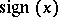 ,
, 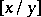 (the remainder from division of
(the remainder from division of  by
by 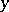 ),
),  (the prime number with index
(the prime number with index  ), etc.
), etc.
A relation  on natural numbers is called a primitive recursive relation if the function
on natural numbers is called a primitive recursive relation if the function 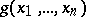 , equal to 1 if
, equal to 1 if 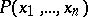 is true and 0 if
is true and 0 if 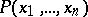 is false, is primitive recursive. One says that the relation
is false, is primitive recursive. One says that the relation 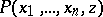 has been obtained from a relation
has been obtained from a relation 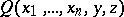 by means of a bounded quantifier if
by means of a bounded quantifier if
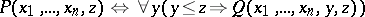 |
or
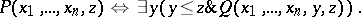 |
The class of primitive recursive relations is closed under the application of logical connectives (including negation) and bounded quantifiers.
Suppose that 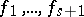 are
are  -place primitive recursive functions, and let
-place primitive recursive functions, and let 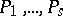 be primitive recursive relations such that for any set of argument values at most one of them is true. Then the function
be primitive recursive relations such that for any set of argument values at most one of them is true. Then the function
 | (*) |
is primitive recursive.
One says that the function 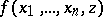 has been obtained from an everywhere-defined function
has been obtained from an everywhere-defined function 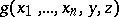 by means of the bounded minimization operator if
by means of the bounded minimization operator if 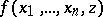 is equal to the minimal
is equal to the minimal  such that
such that 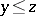 and
and 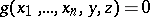 , and is equal to
, and is equal to 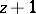 otherwise. The class of primitive recursive functions is closed under bounded minimization operators.
otherwise. The class of primitive recursive functions is closed under bounded minimization operators.
A function 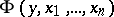 is called universal for the class of
is called universal for the class of  -place primitive recursive functions if for each such function
-place primitive recursive functions if for each such function 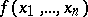 there is a natural number
there is a natural number 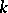 such that
such that
 |
There exists a universal function for every 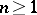 , but it need not be primitive recursive.
, but it need not be primitive recursive.
Every recursively enumerable set is the range of values of a primitive recursive function; every recursively enumerable relation 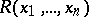 can be represented as
can be represented as 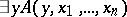 , where
, where 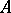 is a primitive recursive relation. Every primitive recursive function can be represented in formal arithmetic (cf. Arithmetic, formal); i.e. for each primitive recursive function
is a primitive recursive relation. Every primitive recursive function can be represented in formal arithmetic (cf. Arithmetic, formal); i.e. for each primitive recursive function 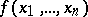 there is an arithmetical formula
there is an arithmetical formula  such that for all natural numbers
such that for all natural numbers 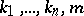 , the formula
, the formula 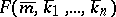 is derivable in formal arithmetic if
is derivable in formal arithmetic if 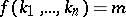 , while
, while 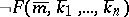 is derivable if
is derivable if 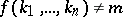 . (Here
. (Here 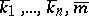 are arithmetical terms reflecting the natural numbers
are arithmetical terms reflecting the natural numbers 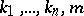 in formal arithmetic.) This fact takes a central position in the proof of the incompleteness of formal arithmetic (cf. [4]).
in formal arithmetic.) This fact takes a central position in the proof of the incompleteness of formal arithmetic (cf. [4]).
References
| [1] | V.A. Uspenskii, "Leçons sur les fonctions calculables" , Hermann (1966) (Translated from Russian) |
| [2] | A.I. Mal'tsev, "Algorithms and recursive functions" , Wolters-Noordhoff (1970) (Translated from Russian) |
| [3] | H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165 |
| [4] | E. Mendelson, "Introduction to mathematical logic" , v. Nostrand (1964) |
Comments
The fact that the function (*) is primitive recursive under the given assumptions is often rephrased as: the class of primitive recursive functions is closed under "definition by cases" .
References
| [a1] | C. Calude, "Theories of computational complexity" , North-Holland (1988) |
Primitive recursive function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primitive_recursive_function&oldid=49374