Pre-compact space
From Encyclopedia of Mathematics
totally-bounded space
A uniform space 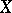 for all entourages
for all entourages 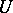 of which there exists a finite covering of
of which there exists a finite covering of 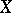 by sets of
by sets of 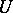 . In other words, for every entourage
. In other words, for every entourage 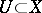 there is a finite subset
there is a finite subset 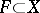 such that
such that 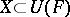 . A uniform space is pre-compact if and only if every net (cf. Net (of sets in a topological space)) in
. A uniform space is pre-compact if and only if every net (cf. Net (of sets in a topological space)) in 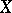 has a Cauchy subnet. Therefore, for
has a Cauchy subnet. Therefore, for 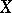 to be a pre-compact space it is sufficient that some completion of
to be a pre-compact space it is sufficient that some completion of 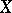 is compact, and it is necessary that every completion of it is compact (cf. Completion of a uniform space).
is compact, and it is necessary that every completion of it is compact (cf. Completion of a uniform space).
Comments
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
How to Cite This Entry:
Pre-compact space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pre-compact_space&oldid=14489
Pre-compact space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pre-compact_space&oldid=14489
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article