Pre-Hilbert space
A vector space  over the field of complex or real numbers equipped with a scalar product
over the field of complex or real numbers equipped with a scalar product  ,
,  , satisfying the following conditions:
, satisfying the following conditions:
1)  ,
,  ,
,  ,
,  ,
,  (
( );
);
2) 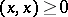 for
for 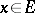 ;
;
3) 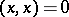 if and only if
if and only if 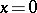 .
.
On a pre-Hilbert space a norm 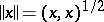 is defined. The completion of
is defined. The completion of 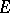 with respect to this norm is a Hilbert space.
with respect to this norm is a Hilbert space.
Comments
A function 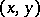 as above is also called an inner product. If it satisfies only 1) and 2) it is sometimes called a pre-inner product. Accordingly, pre-Hilbert spaces are sometimes called inner product spaces, while vector spaces with a pre-inner product are also called pre-inner product spaces.
as above is also called an inner product. If it satisfies only 1) and 2) it is sometimes called a pre-inner product. Accordingly, pre-Hilbert spaces are sometimes called inner product spaces, while vector spaces with a pre-inner product are also called pre-inner product spaces.
If 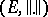 is a normed linear space, then it has an inner product generating the norm if (and only if) the norm satisfies the parallelogram law
is a normed linear space, then it has an inner product generating the norm if (and only if) the norm satisfies the parallelogram law
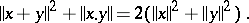 |
For the characterizations of inner product spaces see [a1], Chapt. 4.
References
| [a1] | V.I. Istrăţescu, "Inner product structures" , Reidel (1987) |
| [a2] | W. Rudin, "Functional analysis" , McGraw-Hill (1979) |
| [a3] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 |
Pre-Hilbert space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pre-Hilbert_space&oldid=15523