Positive-definite kernel
A complex-valued function  on
on  , where
, where 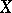 is any set, which satisfies the condition
is any set, which satisfies the condition
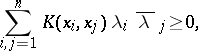 |
for any  ,
,  ,
, 
 . The measurable positive-definite kernels on a measure space
. The measurable positive-definite kernels on a measure space  correspond to the positive integral operators (cf. Integral operator) on
correspond to the positive integral operators (cf. Integral operator) on  ; in order to include arbitrary positive operators in this correspondence one has to introduce generalized positive-definite kernels, which are associated with Hilbert spaces [1].
; in order to include arbitrary positive operators in this correspondence one has to introduce generalized positive-definite kernels, which are associated with Hilbert spaces [1].
The theory of positive-definite kernels extends the theory of positive-definite functions (cf. Positive-definite function) on groups: For a function 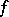 on a group
on a group 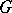 to be positive definite it is necessary and sufficient that the function
to be positive definite it is necessary and sufficient that the function 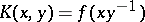 on
on 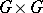 is a positive-definite kernel. In particular, certain results from the theory of positive-definite functions can be extended to positive-definite kernels. For example, Bochner's theorem is that each positive-definite function is the Fourier transform of a positive bounded measure (i.e. an integral linear combination of characters), and this is generalized as follows: Each (generalized) positive-definite kernel has an integral representation by means of so-called elementary positive-definite kernels with respect to a given differential expression [1].
is a positive-definite kernel. In particular, certain results from the theory of positive-definite functions can be extended to positive-definite kernels. For example, Bochner's theorem is that each positive-definite function is the Fourier transform of a positive bounded measure (i.e. an integral linear combination of characters), and this is generalized as follows: Each (generalized) positive-definite kernel has an integral representation by means of so-called elementary positive-definite kernels with respect to a given differential expression [1].
References
| [1] | Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [2a] | M.G. Krein, "Hermitian positive kernels on homogeneous spaces I" Ukr. Mat. Zh. , 1 : 4 (1949) pp. 64–98 (In Russian) |
| [2b] | M.G. Krein, "Hermitian positive kernels on homogeneous spaces II" Ukr. Mat. Zh. , 2 : 1 (1950) pp. 10–59 (In Russian) |
Comments
References
| [a1] | H. Reiter, "Classical harmonic analysis and locally compact groups" , Oxford Univ. Press (1968) |
Positive-definite kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive-definite_kernel&oldid=11204