Poly-harmonic function
hyper-harmonic function, meta-harmonic function, of order 
A function  of real variables defined in a region
of real variables defined in a region  of a Euclidean space
of a Euclidean space  ,
,  , having continuous partial derivatives up to and including the order
, having continuous partial derivatives up to and including the order  and satisfying the poly-harmonic equation everywhere in
and satisfying the poly-harmonic equation everywhere in  :
:
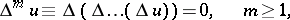 |
where 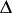 is the Laplace operator. For
is the Laplace operator. For  one obtains harmonic functions (cf. Harmonic function), while for
one obtains harmonic functions (cf. Harmonic function), while for 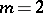 one obtains biharmonic functions (cf. Biharmonic function). Each poly-harmonic function is an analytic function of the coordinates
one obtains biharmonic functions (cf. Biharmonic function). Each poly-harmonic function is an analytic function of the coordinates  . Some other properties of harmonic functions also carry over, with corresponding changes, to poly-harmonic functions.
. Some other properties of harmonic functions also carry over, with corresponding changes, to poly-harmonic functions.
For poly-harmonic functions of any order 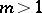 , representations using harmonic functions are generalized to get results known for biharmonic functions [1]–[5]. For example, for a poly-harmonic function
, representations using harmonic functions are generalized to get results known for biharmonic functions [1]–[5]. For example, for a poly-harmonic function  of two variables there is the representation
of two variables there is the representation
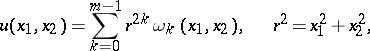 |
where 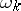 ,
, 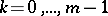 , are harmonic functions in
, are harmonic functions in 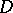 . For a function
. For a function 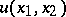 of two variables to be a poly-harmonic function, it is necessary and sufficient that it be the real (or imaginary) part of a poly-analytic function.
of two variables to be a poly-harmonic function, it is necessary and sufficient that it be the real (or imaginary) part of a poly-analytic function.
The basic boundary value problem for a poly-harmonic function of order 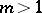 is as follows: Find a poly-harmonic function
is as follows: Find a poly-harmonic function 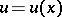 in a region
in a region 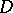 that is continuous along with its derivatives up to and including the order
that is continuous along with its derivatives up to and including the order 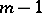 in the closed region
in the closed region 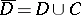 and which satisfies the following conditions on the boundary
and which satisfies the following conditions on the boundary 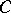 :
:
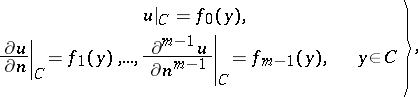 | (*) |
where 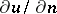 is the derivative along the normal to
is the derivative along the normal to 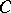 and
and  are given sufficiently smooth functions on the sufficiently smooth boundary
are given sufficiently smooth functions on the sufficiently smooth boundary 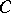 . Many studies deal with solving problem (*) in the ball in
. Many studies deal with solving problem (*) in the ball in 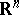 [1], [6]. To solve the problem (*) in the case of an arbitrary region, one uses methods of integral equations, as well as variational methods [1], [6].
[1], [6]. To solve the problem (*) in the case of an arbitrary region, one uses methods of integral equations, as well as variational methods [1], [6].
References
| [1] | I.N. Vekua, "New methods for solving elliptic equations" , North-Holland (1967) (Translated from Russian) |
| [2] | I.I. Privalov, B.M. Pchelin, "Sur la théorie générale des fonctions polyharmoniques" C.R. Acad. Sci. Paris , 204 (1937) pp. 328–330 Mat. Sb. , 2 : 4 (1937) pp. 745–758 |
| [3] | M. Nicolesco, "Les fonctions poly-harmoniques" , Hermann (1936) |
| [4] | M. Nicolesco, "Nouvelles recherches sur les fonctions polyharmoniques" Disq. Math. Phys. , 1 (1940) pp. 43–56 |
| [5] | C. Tolotti, "Sulla struttura delle funzioni iperarmoniche in pui variabili independenti" Giorn. Math. Battaglini , 1 (1947) pp. 61–117 |
| [6] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
Comments
See [a1] for an updated bibliography and for a slightly more general definition:  is poly-harmonic on the domain
is poly-harmonic on the domain  if
if 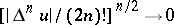 locally uniformly on
locally uniformly on  .
.
References
| [a1] | N. Aronszain, T.M. Creese, L.J. Lipkin, "Polyharmonic functions" , Clarendon Press (1983) |
| [a2] | P.R. Garabedian, "Partial differential equations" , Chelsea, reprint (1986) |
Poly-harmonic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poly-harmonic_function&oldid=12716