Difference between revisions of "Poincaré equations"
Ulf Rehmann (talk | contribs) m (moved Poincaré equations to Poincare equations: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Poincare equations to Poincaré equations over redirect: accented title) |
(No difference)
| |
Revision as of 07:55, 26 March 2012
General equations of the mechanics of holonomic systems (cf. Holonomic system) presented with the help of a certain Lie algebra of infinitesimal transformations.
Let 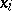 ,
, 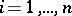 , be variables determining the position of a holonomic mechanical system constrained by ideal constraints depending explicitly on time. If the system has
, be variables determining the position of a holonomic mechanical system constrained by ideal constraints depending explicitly on time. If the system has 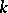 degrees of freedom, then there is an intransitive algebra of infinitesimal transformations
degrees of freedom, then there is an intransitive algebra of infinitesimal transformations
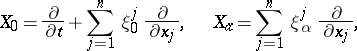 |
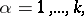 |
enabling the system to be carried at the moment of time 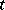 from the position
from the position 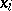 to the infinitesimally-near actual position
to the infinitesimally-near actual position 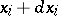 and the virtual position
and the virtual position 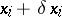 by infinitesimal transformations
by infinitesimal transformations 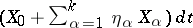 of the algebra and
of the algebra and 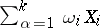 of the subalgebra, respectively. Here
of the subalgebra, respectively. Here 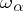 and
and 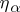 , the independent variables determining the virtual and actual displacements respectively, are connected by the equations
, the independent variables determining the virtual and actual displacements respectively, are connected by the equations
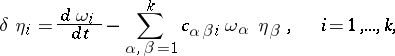 |
if the algebra of virtual displacements 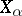 is determined by its structure constants
is determined by its structure constants 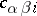 :
:
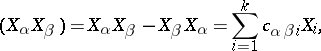 |
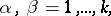 |
and the operator 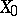 commutes with the algebra of virtual displacements
commutes with the algebra of virtual displacements
 |
Below these conditions are assumed to hold.
The Poincaré equations are ordinary first-order (with respect to 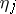 ) differential equations
) differential equations
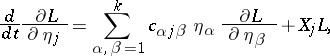 | (1) |
where 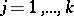 ,
,
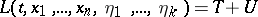 |
is the Lagrange function, 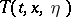 is the kinetic energy and
is the kinetic energy and 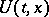 is the force function.
is the force function.
The equations (1) were first obtained by H. Poincaré (see [1]) in the case when the algebra of virtual displacements is transitive and the constraints do not depend explicitly on time, and he applied them (see [2]) to investigate the motion of a solid body with an ellipsoidal cavity, entirely filled by a uniformly vortex moving ideal fluid. N.G. Chetaev (see [3]) generalized and developed the theory of the Poincaré equations to the case where the algebra of displacements is intransitive and the constraints depend explicitly on time (see [3]–[5]) and also converted them to a simpler canonical form (see Chetaev equations). In particular, he gave (see [5]) a method for constructing the algebra of virtual and actual displacements when the holonomic constraints are given by a differential form and he introduced the important concept of cyclic displacements.
Displacements 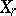 ,
, 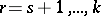 , are said to be cyclic if they satisfy the conditions: 1)
, are said to be cyclic if they satisfy the conditions: 1) 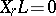 ; 2)
; 2) 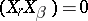 ,
, 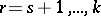 ,
, 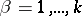 .
.
According to 2) the cyclic displacements 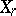 form an Abelian subalgebra of the algebra of virtual displacements which commutes with all the operators
form an Abelian subalgebra of the algebra of virtual displacements which commutes with all the operators 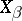 . For cyclic displacements the first integrals of the Poincaré equations,
. For cyclic displacements the first integrals of the Poincaré equations,
 |
exist. From these relations the variables 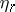 can be expressed in terms of the constants
can be expressed in terms of the constants 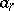 and the variables
and the variables 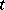 ,
, 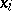 ,
, 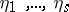 , and one can introduce the Routh function
, and one can introduce the Routh function
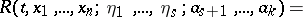 |
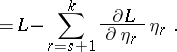 |
Then for the non-cyclic displacements the Poincaré equations take the form
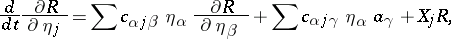 | (2) |
 |
After integrating the equations (2) the values 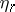 are determined by the equations
are determined by the equations
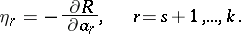 |
If, in addition, 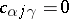 ,
, 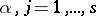 ,
, 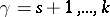 , that is, if the non-cyclic displacements
, that is, if the non-cyclic displacements 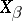 ,
, 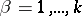 , form a subalgebra of the algebra of virtual displacements, then the mechanical system corresponding to this subalgebra forms some sort of independent holonomic system with
, form a subalgebra of the algebra of virtual displacements, then the mechanical system corresponding to this subalgebra forms some sort of independent holonomic system with  degrees of freedom, described by the equations (1) when
degrees of freedom, described by the equations (1) when 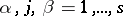 , where the role of the function
, where the role of the function 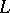 is played by the function
is played by the function 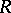 .
.
The Poincaré equations contain as particular cases: the Lagrange equations (in mechanics) when the transformation algebra of infinitesimal increments in one of the variables reduces to a commutative algebra of transformations; and the Euler equation for the rotation of a solid body, when the 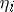 are taken to be the projections
are taken to be the projections 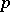 ,
, 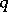 and
and  of the instantaneous angular velocity.
of the instantaneous angular velocity.
References
| [1] | H. Poincaré, C.R. Acad. Sci. Paris , 132 (1901) pp. 369–371 |
| [2] | H. Poincaré, Bull. Astron. , 27 (1910) pp. 321–356 |
| [3] | N.G. Chetaev, Dokl. Akad. Nauk SSSR , 7 (1928) pp. 103–104 |
| [4] | N.G. Chetaev, "Sur les équations de Poincaré" C.R. Acad. Sci. Paris , 185 (1927) pp. 1577–1578 |
| [5] | N.G. Chetaev, Prikl. Mat. i. Mekh. , 5 : 2 (1941) pp. 253–262 |
Poincaré equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poincar%C3%A9_equations&oldid=22925