Pi-solvable group
A generalization of the concept of a solvable group. Let 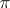 be a certain set of prime numbers. A finite group for which the order of each composition factor either is coprime to any member of
be a certain set of prime numbers. A finite group for which the order of each composition factor either is coprime to any member of 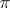 or coincides with a certain prime in
or coincides with a certain prime in 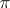 , is called a
, is called a 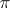 -solvable group. The basic properties of
-solvable group. The basic properties of 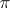 -solvable groups are similar to the properties of solvable groups. A
-solvable groups are similar to the properties of solvable groups. A 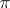 -solvable group is a
-solvable group is a  -solvable group for any
-solvable group for any 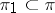 ; the subgroups, quotient groups and extensions of a
; the subgroups, quotient groups and extensions of a 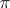 -solvable group by a
-solvable group by a 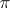 -solvable group are also
-solvable group are also 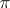 -solvable groups. In a
-solvable groups. In a 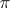 -solvable group
-solvable group 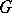 every
every 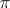 -subgroup (that is, a subgroup all prime factors of the order of which belong to
-subgroup (that is, a subgroup all prime factors of the order of which belong to 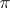 ) is contained in some Hall
) is contained in some Hall 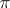 -subgroup (a Hall
-subgroup (a Hall 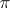 -subgroup is one with index in the group not divisible by any prime in
-subgroup is one with index in the group not divisible by any prime in 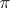 ) and every
) and every  -subgroup (where
-subgroup (where  is the complement of
is the complement of 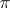 in the set of all prime numbers) is contained in some Hall
in the set of all prime numbers) is contained in some Hall  -subgroup; all Hall
-subgroup; all Hall 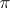 -subgroups and also all Hall
-subgroups and also all Hall  -subgroups are conjugate in
-subgroups are conjugate in  ; the index of a maximal subgroup of the group
; the index of a maximal subgroup of the group  is either not divisible by any number in
is either not divisible by any number in  or is a power of one of the numbers of the set
or is a power of one of the numbers of the set 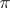 (see [1]). The number of Hall
(see [1]). The number of Hall 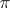 -subgroup in
-subgroup in 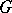 is equal to
is equal to 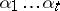 , where
, where 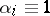 (
(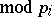 ) for every
) for every 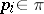 which divides the order of
which divides the order of  , and, moreover,
, and, moreover,  divides the order of one of the chief factors of
divides the order of one of the chief factors of  (see [2]).
(see [2]).
References
| [1] | S.A. Chunikhin, "Subgroups of finite groups" , Wolters-Noordhoff (1969) (Translated from Russian) |
| [2] | W. Brauer, "Zu den Sylowsätzen von Hall und Čunichin" Arch. Math. , 19 : 3 (1968) pp. 245–255 |
Comments
References
| [a1] | D.J.S. Robinson, "A course in the theory of groups" , Springer (1982) |
Pi-solvable group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pi-solvable_group&oldid=15840