Perturbation theory
A group of methods for studying various problems employed in many branches of mathematics, mechanics, physics, and technology. In this article the principal ideas of perturbation theory are given from a general point of view.
Perturbation theory is based on the fact that it is possible to give an approximate description of the system under study using some specially selected "ideal" system which can be correctly and completely studied. One of the criteria of applicability of some part of perturbation theory, depending on the nature of the problem being studied, is that the equations describing the process in question contain a small parameter (or several small parameters), explicitly or implicitly. The requirement is furthermore that if the small parameter is zero, the equation is exactly solvable, so that the problem is reduced to finding the asymptotic behaviour of the best approximation to the true solution, accurately to within 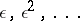 .
.
1) Perturbation theory was first proposed for the solution of problems in celestial mechanics, in the context of the motions of planets in the solar system. Since the planets are very remote from each other, and since their mass is small as compared to the mass of the Sun, the gravitational forces between the planets can be neglected, and the planetary motion is considered, to a first approximation, as taking place along Kepler's orbits, which are defined by the equations of the two-body problem, the two bodies being the planet and the Sun.
Since astronomic data came to be known with much greater accuracy, it became necessary to consider how the motion of a planet around the Sun is affected by other planets. This was the origin of the three-body problem; thus, in studying the system Moon–Earth–Sun the mass ratio between the Moon and the Earth was chosen as the small parameter. J.L. Lagrange and P. Laplace were the first to advance the view that the constants which describe the motion of a planet around the Sun are "perturbed" , as it were, by the motion of other planets and vary as a function of time; hence the name "perturbation theory" .
Perturbation theory was investigated by the classical scholars — Laplace, S. Poisson, C.F. Gauss — as a result of which the computations could be performed with a very high accuracy. The discovery of the planet Neptune in 1848 by J. Adams and U. le Verrier, based on the deviations in motion of the planet Uranus, represented a triumph of perturbation theory.
The difficulty initially involved in the development of this particular theory was the fact that the terms of the expansions obtained contained the time 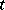 outside the sine or cosine symbol. The contribution of such terms to the series of perturbation theory becomes significant only for long periods of time (of the order of several hundreds of years), but even then only a first approximation rather than accurate planetary motions are obtained. The appearance of the so-called secular terms is due to the dependence of the frequency of the motion (rotation) of the planet under study on the respective frequencies of other planets. If relations of this kind are allowed for, both secular (of the form
outside the sine or cosine symbol. The contribution of such terms to the series of perturbation theory becomes significant only for long periods of time (of the order of several hundreds of years), but even then only a first approximation rather than accurate planetary motions are obtained. The appearance of the so-called secular terms is due to the dependence of the frequency of the motion (rotation) of the planet under study on the respective frequencies of other planets. If relations of this kind are allowed for, both secular (of the form 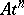 ) and mixed (of the form
) and mixed (of the form 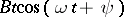 ) terms in fact appear in the solutions. Thus, in the framework of perturbation theory the relation
) terms in fact appear in the solutions. Thus, in the framework of perturbation theory the relation
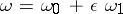 | (1) |
permits the following expansion with respect to  (
(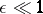 ):
):
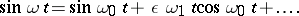 | (2) |
The mixed term in this equation is obtained by expanding oscillations of frequency (1) by oscillations with frequency 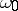 .
.
The development of special methods in perturbation theory, which eliminate the secular terms, i.e. which permit one to obtain the solution in purely trigonometric form, is due to the work of Lindstedt, P. Guldin, Ch. Delaunay, B. Bohlin, and S. Newcomb. The expansion of the frequencies effected by these workers is no longer an expansion by small parameters, i.e. such expansions no longer involve zero-approximation frequencies, but rather by frequencies which have been to some extent redefined or, in modern physical parlance, renormalized. As a result, each member of the power series in perturbation theory by powers of a small parameter is a convergent expression. The problem of the convergence of series in perturbation theory as a whole still remains open, owing to the appearance of the so-called small denominators (small divisors), owing to which the integration of the series to any approximation yields expressions of the type 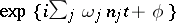 , where
, where 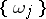 are the frequencies corresponding to the various types of motion. If the frequencies are almost-commensurable, the sum appearing in the exponent may be small, as a result of which the appropriate integration yields series whose terms have small denominators, leading to divergence of the series. In particular, if the ratio between two frequencies
are the frequencies corresponding to the various types of motion. If the frequencies are almost-commensurable, the sum appearing in the exponent may be small, as a result of which the appropriate integration yields series whose terms have small denominators, leading to divergence of the series. In particular, if the ratio between two frequencies 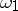 and
and 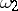 is an irrational number, it is possible to select
is an irrational number, it is possible to select 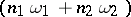 so that the corresponding series in perturbation theory is divergent.
so that the corresponding series in perturbation theory is divergent.
As a result of their study on the problem of small denominators from the point of view of general mathematics, H. Poincaré and A.M. Lyapunov proposed a method for constructing a special kind of periodic solutions which is effective not only in problems of celestial mechanics, but also in the theory of differential equations in general.
They made a substantial contribution to the solution of the problem of small denominators, [4], [5] and [6]. The method of successive canonical change of variables makes it possible to "reduce" the order of the perturbation and to take advantage of the better convergence (so-called super-convergence) to "overcome" the divergence of the series in perturbation theory caused by the appearance of small denominators in each such series of whatever order, by a suitable selection of the canonical transformation.
2) In the perturbation theory of celestial mechanics the asymptotic integration of differential equations was developed for conservative systems only. Subsequent advances in perturbation theory are connected with the development of the theory of oscillations, especially with the development of the theory of non-linear oscillations.
An important role was played by the work of B. van der Pol on Rayleigh-type equations with a small parameter  , which was carried out as a continuation of the work of Lagrange:
, which was carried out as a continuation of the work of Lagrange:
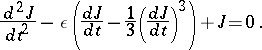 | (3) |
The van der Pol equation is a special case of equation (3).
In order to solve the equation
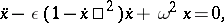 | (4) |
van der Pol proposed to employ (without an adequate mathematical justification) the method of "slowly varying coefficients" , resembling the method used as far back as Lagrange in problems of celestial mechanics. The method involves a representation of equation (4) by harmonically oscillating functions whose amplitudes and phases are slowly varying functions of the parameter 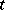 .
.
The general theory of non-linear oscillations was developed by N.M. Krylov and N.N. Bogolyubov. In so doing they overcame basic mathematical difficulties and extended the theory of perturbations to general non-conservative systems. New asymptotic methods of non-linear mechanics, developed in these studies, make it possible to obtain better approximations to solutions by methods of perturbation theory which have a solid mathematical base; in addition, not only a rigorous treatment of periodic solutions but also of quasi-periodic solutions was obtained.
To illustrate the idea of the asymptotic methods of Krylov–Bogolyubov in perturbation theory (cf. also Krylov–Bogolyubov method of averaging), consider the equation
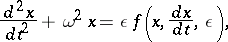 | (5) |
which describes non-linear oscillations of a system with one degree of freedom.
Physical ideas as to the nature of oscillatory processes may be taken as the starting point for a correct formulation of the asymptotic method. Thus, if there is complete linearity, i.e. if 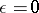 , the oscillations described by equation (5) will be purely harmonic, with a constant amplitude and a uniformly recurring phase. If
, the oscillations described by equation (5) will be purely harmonic, with a constant amplitude and a uniformly recurring phase. If 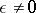 , i.e. if a non-linear perturbation is present, it is natural to expect that the solution of equation (5) will involve overtones, dependence of instantaneous frequency on the amplitude and, finally, a systematic increase or decrease of the amplitude of oscillation, owing to the input or output of energy due to the perturbing forces.
, i.e. if a non-linear perturbation is present, it is natural to expect that the solution of equation (5) will involve overtones, dependence of instantaneous frequency on the amplitude and, finally, a systematic increase or decrease of the amplitude of oscillation, owing to the input or output of energy due to the perturbing forces.
In view of all these physical ideas it is natural to look for a solution of equation (5) as a series
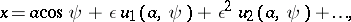 | (6) |
where 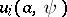 ,
, 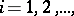 are periodic functions of the angle
are periodic functions of the angle 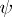 with a period of
with a period of 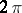 , while the values of
, while the values of  and
and 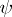 as functions of time are defined by the differential equations
as functions of time are defined by the differential equations
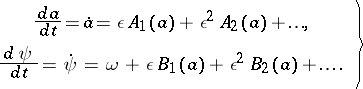 | (7) |
Thus, the problem is reduced to the choice of suitable expressions for the functions 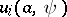 ,
, 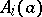 ,
, 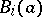 ,
,  so that expression (6), with
so that expression (6), with  and
and 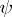 replaced by time-dependent functions as defined by (7), is the solution of the original equation (5). Certain additional conditions are also imposed, in order to prevent the appearance of secular terms in the solution (6).
replaced by time-dependent functions as defined by (7), is the solution of the original equation (5). Certain additional conditions are also imposed, in order to prevent the appearance of secular terms in the solution (6).
If in the formal series (6) the expansion is cut-off after the first few terms, one obtains the 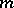 -th approximation; it is asymptotic in the sense that if
-th approximation; it is asymptotic in the sense that if 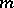 is fixed and
is fixed and 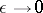 , expression (6) approximates the exact solution of equation (5); the first approximation equations are identical with the van der Pol equation. Estimation of the error involved in the
, expression (6) approximates the exact solution of equation (5); the first approximation equations are identical with the van der Pol equation. Estimation of the error involved in the 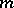 -th approximation presents no special difficulties. The solution of the problem in the case of
-th approximation presents no special difficulties. The solution of the problem in the case of 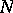 degrees of freedom is carried out in a similar manner.
degrees of freedom is carried out in a similar manner.
If formula (6) is interpreted as a formula of change of variables, rather than as a solution of equation (5), exact expressions may be obtained for the derivatives of the amplitude  and the phase
and the phase 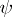 as functions of time.
as functions of time.
It is known [8], [9] that differential equations describing oscillatory processes and containing a "small" parameter may often be reduced to a so-called standard form
 | (8) |
where  is a small positive parameter. A large number of problems in physics and technology can in fact be reduced to this form. A special method of approximation, known as the averaging method, has been developed for systems of differential equations such as (8). According to this method, if the values of
is a small positive parameter. A large number of problems in physics and technology can in fact be reduced to this form. A special method of approximation, known as the averaging method, has been developed for systems of differential equations such as (8). According to this method, if the values of  on a finite interval are sufficiently small, the change of variables
on a finite interval are sufficiently small, the change of variables
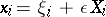 |
can be used to obtain the averaged equations
 |
where
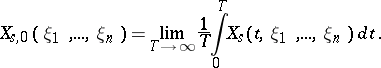 |
The averaging method may be used, for example, to obtain a number of criteria for the existence and the stability of auto-oscillatory systems.
Estimates of the difference 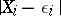 over a time interval of length
over a time interval of length  have been given [13]. It is also possible to check the applicability of such solutions to general systems, which depend on their behaviour on an infinite interval. Theorems on the existence and stability of quasi-periodic solutions have been demonstrated in this way.
have been given [13]. It is also possible to check the applicability of such solutions to general systems, which depend on their behaviour on an infinite interval. Theorems on the existence and stability of quasi-periodic solutions have been demonstrated in this way.
3) In the study of non-linear oscillatory systems it is possible to omit the reduction of the relevant system of equations to "standard form" , and to work instead directly with the initial differential equations for the system of harmonic oscillators subjected to a weak non-linear action. In addition to the general solutions of such systems, it is also possible to obtain partial solutions by appropriately changing variables.
This was in fact the approach adopted by Bogolyubov to certain problems in statistical mechanics, connected with the computation of the distribution functions of  particles (
particles (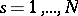 ) for systems of a large number of interacting particles. Both the small constant of interaction and the small density of the particles in the system may be used as the small parameter in problems of statistical mechanics. In one such approximation, higher
) for systems of a large number of interacting particles. Both the small constant of interaction and the small density of the particles in the system may be used as the small parameter in problems of statistical mechanics. In one such approximation, higher  -particle distribution functions may be expressed as the distribution functions of a single particle. Even in the first approximation in perturbation theory it is possible to obtain from the system of kinetic equations the well-known Boltzmann equations, as well as the Landau, Vlasov and Bogolyubov–Lienard–Balescu equations, which are widely employed in plasma theory (cf. e.g. Bogolyubov chain of equations; Boltzmann equation; Vlasov kinetic equation).
-particle distribution functions may be expressed as the distribution functions of a single particle. Even in the first approximation in perturbation theory it is possible to obtain from the system of kinetic equations the well-known Boltzmann equations, as well as the Landau, Vlasov and Bogolyubov–Lienard–Balescu equations, which are widely employed in plasma theory (cf. e.g. Bogolyubov chain of equations; Boltzmann equation; Vlasov kinetic equation).
It should be noted that these methods were developed for applications to equations with a small parameter in their regular part (not as coefficient of the highest derivative). However, the van der Pol equation in the Rayleigh form, for example, is automatically reduced for large values of  to an equation in which the small parameter is the coefficient of the highest derivative. Powerful methods of study have been developed for problems of this kind, where a special approach is required [14], [15], [16], [17].
to an equation in which the small parameter is the coefficient of the highest derivative. Powerful methods of study have been developed for problems of this kind, where a special approach is required [14], [15], [16], [17].
It is precisely the problems with a small parameter as coefficient of the highest derivative which are typical of the problems of statistical mechanics and hydrodynamics. An example is the Navier–Stokes equations applied to small coefficients of viscosity and thermal conduction, for which the zero-th approximation is constituted by Euler's equations for an ideal fluid. This renders the search for the best approximation more complicated in this case.
4) The methods of perturbation theory have special importance in the field of quantum mechanics in which, just like in classical mechanics, exact solutions are obtained for the case of the two-body problem only (which can be reduced to the one-body problem in an external potential field). Two forms of perturbation theory are employed in such a case: one for stationary states, the other for the computation of the probability of transition from one stationary state to another, in the framework of scattering theory. In quantum mechanics, perturbation theory is formulated as a problem on the eigen values for a linear self-adjoint operator of the form
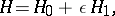 |
where  is a small parameter and where the solution of the problem of the eigen values of the "non-perturbed" operator
is a small parameter and where the solution of the problem of the eigen values of the "non-perturbed" operator 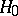 is known, i.e. a complete system of eigen functions
is known, i.e. a complete system of eigen functions 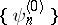 and of eigen values
and of eigen values 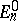 is known, and the spectrum of the operator
is known, and the spectrum of the operator 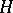 is to be found.
is to be found.
Assuming that  is small, the wave functions
is small, the wave functions
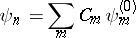 |
and the eigen values  of the energy may be found in the form of series
of the energy may be found in the form of series
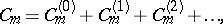 |
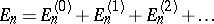 |
in powers of the perturbation  . Perturbation theory then yields the following result for the perturbation of the
. Perturbation theory then yields the following result for the perturbation of the  -th state:
-th state:
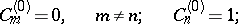 |
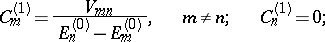 |
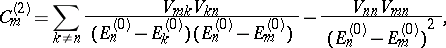 |
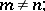 |
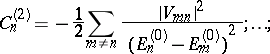 |
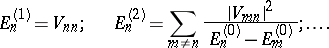 |
Here 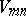 is the matrix element of the perturbation operator defined according to the rule
is the matrix element of the perturbation operator defined according to the rule 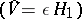 :
:
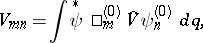 |
where 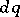 is the volume element.
is the volume element.
The condition of applicability of perturbation theory to such problems,
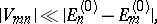 |
is not met if the energy level of the non-perturbed system is degenerate: To a degenerate energy level 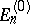 correspond
correspond  states
states 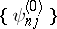 ,
, 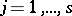 , where
, where  is the multiplicity of the degeneration. In such a case perturbation theory must be applied in a modified form: In the first stage the effect of the perturbation on the degeneration of the state is considered, while the effect of the other levels is regarded as a small perturbation; linear combinations of the
is the multiplicity of the degeneration. In such a case perturbation theory must be applied in a modified form: In the first stage the effect of the perturbation on the degeneration of the state is considered, while the effect of the other levels is regarded as a small perturbation; linear combinations of the  functions of the degenerate state are constructed, and the coefficients
functions of the degenerate state are constructed, and the coefficients 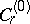 of the combination should satisfy
of the combination should satisfy
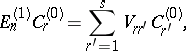 | (9) |
where
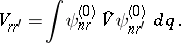 |
The correction of the energy 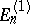 is found from the secular equation of system (9). The solutions
is found from the secular equation of system (9). The solutions 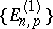 ,
, 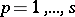 , of this
, of this  -th degree equation are substituted in (9) and
-th degree equation are substituted in (9) and 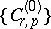 is found, as well as the wave function
is found, as well as the wave function
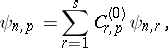 |
which corresponds to the energy
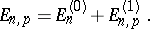 |
Corrections of the next order are found by ordinary methods of perturbation theory.
In the non-stationary case the problem of perturbation theory is posed in terms of the probability of transition from a state 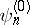 to a state
to a state 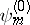 . Perturbation theory may be used in the Heisenberg picture, in the Schrödinger picture or in the interaction picture.
. Perturbation theory may be used in the Heisenberg picture, in the Schrödinger picture or in the interaction picture.
Quantum mechanics also deals with problems of an altogether different type — viz. how to find the so-called scattering matrix of two or more particles. Such problems are particularly important in quantum electrodynamics, which involves a small parameter — the fine structure constant.
The problem of calculating transition probabilities is reduced to the study of a Hamiltonian of the type
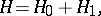 |
where 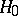 is a free Hamiltonian, while
is a free Hamiltonian, while  is an interaction Hamiltonian.
is an interaction Hamiltonian.
In the Schrödinger picture the form of the equation is
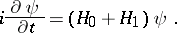 |
By the change of variables
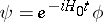 |
it is possible to obtain the following equation for the state 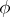 :
:
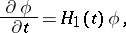 |
where
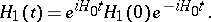 |
The connection between the initial states 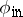 , which describe the "entering" particles, and the final states
, which describe the "entering" particles, and the final states  which describe the "leaving" particles, may be formulated in terms of the so-called scattering operator
which describe the "leaving" particles, may be formulated in terms of the so-called scattering operator 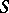 , which is defined by the relationship:
, which is defined by the relationship:
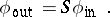 |
It is possible to formally obtain the solution of equation
by the method of successive approximation, in the form of a power series in the interaction:
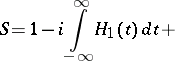 |
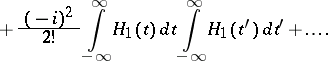 |
In quantum field theory a similar formula is valid, in which 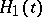 is replaced by the corresponding Lagrange density, and the
is replaced by the corresponding Lagrange density, and the 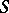 -operator is expressed via a
-operator is expressed via a  -product:
-product:
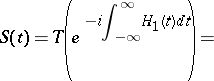 |
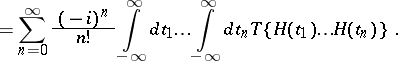 |
The action of the operator 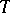 of chronological ordering is defined by the rules:
of chronological ordering is defined by the rules:
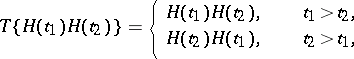 |
this  -product not being formally defined for identical arguments. In order to overcome difficulties of this kind, which appear in the method of perturbation theory when applied to quantum field theory, special regularization methods have been developed. The relativistic invariance of perturbation theory is used to compute the so-called
-product not being formally defined for identical arguments. In order to overcome difficulties of this kind, which appear in the method of perturbation theory when applied to quantum field theory, special regularization methods have been developed. The relativistic invariance of perturbation theory is used to compute the so-called  -matrix, whose entries define the probabilities of transition between the quantum states.
-matrix, whose entries define the probabilities of transition between the quantum states.
References
| [1a] | H. Poincaré, "Les méthodes nouvelles de la mécanique céleste" , 1–3 , Gauthier-Villars (1892–1899) |
| [1b] | H. Poincaré, , Oeuvres de H. Poincaré , 1–3 , Gauthier-Villars (1916–1965) |
| [2] | C. Charlier, "Die Mechanik des Himmels" , 1–3 , de Gruyter (1927) |
| [3] | G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927) |
| [4] | A.N. Kolmogorov, "On dynamic systems with an integral invariant on a torus" Dokl. Akad. Nauk SSSR , 93 : 5 (1953) pp. 763–766 (In Russian) |
| [5] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
| [6] | J.K. Moser, "Lectures on Hamiltonian systems" , Amer. Math. Soc. (1968) |
| [7] | N.N. Bogolyubov, N.M. Krylov, "Méthodes approchées de la mécanique non-linéaire dans leur application à l'Aeetude de la perturbation des mouvements périodiques et de divers phénomènes de résonance s'y rapportant" , Acad. Sci. Ukraine (1935) |
| [8] | N.N. [N.N. Bogolyubov] Bogoliuboff, N.M. [N.M. Krylov] Kryloff, "Introduction to non-linear mechanics" , Kraus (1970) (Translated from Russian) |
| [9] | N.N. Bogolyubov, Yu.A. Mitropol'skii, "Asymptotic methods in the theory of non-linear oscillations" , Hindushtan Publ. Comp. , Delhi (1961) (Translated from Russian) |
| [10] | N.N. Moiseev, "Asymptotic methods of non-linear mechanics" , Moscow (1969) (In Russian) |
| [11] | V.N. Chelomei, "On the possibility of increasing stability of elastic systems by vibrations" Dokl. Akad. Nauk SSSR , 110 : 3 (1956) pp. 345–347 (In Russian) |
| [12] | N.N. [N.N. Bogolyubov] Bogoliubov, Yu.A. [Yu.A. Mitropol'skii] Mitropoliskii, A.M. [A.M. Samoilenko] Samolenko, "Methods of accelerated convergence in non-linear mechanics" , Springer (1976) (Translated from Russian) |
| [13] | N.N. Bogolyubov, "On some statistical methods in mathematical physics" , Kiev (1945) (In Russian) |
| [14] | A.A. Dorodnitsyn, "Asymptotic solution of the van der Pol equation" Priklad. Mat. Mekh. , 11 (1947) pp. 313–328 (In Russian) (English abstract) |
| [15] | A.N. Tikhonov, "On dependence of solutions of differential systems on a small parameter" Mat. Sb. , 22 (64) : 2 pp. 193–204 (In Russian) |
| [16] | L.S. Pontryagin, "Asymptotic behaviour of solutions of a system of differential equations with small parameter in front of the highest derivative" Izv. Akad. Nauk SSSR Ser. Mat. , 21 (1957) pp. 605–626 (In Russian) |
| [17] | E.F. Mishchenko, "Asymptotic calculation of periodic solutions of systems of differential equations with a small parameter in front of the derivatives" Izv. Akad. Nauk SSSR Ser. Mat. , 21 (1957) pp. 627–654 (In Russian) |
| [18] | D.I. Blokhintsev, "Grundlagen der Quantenmechanik" , Deutsch. Verlag Wissenschaft. (953) (Translated from Russian) |
| [19] | N.N. Bogolyubov, "Lectures on quantum statistics" , Gordon & Breach (1967) (Translated from Russian) |
| [20] | N.N. Bogolyubov, "Selected works" , 2 , Kiev (1970) (In Russian) |
| [21] | N.N. Bogolyubov, D.V. Shirkov, "Introduction to the theory of quantized fields" , Interscience (1959) (Translated from Russian) |
| [22] | N.N. Bogolyubov, A.A. Logunov, I.T. Todorov, "Introduction to axiomatic quantum field theory" , Benjamin (1975) (Translated from Russian) |
| [23] | A.I. Akhiezer, V.B. Berestetskii, "Quantenelektrodynamik" , H. Deutsch , Frankfurt a.M. (1962) (Translated from Russian) |
| [24] | V.P. Maslov, "Théorie des perturbations et méthodes asymptotiques" , Dunod (1972) (Translated from Russian) |
Comments
This article describes some topics from the huge area of perturbation methods.
Section 1) is on the classical Poincaré–Lindstedt method for constructing perioding solutions, and touches upon the Kolmogorov–Arnol'd–Moser theory (KAM theory), cf. Quasi-periodic motion and [4]–[6]. A modern tutorial text on there matters is [a6].
Section 2) is on asymptotic methods, originated by van der Pol, Krylov, Bogolyubov and Mitropolskii. However, much has happened in this domain since the original applications. For a modern view one should consult [a7].
Section 3) mentions miscellaneous subjects, among which, very briefly, the large domain of singular perturbations. There are two main classes of problems in that domain: relaxation oscillations [a8] and boundary layer problems [a9].
Singular perturbations.
A singular perturbation is a term or component in a differential equation existing of a derivative term (the highest order in the equation) with a small coefficient  .
.
Many systems of differential equations possess solutions with smooth or non-smooth behaviour according to various time scales. In a particular time scale some may be considered to be slow (i.e. the first few derivatives are relatively small in norm) and others may be viewed as fast (i.e. the derivatives are relatively large in norm). Well-known examples of such systems are ordinary differential equations describing electrical circuits or chemical reactions; in the latter case, e.g., the time scales can be directly related to the reaction rates involved. Quite often these problems can be modelled as a multi-deck system in which the time scale ratios are expressed by (small) parameters. Such a system has the form
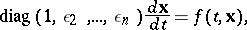 |
with 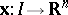 ,
, 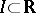 , and
, and  small but positive constants. A particular instance of such a differential equation is the scalar ordinary differential equation
small but positive constants. A particular instance of such a differential equation is the scalar ordinary differential equation
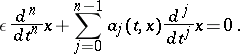 |
It is sufficiently general to consider the two-deck system
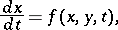 |
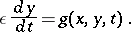 |
For this ordinary differential equation two initial (or boundary) conditions should be prescribed. Of particular interest then is the behaviour of the solution  when
when 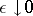 . To avoid confusion, the
. To avoid confusion, the  dependence of this solution is indicated by a superscript
dependence of this solution is indicated by a superscript  . By setting
. By setting 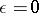 , one obtains the so-called reduced equation. If
, one obtains the so-called reduced equation. If 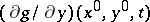 is non-singular in a relevant domain, then one may formally solve for
is non-singular in a relevant domain, then one may formally solve for 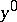 and obtain a first-order ordinary differential equation in
and obtain a first-order ordinary differential equation in 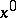 only. Clearly one then needs just one initial (or boundary) condition, so that in general the solution of the reduced problem will not satisfy the other initial or boundary condition. This then explains the name singular perturbation, as convergence of
only. Clearly one then needs just one initial (or boundary) condition, so that in general the solution of the reduced problem will not satisfy the other initial or boundary condition. This then explains the name singular perturbation, as convergence of 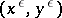 to
to 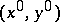 is not uniform at all, cf. [a5]. Given the reduced solution, however, one can relate
is not uniform at all, cf. [a5]. Given the reduced solution, however, one can relate 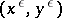 to
to 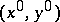 by trying to find a fast solution component moving from the given initial or boundary data to an integral curve "close" to
by trying to find a fast solution component moving from the given initial or boundary data to an integral curve "close" to 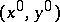 . This is often referred to as a boundary-layer effect, noticeable in an
. This is often referred to as a boundary-layer effect, noticeable in an  -neighbourhood (or
-neighbourhood (or  -related at least) of that initial or boundary point. The above-described usage of the reduced solution is employed by some analytic techniques. Here the reduced solution (called outer solution) is corrected in the layer by a transient solution (inner solution), using power series expansions inside and outside the layer. To make these components approximate the desired solution one has to match them. Therefore this technique is referred to as matched asymptotic expansions.
-related at least) of that initial or boundary point. The above-described usage of the reduced solution is employed by some analytic techniques. Here the reduced solution (called outer solution) is corrected in the layer by a transient solution (inner solution), using power series expansions inside and outside the layer. To make these components approximate the desired solution one has to match them. Therefore this technique is referred to as matched asymptotic expansions.
Layers or transients may not only occur at the boundaries but also in the interior. This is a well-known phenomenon in gas dynamics, where shocks (see Shock waves, mathematical theory of) can often be described as internal layers of such problems. As an example, consider the shock formulation of the viscous Burgers equation
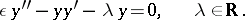 |
One should note that the first derivative term is multiplied by a factor that may become zero. If 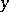 is going through zero, the linearized form of this equation has an eigen value that switches from very large negative to very large positive, or vice versa. Such problems are referred to as turning-point problems, cf. [a4] for a linear theory treatment.
is going through zero, the linearized form of this equation has an eigen value that switches from very large negative to very large positive, or vice versa. Such problems are referred to as turning-point problems, cf. [a4] for a linear theory treatment.
References
| [a1] | D.R. Smith, "Singular perturbation theory" , Cambridge Univ. Press (1985) |
| [a2] | W. Eckhaus, "Matched asymptotic expansion and singular perturbations" , North-Holland (1973) |
| [a3] | R.E. O'Malley jr., "Introduction to singular perturbations" , Acad. Press (1974) |
| [a4] | W. Wasow, "Linear turning point theory" , Springer (1985) |
| [a5] | A.B. Vasil'eva, "Asymptotic behaviour of solutions to certain problems involving nonlinear differential equations containing a small parameter multiplying the highest derivatives" Russian Math. Surveys , 18 : 3 (1963) pp. 13–84 Uspekhi Mat. Nauk , 18 : 3 (1963) pp. 15–86 |
| [a6] | F. Verhulst, "Nonlinear differential equations and dynamical systems" , Springer (1989) |
| [a7] | J.A. Sanders, F. Verhulst, "Averaging methods in nonlinear dynamical systems" , Springer (1985) |
| [a8] | J. Grasman, "Asymptotic methods for relaxation oscillations and applications" , Springer (1987) |
| [a9] | W. Eckhaus, "Asymptotic analysis of singular perturbations" , North-Holland (1979) |
| [a10] | V.I. Arnol'd, A. Avez, "Problèmes ergodiques de la mécanique classique" , Gauthier-Villars (1967) (Translated from Russian) |
| [a11] | R. Bellman, "Perturbation techniques in mathematics, physics and engineering" , Holt, Rinehart & Winston (1964) |
Perturbation theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perturbation_theory&oldid=11676