Difference between revisions of "Permanent"
(Importing text file) |
(cf Immanant) |
||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722503.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722503.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722504.png" /> are elements from a commutative ring and summation is over all one-to-one mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722505.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722506.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722507.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722508.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722509.png" /> represents all possible permutations, and the permanent is a particular case of the Schur matrix function | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722504.png" /> are elements from a commutative ring and summation is over all one-to-one mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722505.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722506.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722507.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722508.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p0722509.png" /> represents all possible permutations, and the permanent is a particular case of the Schur matrix function (cf. [[Immanant]]) |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p07225010.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072250/p07225010.png" /></td> </tr></table> | ||
Revision as of 10:07, 30 November 2014
of an 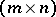 -matrix
-matrix 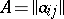
The function
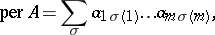 |
where 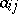 are elements from a commutative ring and summation is over all one-to-one mappings
are elements from a commutative ring and summation is over all one-to-one mappings 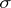 from
from 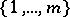 into
into 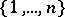 . If
. If  , then
, then 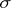 represents all possible permutations, and the permanent is a particular case of the Schur matrix function (cf. Immanant)
represents all possible permutations, and the permanent is a particular case of the Schur matrix function (cf. Immanant)
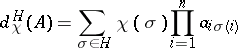 |
for 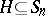 , where
, where 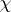 is a character of degree 1 on the subgroup
is a character of degree 1 on the subgroup 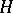 (cf. Character of a group) of the symmetric group
(cf. Character of a group) of the symmetric group 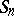 (one obtains the determinant for
(one obtains the determinant for 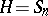 ,
, 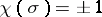 , in accordance with the parity of
, in accordance with the parity of 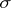 ).
).
The permanent is used in linear algebra, probability theory and combinatorics. In combinatorics, a permanent can be interpreted as follows: The number of systems of distinct repesentatives for a given family of subsets of a finite set is the permanent of the incidence matrix for the incidence system related to this family.
The main interest is in the permanent of a matrix consisting of zeros and ones (a 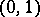 -matrix), of a matrix containing non-negative real numbers, in particular doubly-stochastic matrices (in which the sum of the elements in any row and any column is 1), and of a complex Hermitian matrix. The basic properties of the permanent include a theorem on expansion (the analogue of Laplace's theorem for determinants) and the Binet–Cauchy theorem, which gives a representation of the permanent of the product of two matrices as the sum of the products of the permanents formed from the cofactors. For the permanents of complex matrices it is convenient to use representations as scalar products in the symmetry classes of completely-symmetric tensors (see, e.g., [3]). One of the most effective methods for calculating permanents is provided by Ryser's formula:
-matrix), of a matrix containing non-negative real numbers, in particular doubly-stochastic matrices (in which the sum of the elements in any row and any column is 1), and of a complex Hermitian matrix. The basic properties of the permanent include a theorem on expansion (the analogue of Laplace's theorem for determinants) and the Binet–Cauchy theorem, which gives a representation of the permanent of the product of two matrices as the sum of the products of the permanents formed from the cofactors. For the permanents of complex matrices it is convenient to use representations as scalar products in the symmetry classes of completely-symmetric tensors (see, e.g., [3]). One of the most effective methods for calculating permanents is provided by Ryser's formula:
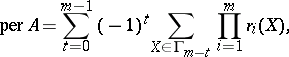 |
where 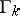 is the set of submatrices of dimension
is the set of submatrices of dimension 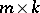 for the square matrix
for the square matrix  ,
, 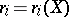 is the sum of the elements of the
is the sum of the elements of the 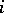 -th row of
-th row of 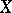 and
and 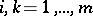 . As it is complicated to calculate permanents, estimating them is important. Some lower bounds are given below.
. As it is complicated to calculate permanents, estimating them is important. Some lower bounds are given below.
a) If 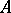 is a
is a 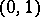 -matrix with
-matrix with  ,
, 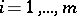 , then
, then
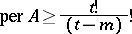 |
for 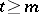 , and
, and
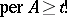 |
if 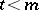 and
and 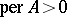 .
.
b) If 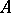 is a
is a 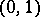 -matrix of order
-matrix of order  , then
, then
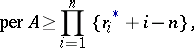 |
where 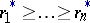 are the sums of the elements in the rows of
are the sums of the elements in the rows of 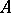 arranged in non-increasing order and
arranged in non-increasing order and 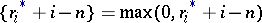 .
.
c) If 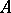 is a positive semi-definite Hermitian matrix of order
is a positive semi-definite Hermitian matrix of order  , then
, then
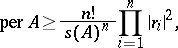 |
where 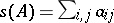 if
if 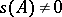 .
.
Upper bounds for permanents:
1) For a 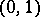 -matrix
-matrix 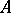 of order
of order  ,
,
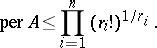 |
2) For a completely-indecomposable matrix 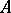 of order
of order  with non-negative integer elements,
with non-negative integer elements,
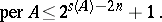 |
3) For a complex normal matrix 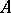 with eigen values
with eigen values 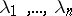 ,
,
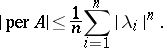 |
The most familiar problem in the theory of permanents was van der Waerden's conjecture: The permanent of a doubly-stochastic matrix of order  is bounded from below by
is bounded from below by 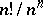 , and this value is attained only for the matrix composed of fractions
, and this value is attained only for the matrix composed of fractions 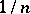 . A positive solution to this problem was obtained in [4].
. A positive solution to this problem was obtained in [4].
Among the applications of permanents one may mention relationships to certain combinatorial problems (cf. Combinatorial analysis), such as the "problème des rencontresproblème de rencontres" and the "problème d'attachementproblème d'attachement" (or "hook problemhook problem" ), and also to the Fibonacci numbers, the enumeration of Latin squares (cf. Latin square) and Steiner triple systems (cf. Steiner system), and to the derivation of the number of 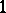 -factors and linear subgraphs of a graph, while doubly-stochastic matrices are related to certain probability models. There are interesting physical applications of permanents, of which the most important is the dimer problem, which arises in research on the adsorption of di-atomic molecules in surface layers: The permanent of a
-factors and linear subgraphs of a graph, while doubly-stochastic matrices are related to certain probability models. There are interesting physical applications of permanents, of which the most important is the dimer problem, which arises in research on the adsorption of di-atomic molecules in surface layers: The permanent of a  -matrix of a simple structure expresses the number of ways of combining the atoms in the substance into di-atomic molecules. There are also applications of permanents in statistical physics, the theory of crystals and physical chemistry.
-matrix of a simple structure expresses the number of ways of combining the atoms in the substance into di-atomic molecules. There are also applications of permanents in statistical physics, the theory of crystals and physical chemistry.
References
| [1] | H.J. Ryser, "Combinatorial mathematics" , Wiley & Math. Assoc. Amer. (1963) |
| [2] | V.N. Sachkov, "Combinatorial methods in discrete mathematics" , Moscow (1977) (In Russian) |
| [3] | H. Minc, "Permanents" , Addison-Wesley (1978) |
| [4] | G.P. Egorichev, "The solution of van der Waerden's problem on permanents" , Krasnoyarsk (1980) (In Russian) |
| [5] | D.I. Falikman, "Proof of the van der Waerden conjecture regarding the permanent of a doubly stochastic matrix" Math. Notes , 29 : 6 (1981) pp. 475–479 Mat. Zametki , 29 : 6 (1981) pp. 931–938 |
Comments
For the upper bound given in 1) see [a7]. For the enumeration of Steiner triple systems see [a6].
The solution of the van der Waerden conjecture was obtained simultaneously and independently of each other in 1979 by both O.I. Falikman, [5], and G.P. Egorichev, [4], [a4]. For some details cf. also [a2]–[a5].
References
| [a1] | D.E. Knuth, "A permanent inequality" Amer. Math. Monthly , 88 (1981) pp. 731–740 |
| [a2] | J.C. Lagarias, "The van der Waerden conjecture: two Soviet solutions" Notices Amer. Math. Soc. , 29 : 2 (1982) pp. 130–133 |
| [a3] | J.H. van Lint, "Notes on Egoritsjev's proof of the van der Waerden conjecture" Linear Algebra Appl. , 39 (1981) pp. 1–8 |
| [a4] | G.P. [G.P. Egorichev] Egorychev, "The solution of van der Waerden's problem for permanents" Adv. in Math. , 42 : 3 (1981) pp. 299–305 |
| [a5] | J.H. van Lint, "The van der Waerden conjecture: Two proofs in one year" Math. Intelligencer , 4 (1982) pp. 72–77 |
| [a6] | R.M. Wilson, "Non-isomorphic triple systems" Math. Zeitschr. , 135 (1974) pp. 303–313 |
| [a7] | A. Schrijver, "A short proof of Minc's conjecture" J. Comb. Theory (A) , 25 (1978) pp. 80–83 |
| [a8] | H. Minc, "Nonnegative matrices" , Wiley (1988) |
Permanent. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Permanent&oldid=18654