Parametrix method
One of the methods for studying boundary value problems for differential equations with variable coefficients by means of integral equations.
Suppose that in some region  of the
of the  -dimensional Euclidean space
-dimensional Euclidean space  one considers an elliptic differential operator (cf. Elliptic partial differential equation) of order
one considers an elliptic differential operator (cf. Elliptic partial differential equation) of order  ,
,
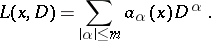 | (1) |
In (1) the symbol  is a multi-index,
is a multi-index,  , where the
, where the  are non-negative integers,
are non-negative integers,  ,
,  ,
, 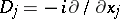 . With every operator (1) there is associated the homogeneous elliptic operator
. With every operator (1) there is associated the homogeneous elliptic operator
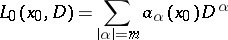 |
with constant coefficients, where  is an arbitrary fixed point. Let
is an arbitrary fixed point. Let  denote a fundamental solution of
denote a fundamental solution of 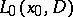 depending parametrically on
depending parametrically on  . Then the function
. Then the function  is called the parametrix of the operator (1) with a singularity at
is called the parametrix of the operator (1) with a singularity at 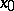 .
.
In particular, for the second-order elliptic operator
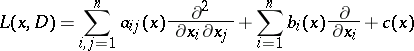 |
one can take as parametrix with singularity at 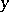 the Levi function
the Levi function
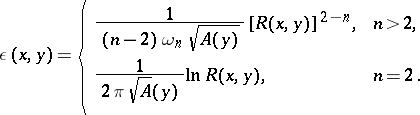 | (2) |
In (2),  ,
,  is the determinant of the matrix
is the determinant of the matrix  ,
,
 |
and  are the elements of the matrix inverse to
are the elements of the matrix inverse to  .
.
Let  be the integral operator
be the integral operator
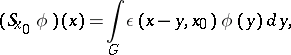 | (3) |
acting on functions from  and let
and let
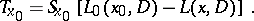 |
Since, by definition of a fundamental solution,
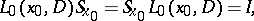 |
where 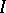 is the identity operator, one has
is the identity operator, one has
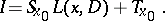 |
This equality indicates that for every sufficiently-smooth function 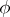 of compact support in
of compact support in  there is a representation
there is a representation
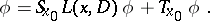 | (4) |
Moreover, if
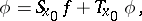 |
then 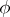 is a solution of the equation
is a solution of the equation
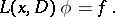 |
Thus, the question of the local solvability of 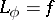 reduces to that of invertibility of
reduces to that of invertibility of 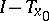 .
.
If one applies  to functions
to functions  that vanish outside a ball of radius
that vanish outside a ball of radius  with centre at
with centre at  , then for a sufficiently small
, then for a sufficiently small  the norm of
the norm of  can be made smaller than one. Then the operator
can be made smaller than one. Then the operator 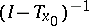 exists; consequently, also
exists; consequently, also  exists, which is the inverse operator to
exists, which is the inverse operator to 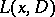 . Here
. Here 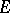 is an integral operator with as kernel a fundamental solution of
is an integral operator with as kernel a fundamental solution of 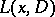 .
.
The name parametrix is sometimes given not only to the function 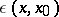 , but also to the integral operator
, but also to the integral operator  with the kernel
with the kernel 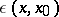 , as defined by (3).
, as defined by (3).
In the theory of pseudo-differential operators, instead of 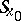 a parametrix of
a parametrix of  is defined as an operator
is defined as an operator 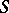 such that
such that  and
and 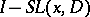 are integral operators with infinitely-differentiable kernels (cf. Pseudo-differential operator). If only
are integral operators with infinitely-differentiable kernels (cf. Pseudo-differential operator). If only 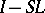 (or
(or 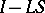 ) is such an operator, then
) is such an operator, then 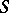 is called a left (or right) parametrix of
is called a left (or right) parametrix of 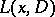 . In other words,
. In other words, 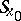 in (4) is a left parametrix if
in (4) is a left parametrix if  in this equality has an infinitely-differentiable kernel. If
in this equality has an infinitely-differentiable kernel. If 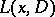 has a left parametrix
has a left parametrix 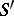 and a right parametrix
and a right parametrix  , then each of them is a parametrix. The existence of a parametrix has been proved for hypo-elliptic pseudo-differential operators (see [3]).
, then each of them is a parametrix. The existence of a parametrix has been proved for hypo-elliptic pseudo-differential operators (see [3]).
References
| [1] | L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964) |
| [2] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [3] | L. Hörmander, , Pseudo-differential operators , Moscow (1967) (In Russian; translated from English) |
Comments
The operator  is called the principal part of
is called the principal part of 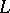 , cf. Principal part of a differential operator. The parametrix method was anticipated in two fundamental papers by E.E. Levi [a1], [a2]. The same procedure is also applicable for constructing the fundamental solution of a parabolic equation with variable coefficients (see, e.g., [a3]).
, cf. Principal part of a differential operator. The parametrix method was anticipated in two fundamental papers by E.E. Levi [a1], [a2]. The same procedure is also applicable for constructing the fundamental solution of a parabolic equation with variable coefficients (see, e.g., [a3]).
References
| [a1] | E.E. Levi, "Sulle equazioni lineari alle derivate parziali totalmente ellittiche" Rend. R. Acc. Lincei, Classe Sci. (V) , 16 (1907) |
| [a2] | E.E. Levi, "Sulle equazioni lineari totalmente ellittiche alle derivate parziali" Rend. Circ. Mat. Palermo , 24 (1907) pp. 275–317 |
| [a3] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
| [a4] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1–4 , Springer (1983–1985) pp. Chapts. 7; 18 |
Parametrix method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parametrix_method&oldid=16020