Difference between revisions of "Papperitz equation"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48101 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
An ordinary second-order Fuchsian linear differential equation having precisely three singular points: | An ordinary second-order Fuchsian linear differential equation having precisely three singular points: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p0711301.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p0711302.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p0711303.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p0711304.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | here | + | here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p0711305.png" /> are pairwise distinct complex numbers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p0711306.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p0711307.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p0711308.png" />) are the characteristic exponents at the singular point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p0711309.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113011.png" />). A Papperitz equation is uniquely determined by the assignment of the singular points and the characteristic exponents. In solving a Papperitz equation (1), use is made of Riemann's notation: |
| − | are pairwise distinct complex numbers, | ||
| − | |||
| − | and | ||
| − | are the characteristic exponents at the singular point | ||
| − | respectively, | ||
| − | and | ||
| − | A Papperitz equation is uniquely determined by the assignment of the singular points and the characteristic exponents. In solving a Papperitz equation (1), use is made of Riemann's notation: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113012.png" /></td> </tr></table> | |
| − | |||
| − | B. Riemann investigated [[#References|[1]]] the problem of finding all many-valued functions | + | B. Riemann investigated [[#References|[1]]] the problem of finding all many-valued functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113013.png" />, analytic in the extended complex plane, which have the following properties: |
| − | analytic in the extended complex plane, which have the following properties: | ||
| − | a) the function | + | a) the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113014.png" /> has precisely three singular points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113015.png" />; |
| − | has precisely three singular points | ||
b) any three of its branches are connected by a linear equation | b) any three of its branches are connected by a linear equation | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113016.png" /></td> </tr></table> | |
| − | |||
| − | |||
with constant coefficients; | with constant coefficients; | ||
| − | c) the function | + | c) the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113017.png" /> has the simplest singularities at the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113018.png" />; namely, in a neighbourhood of the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113019.png" /> there are two branches <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113021.png" /> satisfying |
| − | has the simplest singularities at the points | ||
| − | namely, in a neighbourhood of the point | ||
| − | there are two branches | ||
| − | and | ||
| − | satisfying | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113022.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113023.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113024.png" /> is holomorphic at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113025.png" />; and analogously for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113027.png" />. |
| − | |||
| − | is holomorphic at | ||
| − | and analogously for | ||
| − | and | ||
| − | Riemann, under certain additional assumptions on the numbers | + | Riemann, under certain additional assumptions on the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113028.png" />, showed that all such functions can be expressed in terms of hypergeometric functions and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113029.png" /> satisfies a linear second-order differential equation with rational coefficients, but did not write this equation out explicitly (see [[#References|[1]]]). The equation in question, (1), was given by E. Papperitz [[#References|[2]]]. It is also called the Riemann <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113031.png" />-equation, the Riemann equation in Papperitz's form and the Riemann equation, and its solutions are called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113033.png" />-functions. |
| − | showed that all such functions can be expressed in terms of hypergeometric functions and that | ||
| − | satisfies a linear second-order differential equation with rational coefficients, but did not write this equation out explicitly (see [[#References|[1]]]). The equation in question, (1), was given by E. Papperitz [[#References|[2]]]. It is also called the Riemann | ||
| − | equation, the Riemann equation in Papperitz's form and the Riemann equation, and its solutions are called | ||
| − | functions. | ||
The basic properties of the solutions of a Papperitz equation are as follows. | The basic properties of the solutions of a Papperitz equation are as follows. | ||
| − | 1) A Papperitz equation is invariant under rational-linear transformations: If | + | 1) A Papperitz equation is invariant under rational-linear transformations: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113034.png" /> maps the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113035.png" /> to points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113036.png" />, then |
| − | maps the points | ||
| − | to points | ||
| − | then | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113037.png" /></td> </tr></table> | |
| − | |||
2) The transformation | 2) The transformation | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113038.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
transforms a Papperitz equation into a Papperitz equation with the same singular points, but with different characteristic exponents: | transforms a Papperitz equation into a Papperitz equation with the same singular points, but with different characteristic exponents: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113039.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113040.png" /></td> </tr></table> | |
| − | = | ||
| − | |||
3) The [[Hypergeometric equation|hypergeometric equation]] | 3) The [[Hypergeometric equation|hypergeometric equation]] | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113041.png" /></td> </tr></table> | |
| − | |||
| − | |||
is a special case of a Papperitz equation and it corresponds in Riemann's notation to | is a special case of a Papperitz equation and it corresponds in Riemann's notation to | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113042.png" /></td> </tr></table> | |
| − | |||
4) Each solution of a Papperitz equation can be expressed in terms of the hypergeometric function, | 4) Each solution of a Papperitz equation can be expressed in terms of the hypergeometric function, | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113043.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113044.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | under the assumption that | + | under the assumption that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113045.png" /> is not a negative integer. If none of the differences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113047.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113048.png" /> are integers, then interchanging in (2) the positions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113050.png" /> or of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113051.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113052.png" />, four solutions of a Papperitz equation are obtained. In addition a Papperitz equation remains unchanged if the positions of the triples <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113053.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113054.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113055.png" /> are rearranged; all these rearrangements provide 24 special solutions of a Papperitz equation (1), which were first obtained by E.E. Kummer [[#References|[5]]]. |
| − | is not a negative integer. If none of the differences | ||
| − | |||
| − | |||
| − | are integers, then interchanging in (2) the positions of | ||
| − | and | ||
| − | or of | ||
| − | and | ||
| − | four solutions of a Papperitz equation are obtained. In addition a Papperitz equation remains unchanged if the positions of the triples | ||
| − | |||
| − | |||
| − | are rearranged; all these rearrangements provide 24 special solutions of a Papperitz equation (1), which were first obtained by E.E. Kummer [[#References|[5]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> B. Riemann, "Beiträge zur Theorie der durch Gauss'sche Reihe <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113056.png" /> darstellbare Functionen" , ''Gesammelte math. Werke'' , Dover, reprint (1953) pp. 67–85</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Papperitz, "Ueber verwandte <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113057.png" />-Functionen" ''Math. Ann.'' , '''25''' (1885) pp. 212–221 {{MR|1510304}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 {{MR|1424469}} {{MR|0595076}} {{MR|0178117}} {{MR|1519757}} {{ZBL|0951.30002}} {{ZBL|0108.26903}} {{ZBL|0105.26901}} {{ZBL|53.0180.04}} {{ZBL|47.0190.17}} {{ZBL|45.0433.02}} {{ZBL|33.0390.01}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) {{MR|0100119}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.E. Kummer, "Ueber die hypergeometrische Reihe <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113058.png" />" ''J. Reine Angew. Math.'' , '''15''' (1836) pp. 39–83; 127–172</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B. Riemann, "Beiträge zur Theorie der durch Gauss'sche Reihe <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113056.png" /> darstellbare Functionen" , ''Gesammelte math. Werke'' , Dover, reprint (1953) pp. 67–85</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Papperitz, "Ueber verwandte <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113057.png" />-Functionen" ''Math. Ann.'' , '''25''' (1885) pp. 212–221 {{MR|1510304}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 {{MR|1424469}} {{MR|0595076}} {{MR|0178117}} {{MR|1519757}} {{ZBL|0951.30002}} {{ZBL|0108.26903}} {{ZBL|0105.26901}} {{ZBL|53.0180.04}} {{ZBL|47.0190.17}} {{ZBL|45.0433.02}} {{ZBL|33.0390.01}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) {{MR|0100119}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.E. Kummer, "Ueber die hypergeometrische Reihe <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071130/p07113058.png" />" ''J. Reine Angew. Math.'' , '''15''' (1836) pp. 39–83; 127–172</TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
An ordinary second-order Fuchsian linear differential equation having precisely three singular points:
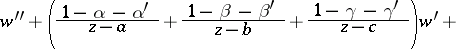 | (1) |
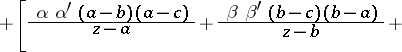 |
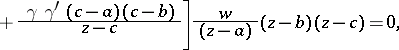 |
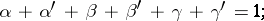 |
here  are pairwise distinct complex numbers,
are pairwise distinct complex numbers,  (
( and
and  ) are the characteristic exponents at the singular point
) are the characteristic exponents at the singular point  (respectively,
(respectively, 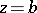 and
and  ). A Papperitz equation is uniquely determined by the assignment of the singular points and the characteristic exponents. In solving a Papperitz equation (1), use is made of Riemann's notation:
). A Papperitz equation is uniquely determined by the assignment of the singular points and the characteristic exponents. In solving a Papperitz equation (1), use is made of Riemann's notation:
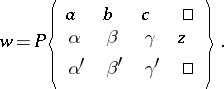 |
B. Riemann investigated [1] the problem of finding all many-valued functions  , analytic in the extended complex plane, which have the following properties:
, analytic in the extended complex plane, which have the following properties:
a) the function 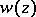 has precisely three singular points
has precisely three singular points 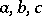 ;
;
b) any three of its branches are connected by a linear equation
 |
with constant coefficients;
c) the function 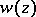 has the simplest singularities at the points
has the simplest singularities at the points  ; namely, in a neighbourhood of the point
; namely, in a neighbourhood of the point  there are two branches
there are two branches 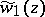 and
and  satisfying
satisfying
 |
where 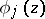
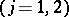 is holomorphic at
is holomorphic at  ; and analogously for
; and analogously for 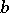 and
and  .
.
Riemann, under certain additional assumptions on the numbers 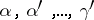 , showed that all such functions can be expressed in terms of hypergeometric functions and that
, showed that all such functions can be expressed in terms of hypergeometric functions and that 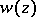 satisfies a linear second-order differential equation with rational coefficients, but did not write this equation out explicitly (see [1]). The equation in question, (1), was given by E. Papperitz [2]. It is also called the Riemann
satisfies a linear second-order differential equation with rational coefficients, but did not write this equation out explicitly (see [1]). The equation in question, (1), was given by E. Papperitz [2]. It is also called the Riemann 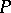 -equation, the Riemann equation in Papperitz's form and the Riemann equation, and its solutions are called
-equation, the Riemann equation in Papperitz's form and the Riemann equation, and its solutions are called 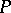 -functions.
-functions.
The basic properties of the solutions of a Papperitz equation are as follows.
1) A Papperitz equation is invariant under rational-linear transformations: If 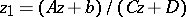 maps the points
maps the points 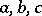 to points
to points 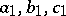 , then
, then
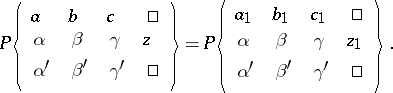 |
2) The transformation
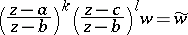 |
transforms a Papperitz equation into a Papperitz equation with the same singular points, but with different characteristic exponents:
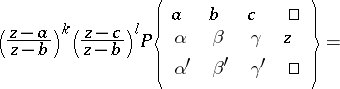 |
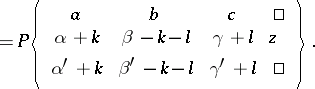 |
3) The hypergeometric equation
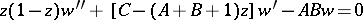 |
is a special case of a Papperitz equation and it corresponds in Riemann's notation to
 |
4) Each solution of a Papperitz equation can be expressed in terms of the hypergeometric function,
 | (2) |
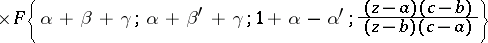 |
under the assumption that 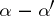 is not a negative integer. If none of the differences
is not a negative integer. If none of the differences 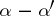 ,
, 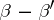 ,
, 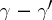 are integers, then interchanging in (2) the positions of
are integers, then interchanging in (2) the positions of  and
and  or of
or of 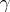 and
and 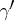 , four solutions of a Papperitz equation are obtained. In addition a Papperitz equation remains unchanged if the positions of the triples
, four solutions of a Papperitz equation are obtained. In addition a Papperitz equation remains unchanged if the positions of the triples  ,
, 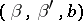 ,
, 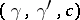 are rearranged; all these rearrangements provide 24 special solutions of a Papperitz equation (1), which were first obtained by E.E. Kummer [5].
are rearranged; all these rearrangements provide 24 special solutions of a Papperitz equation (1), which were first obtained by E.E. Kummer [5].
References
| [1] | B. Riemann, "Beiträge zur Theorie der durch Gauss'sche Reihe 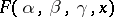 darstellbare Functionen" , Gesammelte math. Werke , Dover, reprint (1953) pp. 67–85 darstellbare Functionen" , Gesammelte math. Werke , Dover, reprint (1953) pp. 67–85 |
| [2] | E. Papperitz, "Ueber verwandte  -Functionen" Math. Ann. , 25 (1885) pp. 212–221 MR1510304 -Functionen" Math. Ann. , 25 (1885) pp. 212–221 MR1510304 |
| [3] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 MR1424469 MR0595076 MR0178117 MR1519757 Zbl 0951.30002 Zbl 0108.26903 Zbl 0105.26901 Zbl 53.0180.04 Zbl 47.0190.17 Zbl 45.0433.02 Zbl 33.0390.01 |
| [4] | V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) MR0100119 |
| [5] | E.E. Kummer, "Ueber die hypergeometrische Reihe  " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 |
Papperitz equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Papperitz_equation&oldid=49352