Paley-Wiener theorem
A function 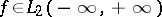 vanishes almost everywhere outside an interval
vanishes almost everywhere outside an interval  if and only if its Fourier transform
if and only if its Fourier transform
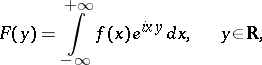 |
satisfies
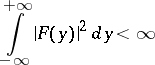 |
and is the restriction to the real line of a certain entire analytic function 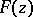 of a complex variable
of a complex variable  satisfying
satisfying  for all
for all  (see [1]). A description of the image of a certain space of functions or generalized functions on a locally compact group under the Fourier transform or under some other injective integral transform is called an analogue of the Paley–Wiener theorem; the most frequently encountered analogues of the Paley–Wiener theorem are a description of the image of the space
(see [1]). A description of the image of a certain space of functions or generalized functions on a locally compact group under the Fourier transform or under some other injective integral transform is called an analogue of the Paley–Wiener theorem; the most frequently encountered analogues of the Paley–Wiener theorem are a description of the image of the space  of infinitely-differentiable functions of compact support and a description of the image of the space
of infinitely-differentiable functions of compact support and a description of the image of the space 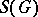 of rapidly-decreasing infinitely-differentiable functions on a locally compact group
of rapidly-decreasing infinitely-differentiable functions on a locally compact group  under the Fourier transform on
under the Fourier transform on 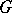 . Such analogues are known, in particular, for Abelian locally compact groups, for certain connected Lie groups, for certain subalgebras of the algebra
. Such analogues are known, in particular, for Abelian locally compact groups, for certain connected Lie groups, for certain subalgebras of the algebra 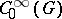 on real semi-simple Lie groups, and also for certain other integral transforms.
on real semi-simple Lie groups, and also for certain other integral transforms.
References
| [1] | N. Wiener, R.E.A.C. Paley, "Fourier transforms in the complex domain" , Amer. Math. Soc. (1934) |
| [2] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1977) (Translated from Russian) |
| [3] | I.M. Gel'fand, M.I. Graev, N.Ya. Vilenkin, "Generalized functions" , 5. Integral geometry and representation theory , Acad. Press (1966) (Translated from Russian) |
| [4] | D.P. Zhelobenko, "Harmonic analysis of functions on semi-simple complex Lie groups" , Moscow (1974) (In Russian) |
| [5] | W. Rudin, "Functional analysis" , McGraw-Hill (1973) |
Comments
Let 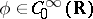 with
with 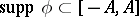 . Then the Fourier transform
. Then the Fourier transform 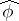 of
of 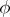 can be extended to an entire analytic function on
can be extended to an entire analytic function on 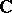 satisfying: for any integer
satisfying: for any integer 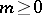 there is a constant
there is a constant 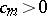 such that for all
such that for all 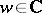 ,
,
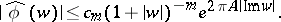 | (*) |
Conversely, let 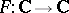 be an entire function which satisfies (*) (replacing
be an entire function which satisfies (*) (replacing 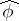 with
with 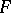 ), for some
), for some 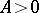 . Then there exists a
. Then there exists a 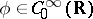 with
with 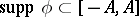 and
and 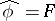 .
.
References
| [a1] | F. Trèves, "Topological vectorspaces, distributions and kernels" , Acad. Press (1967) |
| [a2] | G. Warner, "Harmonic analysis on semi-simple Lie groups" , II , Springer (1972) |
| [a3] | S. Helgason, "Groups and geometric analysis" , Acad. Press (1984) pp. Chapt. II, Sect. 4 |
| [a4] | Y. Katznelson, "An introduction to harmonic analysis" , Dover, reprint (1976) |
Paley-Wiener theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Paley-Wiener_theorem&oldid=22883