P-adic number
An element of an extension of the field of rational numbers (cf. Extension of a field) based on the divisibility of integers by a given prime number 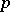 . The extension is obtained by completing the field of rational numbers with respect to a non-Archimedean valuation (cf. Norm on a field).
. The extension is obtained by completing the field of rational numbers with respect to a non-Archimedean valuation (cf. Norm on a field).
A 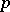 -adic integer, for an arbitrary prime number
-adic integer, for an arbitrary prime number 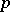 , is a sequence
, is a sequence 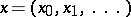 of residues
of residues 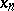 modulo
modulo 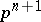 which satisfy the condition
which satisfy the condition
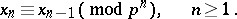 |
The addition and the multiplication of 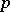 -adic integers is defined by the formulas
-adic integers is defined by the formulas
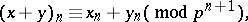 |
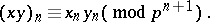 |
Each integer 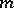 is identified with the
is identified with the 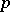 -adic number
-adic number  . With respect to addition and multiplication, the
. With respect to addition and multiplication, the 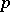 -adic integers form a ring which contains the ring of integers. The ring of
-adic integers form a ring which contains the ring of integers. The ring of 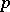 -adic integers may also be defined as the projective limit
-adic integers may also be defined as the projective limit
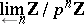 |
of residues modulo 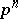 (with respect to the natural projections).
(with respect to the natural projections).
A 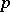 -adic number, or rational
-adic number, or rational 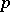 -adic number, is an element of the quotient field
-adic number, is an element of the quotient field  of the ring
of the ring 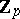 of
of 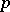 -adic integers. This field is called the field of
-adic integers. This field is called the field of 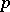 -adic numbers and it contains the field of rational numbers as a subfield. Both the ring and the field of
-adic numbers and it contains the field of rational numbers as a subfield. Both the ring and the field of 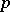 -adic numbers carry a natural topology. This topology may be defined by a metric connected with the
-adic numbers carry a natural topology. This topology may be defined by a metric connected with the 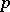 -adic norm, i.e. with the function
-adic norm, i.e. with the function  of the
of the 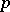 -adic number
-adic number  which is defined as follows. If
which is defined as follows. If 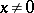 ,
,  can be uniquely represented as
can be uniquely represented as  , where
, where  is an invertible element of the ring of
is an invertible element of the ring of 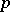 -adic integers. The
-adic integers. The 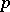 -adic norm
-adic norm 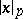 is then equal to
is then equal to  . If
. If 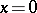 , then
, then 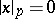 . If
. If 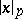 is initially defined on rational numbers only, the field of
is initially defined on rational numbers only, the field of 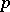 -adic numbers can be obtained as the completion of the field of rational numbers with respect to the
-adic numbers can be obtained as the completion of the field of rational numbers with respect to the 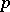 -adic norm.
-adic norm.
Each element of the field of 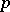 -adic numbers may be represented in the form
-adic numbers may be represented in the form
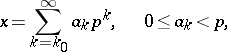 | (*) |
where 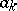 are integers,
are integers, 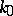 is some integer,
is some integer, 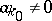 , and the series (*) converges in the metric of the field
, and the series (*) converges in the metric of the field  . The numbers
. The numbers 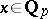 with
with 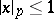 (i.e.
(i.e. 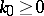 ) form the ring
) form the ring 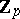 of
of 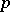 -adic integers, which is the completion of the ring of integers
-adic integers, which is the completion of the ring of integers 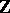 of the field
of the field 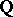 . The numbers
. The numbers 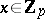 with
with 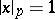 (i.e.
(i.e.  ,
,  ) form a multiplicative group and are called
) form a multiplicative group and are called 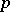 -adic units. The set of numbers
-adic units. The set of numbers 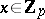 with
with  (i.e.
(i.e. 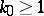 ) forms a principal ideal in
) forms a principal ideal in 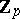 with generating element
with generating element 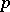 . The ring
. The ring 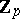 is a complete discrete valuation ring (cf. also Discretely-normed ring). The field
is a complete discrete valuation ring (cf. also Discretely-normed ring). The field 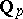 is locally compact in the topology induced by the metric
is locally compact in the topology induced by the metric 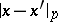 . It therefore admits an invariant measure
. It therefore admits an invariant measure 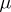 , usually taken with the condition
, usually taken with the condition  . For different
. For different 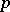 , the valuations
, the valuations 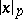 are independent, and the fields
are independent, and the fields 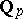 are non-isomorphic. Numerous facts and concepts of classical analysis can be generalized to the case of
are non-isomorphic. Numerous facts and concepts of classical analysis can be generalized to the case of 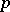 -adic fields.
-adic fields.
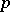 -adic numbers are connected with the solution of Diophantine equations modulo increasing powers of a prime number. Thus, if
-adic numbers are connected with the solution of Diophantine equations modulo increasing powers of a prime number. Thus, if 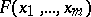 is a polynomial with integral coefficients, the solvability, for all
is a polynomial with integral coefficients, the solvability, for all 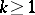 , of the congruence
, of the congruence
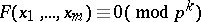 |
is equivalent to the solvability of the equation 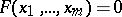 in
in 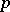 -adic integers. A necessary condition for the solvability of this equation in integers or in rational numbers is its solvability in the rings or, correspondingly, in the fields of
-adic integers. A necessary condition for the solvability of this equation in integers or in rational numbers is its solvability in the rings or, correspondingly, in the fields of 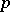 -adic numbers for all
-adic numbers for all 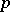 . Such an approach to the solution of Diophantine equations and, in particular, the question whether these conditions — the so-called local conditions — are sufficient, constitutes an important branch of modern number theory (cf. Diophantine geometry).
. Such an approach to the solution of Diophantine equations and, in particular, the question whether these conditions — the so-called local conditions — are sufficient, constitutes an important branch of modern number theory (cf. Diophantine geometry).
The above solvability condition may in one special case be replaced by a simpler one. In fact, if
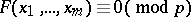 |
has a solution 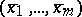 and if this solution defines a non-singular point of the hypersurface
and if this solution defines a non-singular point of the hypersurface 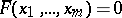 , where
, where 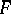 is the polynomial
is the polynomial 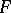 modulo
modulo 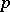 , then this equation has a solution in
, then this equation has a solution in 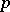 -adic integers which is congruent to
-adic integers which is congruent to 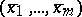 modulo
modulo 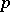 . This theorem, which is known as the Hensel lemma, is a special case of a more general fact in the theory of schemes.
. This theorem, which is known as the Hensel lemma, is a special case of a more general fact in the theory of schemes.
The ring of 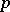 -adic integers may be regarded as a special case of the construction of Witt rings
-adic integers may be regarded as a special case of the construction of Witt rings 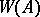 . The ring of
. The ring of 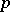 -adic integers is obtained if
-adic integers is obtained if  is the finite field of
is the finite field of 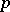 elements (cf. Witt vector). Another generalization of
elements (cf. Witt vector). Another generalization of 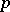 -adic numbers are
-adic numbers are 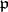 -adic numbers, resulting from the completion of algebraic number fields with respect to non-Archimedean valuations connected with prime divisors.
-adic numbers, resulting from the completion of algebraic number fields with respect to non-Archimedean valuations connected with prime divisors.
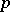 -adic numbers were introduced by K. Hensel [1]. Their canonical representation (*) is analogous to the expansion of analytic functions into power series. This is one of the manifestations of the analogy between algebraic numbers and algebraic functions.
-adic numbers were introduced by K. Hensel [1]. Their canonical representation (*) is analogous to the expansion of analytic functions into power series. This is one of the manifestations of the analogy between algebraic numbers and algebraic functions.
References
| [1] | K. Hensel, "Ueber eine neue Begründung der Theorie der algebraischen Zahlen" Jahresber. Deutsch. Math.-Verein , 6 : 1 (1899) pp. 83–88 |
| [2] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [3] | S. Lang, "Algebraic numbers" , Springer (1986) |
| [4] | H. Weyl, "Algebraic theory of numbers" , Princeton Univ. Press (1959) |
| [5] | H. Hasse, "Zahlentheorie" , Akademie Verlag (1963) |
| [6] | A. Weil, "Basic number theory" , Springer (1974) |
| [7] | N. Bourbaki, "Elements of mathematics" , 7. Commutative algebra , Addison-Wesley (1972) (Translated from French) |
P-adic number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=P-adic_number&oldid=16260