Pólya theorem
Let 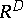 be the set of mappings from a finite set
be the set of mappings from a finite set 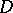 ,
,  , into a set
, into a set 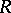 , and let
, and let 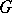 be the permutation group for
be the permutation group for 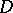 . This group generates a decomposition of
. This group generates a decomposition of 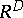 into equivalence classes in which
into equivalence classes in which 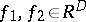 belong to the same class if and only if one can find a
belong to the same class if and only if one can find a 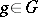 such that
such that 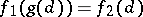 for all
for all 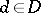 . Assign to each
. Assign to each 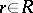 a weight
a weight 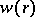 that is an element of a commutative ring. The weight of
that is an element of a commutative ring. The weight of 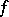 is taken to be equal to
is taken to be equal to 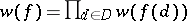 and the weight
and the weight 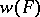 of a class
of a class 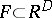 is defined as the weight of any
is defined as the weight of any 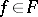 . One then has
. One then has
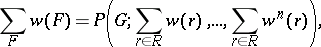 |
where the sum on the left is taken over all the equivalence classes and
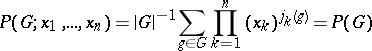 |
is the cycle index of 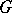 , where
, where 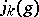 is the number of cycles of length
is the number of cycles of length 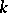 of the permutation
of the permutation 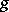 in its decomposition as a product of independent cycles.
in its decomposition as a product of independent cycles.
The theorem was published in 1937 by G. Pólya [3].
If for the weights of the elements of 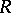 one takes powers of an independent variable
one takes powers of an independent variable  (or the product of powers of several variables), then for
(or the product of powers of several variables), then for 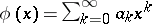 (the so-called "series that enumerates figures" , where
(the so-called "series that enumerates figures" , where 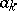 is the number of elements in
is the number of elements in 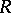 of weight
of weight 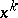 ) and
) and 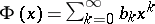 (the so-called "series that enumerates configurations" , where
(the so-called "series that enumerates configurations" , where 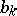 is the number of classes in
is the number of classes in 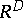 of weight
of weight 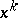 ), the following applies, according to Pólya's theorem:
), the following applies, according to Pólya's theorem:
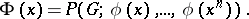 |
Examples.
1) If 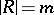 ,
, 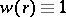 , then
, then 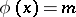 and
and 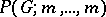 is the number of equivalence classes.
is the number of equivalence classes.
2) If 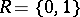 ,
, 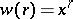 , then
, then 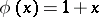 , and
, and 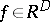 with
with 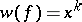 can be interpreted as a subset of
can be interpreted as a subset of 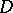 of cardinality
of cardinality 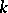 . The group
. The group 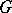 defines orbits of subsets of
defines orbits of subsets of 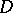 , and the coefficient of
, and the coefficient of 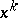 in the polynomial
in the polynomial 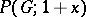 is the number of orbits consisting of subsets of cardinality
is the number of orbits consisting of subsets of cardinality 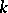 .
.
3) Let 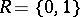 and let
and let 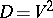 be all
be all  -subsets
-subsets 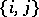 of a set
of a set 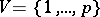 ; then
; then 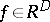 is a labelled graph with vertices from
is a labelled graph with vertices from 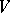 in which the two vertices
in which the two vertices 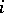 and
and 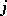 are adjacent if
are adjacent if 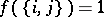 . Let
. Let 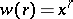 ; then if
; then if 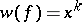 ,
, 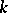 is the number of edges in the graph corresponding to the mapping
is the number of edges in the graph corresponding to the mapping 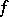 . If the symmetric group
. If the symmetric group 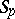 acts on
acts on 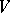 , then on defining for
, then on defining for 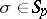 the substitution
the substitution 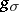 in
in 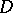 by the relation
by the relation 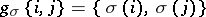 one obtains a binary group
one obtains a binary group 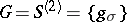 acting on
acting on 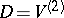 .
.
For the sequence 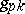 (the numbers of graphs with
(the numbers of graphs with 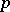 vertices and
vertices and 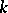 edges),
edges), 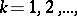 Pólya's theorem gives the generating function
Pólya's theorem gives the generating function
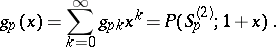 |
For the identity permutation group 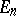 , the symmetric permutation group
, the symmetric permutation group 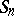 and the binary permutation group
and the binary permutation group 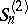 , the cycle index has the form
, the cycle index has the form
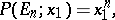 |
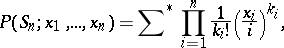 |
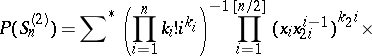 |
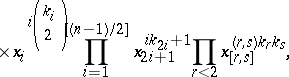 |
respectively, where 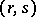 is the greatest common divisor and
is the greatest common divisor and 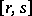 is the least common multiple of
is the least common multiple of  and
and  , and the summation
, and the summation 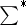 extends over
extends over 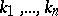 subject to the condition
subject to the condition 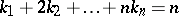 . Cycle indices are known for alternating, cyclic and dihedral groups, as well as formulas for deriving the cycle indices for the product, the Cartesian product and the wreath product of groups [4].
. Cycle indices are known for alternating, cyclic and dihedral groups, as well as formulas for deriving the cycle indices for the product, the Cartesian product and the wreath product of groups [4].
There are extensions of Pólya's theorem to cases of a different definition of the weight function and equivalence classes [1].
References
| [1] | N.G. de Bruijn, "Polya's theory of counting" E.F. Beckenbach (ed.) , Applied combinatorial mathematics , Wiley (1964) pp. Chapt. 5 |
| [2] | V.N. Sachkov, "Combinatorial methods in discrete mathematics" , Moscow (1977) (In Russian) |
| [3] | G. Pólya, "Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen" Acta Math. , 68 (1937) pp. 145–254 |
| [4] | F Harary, E. Palmer, "Graphical enumeration" , Acad. Press (1973) |
Pólya theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=P%C3%B3lya_theorem&oldid=23502