Ordered groupoid
A groupoid  whose elements are partially ordered by a relation
whose elements are partially ordered by a relation  satisfying the axioms
satisfying the axioms
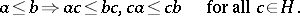 |
If an ordered groupoid  satisfies the stronger axiom
satisfies the stronger axiom
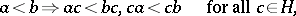 |
then the order on  is called strict, and
is called strict, and  is a strictly partially ordered groupoid. A partially ordered groupoid
is a strictly partially ordered groupoid. A partially ordered groupoid  is said to be strong if
is said to be strong if
 |
A strongly partially ordered groupoid is always strict, and for totally ordered groupoids the two concepts coincide.
An element  of an ordered groupoid
of an ordered groupoid 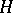 is called positive (strictly positive) if the inequalities
is called positive (strictly positive) if the inequalities  and
and  (respectively,
(respectively, 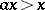 and
and 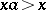 ) hold for all
) hold for all 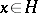 . Negative and strictly negative elements are defined by the opposite inequalities. An ordered groupoid is called positively (negatively) ordered if all its elements are positive (negative). Some special types of ordered groupoids are of particular interest (cf. Naturally ordered groupoid; Ordered semi-group; Ordered group).
. Negative and strictly negative elements are defined by the opposite inequalities. An ordered groupoid is called positively (negatively) ordered if all its elements are positive (negative). Some special types of ordered groupoids are of particular interest (cf. Naturally ordered groupoid; Ordered semi-group; Ordered group).
Comments
The above definition refers to the first of the two meanings of the word groupoid. Groupoids in the second sense also occur naturally with orderings in various contexts: for example, the groupoid of all partial automorphisms of an algebraic or topological structure (that is, isomorphisms between its substructures — e.g. the groupoid of diffeomorphisms between open subsets of a smooth manifold) is naturally ordered by the relation: 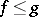 if
if  is the restriction of
is the restriction of  to a subset of its domain. Ordered groupoids of this type are of importance in differential geometry (see [a1]). More generally, any inverse semi-group (cf. Inversion semi-group)
to a subset of its domain. Ordered groupoids of this type are of importance in differential geometry (see [a1]). More generally, any inverse semi-group (cf. Inversion semi-group) 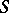 can be regarded as a groupoid, whose objects are the idempotent elements of
can be regarded as a groupoid, whose objects are the idempotent elements of 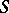 , and where the domain and codomain of an element
, and where the domain and codomain of an element  are
are 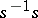 and
and  , respectively; here the objects have a natural meet semi-lattice ordering, and the order can also be defined on morphisms in a natural way (see [a2]).
, respectively; here the objects have a natural meet semi-lattice ordering, and the order can also be defined on morphisms in a natural way (see [a2]).
References
| [a1] | Ch. Ehresmann, "Structures locales et catégories ordonnés" , Oeuvres complètes et commentées , Supplément aux Cahiers de Topologie et Géométrie Différentielle Catégoriques , Partie II (1980) |
| [a2] | J.M. Howie, "An introduction to semigroup theory" , Acad. Press (1976) |
Ordered groupoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ordered_groupoid&oldid=12296