Nuclear bilinear form
A bilinear form  on the Cartesian product
on the Cartesian product  of two locally convex spaces
of two locally convex spaces  and
and  that can be represented as
that can be represented as
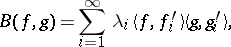 |
where  is a summable sequence,
is a summable sequence,  and
and  are equicontinuous sequences (cf. Equicontinuity) in the dual spaces
are equicontinuous sequences (cf. Equicontinuity) in the dual spaces  and
and  of
of  and
and  , respectively, and
, respectively, and 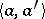 denotes the value of the linear functional
denotes the value of the linear functional  on the vector
on the vector  . All nuclear bilinear forms are continuous. If
. All nuclear bilinear forms are continuous. If 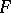 is a nuclear space, then for any locally convex space
is a nuclear space, then for any locally convex space  all continuous bilinear forms on
all continuous bilinear forms on  are nuclear (the kernel theorem). This result is due to A. Grothendieck [1]; the form stated is given in [2]; for other statements see [3]. The converse holds: If a space
are nuclear (the kernel theorem). This result is due to A. Grothendieck [1]; the form stated is given in [2]; for other statements see [3]. The converse holds: If a space  satisfies the kernel theorem, then it is a nuclear space.
satisfies the kernel theorem, then it is a nuclear space.
For spaces of smooth functions of compact support, the kernel theorem was first obtained by L. Schwartz [4]. Let  be the nuclear space of all infinitely-differentiable functions with compact support on the real line, equipped with the standard locally convex topology of Schwartz, so that the dual space
be the nuclear space of all infinitely-differentiable functions with compact support on the real line, equipped with the standard locally convex topology of Schwartz, so that the dual space  consists of all generalized functions on the line. In the special case when
consists of all generalized functions on the line. In the special case when  , the kernel theorem is equivalent to the following assertion: Every continuous bilinear functional on
, the kernel theorem is equivalent to the following assertion: Every continuous bilinear functional on  has the form
has the form
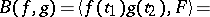 |
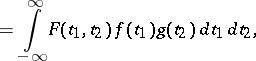 |
where 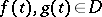 and
and  is a generalized function in two variables. There are similar statements of the kernel theorem for spaces of smooth functions in several variables with compact support, for spaces of rapidly-decreasing functions, and for other specific nuclear spaces. Similar results are valid for multilinear forms.
is a generalized function in two variables. There are similar statements of the kernel theorem for spaces of smooth functions in several variables with compact support, for spaces of rapidly-decreasing functions, and for other specific nuclear spaces. Similar results are valid for multilinear forms.
A continuous bilinear form  on
on  can be identified with a continuous linear operator
can be identified with a continuous linear operator  by using the equality
by using the equality
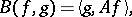 |
and this leads to Schwartz' kernel theorem: For any continuous linear mapping 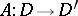 there is a unique generalized function
there is a unique generalized function  such that
such that
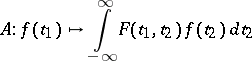 |
for all  . In other words,
. In other words,  is an integral operator with kernel
is an integral operator with kernel 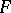 .
.
References
| [1] | A. Grothendieck, "Produits tensoriels topologiques et espaces nucléaires" , Amer. Math. Soc. (1955) |
| [2] | A. Pietsch, "Nuclear locally convex spaces" , Springer (1972) (Translated from German) |
| [3] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1964) (Translated from Russian) |
| [4] | L. Schwartz, "Théorie des noyaux" , Proc. Internat. Congress Mathematicians (Cambridge, 1950) , 1 , Amer. Math. Soc. (1952) pp. 220–230 |
| [5] | L. Schwartz, "Espaces de fonctions différentielles à valeurs vectorielles" J. d'Anal. Math. , 4 (1954–1955) pp. 88–148 |
Comments
References
| [a1] | F. Trèves, "Topological vectorspaces, distributions and kernels" , Acad. Press (1967) |
| [a2] | L. Schwartz, "Théorie des distributions" , 1–2 , Hermann (1966) |
Nuclear bilinear form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nuclear_bilinear_form&oldid=16398