Difference between revisions of "Normal scheme"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48017 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A [[Scheme|scheme]] all local rings (cf. [[Local ring|Local ring]]) of which are normal (that is, reduced and integrally closed in their ring of fractions). A normal scheme is locally irreducible; for such a scheme the concepts of a connected component and an irreducible component are the same. The set of singular points of a Noetherian normal scheme has codimension greater than 1. The following normality criterion holds [[#References|[1]]]: A [[Noetherian scheme|Noetherian scheme]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n0676101.png" /> is normal if and only if two conditions are satisfied: 1) for any point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n0676102.png" /> of codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n0676103.png" /> the local ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n0676104.png" /> is regular (cf. [[Regular ring (in commutative algebra)|Regular ring (in commutative algebra)]]); and 2) for any point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n0676105.png" /> of codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n0676106.png" /> the depth of the ring (cf. [[Depth of a module|Depth of a module]]) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n0676107.png" /> is greater than 1. Every [[Reduced scheme|reduced scheme]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n0676108.png" /> has a normal scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n0676109.png" /> canonically connected with it (normalization). The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761010.png" />-scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761011.png" /> is integral, but not always finite over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761012.png" />. However, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761013.png" /> is excellent (see [[Excellent ring|Excellent ring]]), for example, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761014.png" /> is a scheme of finite type over a field, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761015.png" /> is finite over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761016.png" />. |
| − | n0676101.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | if | ||
| − | |||
| − | {{ | + | ====References==== |
| − | {{ | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.-P. Serre, "Algèbre locale. Multiplicités" , ''Lect. notes in math.'' , '''11''' , Springer (1975) {{MR|0201468}} {{ZBL|0296.13018}} </TD></TR></table> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | A normalization of an irreducible algebraic variety | + | A normalization of an irreducible algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761017.png" /> is an irreducible normal variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761018.png" /> together with a regular mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761019.png" /> that is finite and a birational isomorphism. |
| − | is an irreducible normal variety | ||
| − | together with a regular mapping | ||
| − | that is finite and a birational isomorphism. | ||
| − | For an affine irreducible algebraic variety, | + | For an affine irreducible algebraic variety, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761020.png" /> is the integral closure of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761021.png" /> of regular functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761022.png" /> in its field of fractions. The normalization has the following universality properties. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761023.png" /> be an integral scheme (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761024.png" /> is both reduced and irreducible, or, equivalently, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761025.png" /> is an integral domain for all open <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761026.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761027.png" />). For every normal integral scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761028.png" /> and every dominant morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761029.png" /> (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761030.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761031.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761032.png" /> factors uniquely through the normalization <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761033.png" />. So also [[Normal analytic space|Normal analytic space]]. |
| − | is the integral closure of the ring | ||
| − | of regular functions on | ||
| − | in its field of fractions. The normalization has the following universality properties. Let | ||
| − | be an integral scheme (i.e. | ||
| − | is both reduced and irreducible, or, equivalently, | ||
| − | is an integral domain for all open | ||
| − | in | ||
| − | For every normal integral scheme | ||
| − | and every dominant morphism | ||
| − | i.e. | ||
| − | is dense in | ||
| − | |||
| − | factors uniquely through the normalization | ||
| − | So also [[Normal analytic space|Normal analytic space]]. | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761034.png" /> be a curve and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761035.png" /> a, possibly singular, point on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761036.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761037.png" /> be the normalization of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761038.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761039.png" /> the inverse images of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761040.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761041.png" />. These points are called the branches of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761042.png" /> passing through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761043.png" />. The terminology derives from the fact that the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761044.png" /> can be identified (in the case of varieties over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761045.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761046.png" />) with the "branches" of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761047.png" /> passing through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761048.png" />. More precisely, if the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761049.png" /> are sufficiently small complex or real neighbourhoods of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761050.png" />, then some neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761051.png" /> is the union of the branches <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761052.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761053.png" /> be the tangent space at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761054.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761055.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761056.png" /> is some linear subspace of the tangent space to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761057.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761058.png" />. It will be either a line or a point. In the first case the branch <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761059.png" /> is called linear. The point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761060.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761061.png" /> is an example of a point with two linear branches (with tangents <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761062.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761063.png" />), and the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761064.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761065.png" /> gives an example of a two-fold non-linear branch. |
| − | be a curve and | ||
| − | a, possibly singular, point on | ||
| − | Let | ||
| − | be the normalization of | ||
| − | and | ||
| − | the inverse images of | ||
| − | in | ||
| − | These points are called the branches of | ||
| − | passing through | ||
| − | The terminology derives from the fact that the | ||
| − | can be identified (in the case of varieties over | ||
| − | or | ||
| − | with the "branches" of | ||
| − | passing through | ||
| − | More precisely, if the | ||
| − | are sufficiently small complex or real neighbourhoods of the | ||
| − | then some neighbourhood of | ||
| − | is the union of the branches | ||
| − | Let | ||
| − | be the tangent space at | ||
| − | to | ||
| − | Then | ||
| − | is some linear subspace of the tangent space to | ||
| − | at | ||
| − | It will be either a line or a point. In the first case the branch | ||
| − | is called linear. The point | ||
| − | |||
| − | is an example of a point with two linear branches (with tangents | ||
| − | |||
| − | and the point | ||
| − | |||
| − | gives an example of a two-fold non-linear branch. | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067610/n06761066.png" /></td> </tr></table> | |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1974) pp. Sect. II.5 (Translated from Russian) {{MR|0366917}} {{ZBL|0284.14001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Matsumura, "Commutative algebra" , Benjamin (1970) {{MR|0266911}} {{ZBL|0211.06501}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1974) pp. Sect. II.5 (Translated from Russian) {{MR|0366917}} {{ZBL|0284.14001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Matsumura, "Commutative algebra" , Benjamin (1970) {{MR|0266911}} {{ZBL|0211.06501}} </TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
A scheme all local rings (cf. Local ring) of which are normal (that is, reduced and integrally closed in their ring of fractions). A normal scheme is locally irreducible; for such a scheme the concepts of a connected component and an irreducible component are the same. The set of singular points of a Noetherian normal scheme has codimension greater than 1. The following normality criterion holds [1]: A Noetherian scheme  is normal if and only if two conditions are satisfied: 1) for any point
is normal if and only if two conditions are satisfied: 1) for any point  of codimension
of codimension  the local ring
the local ring  is regular (cf. Regular ring (in commutative algebra)); and 2) for any point
is regular (cf. Regular ring (in commutative algebra)); and 2) for any point  of codimension
of codimension  the depth of the ring (cf. Depth of a module)
the depth of the ring (cf. Depth of a module)  is greater than 1. Every reduced scheme
is greater than 1. Every reduced scheme  has a normal scheme
has a normal scheme  canonically connected with it (normalization). The
canonically connected with it (normalization). The 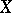 -scheme
-scheme 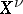 is integral, but not always finite over
is integral, but not always finite over  . However, if
. However, if 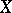 is excellent (see Excellent ring), for example, if
is excellent (see Excellent ring), for example, if 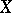 is a scheme of finite type over a field, then
is a scheme of finite type over a field, then 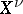 is finite over
is finite over 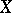 .
.
References
| [1] | J.-P. Serre, "Algèbre locale. Multiplicités" , Lect. notes in math. , 11 , Springer (1975) MR0201468 Zbl 0296.13018 |
Comments
A normalization of an irreducible algebraic variety 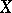 is an irreducible normal variety
is an irreducible normal variety 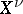 together with a regular mapping
together with a regular mapping 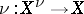 that is finite and a birational isomorphism.
that is finite and a birational isomorphism.
For an affine irreducible algebraic variety, 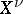 is the integral closure of the ring
is the integral closure of the ring 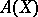 of regular functions on
of regular functions on 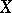 in its field of fractions. The normalization has the following universality properties. Let
in its field of fractions. The normalization has the following universality properties. Let 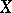 be an integral scheme (i.e.
be an integral scheme (i.e. 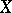 is both reduced and irreducible, or, equivalently,
is both reduced and irreducible, or, equivalently, 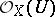 is an integral domain for all open
is an integral domain for all open 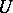 in
in 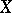 ). For every normal integral scheme
). For every normal integral scheme 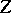 and every dominant morphism
and every dominant morphism 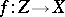 (i.e.
(i.e. 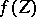 is dense in
is dense in 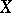 ),
), 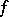 factors uniquely through the normalization
factors uniquely through the normalization 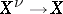 . So also Normal analytic space.
. So also Normal analytic space.
Let 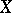 be a curve and
be a curve and  a, possibly singular, point on
a, possibly singular, point on  . Let
. Let 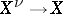 be the normalization of
be the normalization of 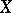 and
and  the inverse images of
the inverse images of  in
in 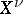 . These points are called the branches of
. These points are called the branches of 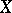 passing through
passing through  . The terminology derives from the fact that the
. The terminology derives from the fact that the 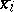 can be identified (in the case of varieties over
can be identified (in the case of varieties over  or
or  ) with the "branches" of
) with the "branches" of 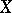 passing through
passing through  . More precisely, if the
. More precisely, if the 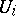 are sufficiently small complex or real neighbourhoods of the
are sufficiently small complex or real neighbourhoods of the 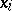 , then some neighbourhood of
, then some neighbourhood of  is the union of the branches
is the union of the branches 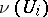 . Let
. Let 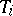 be the tangent space at
be the tangent space at  to
to  . Then
. Then 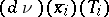 is some linear subspace of the tangent space to
is some linear subspace of the tangent space to  at
at  . It will be either a line or a point. In the first case the branch
. It will be either a line or a point. In the first case the branch 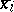 is called linear. The point
is called linear. The point 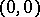 on
on 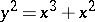 is an example of a point with two linear branches (with tangents
is an example of a point with two linear branches (with tangents  ,
, 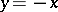 ), and the point
), and the point 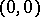 on
on 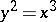 gives an example of a two-fold non-linear branch.
gives an example of a two-fold non-linear branch.
 |
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 MR0463157 Zbl 0367.14001 |
| [a2] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1974) pp. Sect. II.5 (Translated from Russian) MR0366917 Zbl 0284.14001 |
| [a3] | H. Matsumura, "Commutative algebra" , Benjamin (1970) MR0266911 Zbl 0211.06501 |
Normal scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_scheme&oldid=49340