Normal p-complement

of a finite group

A normal subgroup such that and , where is a Sylow -subgroup of (see Sylow subgroup). A group 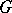has a normal -complement if some Sylow 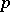-subgroup 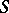of 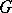lies in the centre of its normalizer (cf. Normalizer of a subset) (Burnside's theorem). A necessary and sufficient condition for the existence of a normal 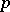-complement in a group 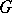is given by Frobenius' theorem: A group has a normal 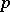-complement if and only either for any non-trivial 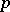-subgroup 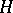of 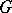the quotient group is a 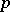-group (where 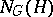is the normalizer and 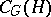the centralizer of in 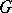) or if for every non-trivial 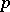-subgroup 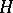of 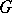the subgroup 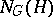has a normal -complement.

References

[1]	D. Gorenstein, "Finite groups" , Harper & Row (1968)

Comments

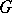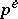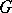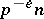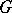Let be a group of order and let be the highest power of a prime number dividing . A subgroup of of index (and hence of order ) is called a -complement in . A normal -complement is a 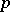-complement that is normal. A finite group is solvable if and only if it has a 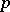-complement for every prime number 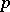dividing its order. Cf. [a1], [a2] for more details; cf. also Hall subgroup.

References

[a1]	M. Hall jr., "The theory of groups" , Macmillan (1959) pp. Sect. 9.3
[a2]	B. Huppert, "Endliche Gruppen" , 1 , Springer (1967) pp. Sect. VI.1