Difference between revisions of "Norm"
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
| + | {{TEX|want}} | ||
A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067340/n0673401.png" /> from a [[Vector space|vector space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067340/n0673402.png" /> over the field of real or complex numbers into the real numbers, subject to the conditions: | A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067340/n0673401.png" /> from a [[Vector space|vector space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067340/n0673402.png" /> over the field of real or complex numbers into the real numbers, subject to the conditions: | ||
Revision as of 17:11, 22 February 2013
A mapping  from a vector space
from a vector space  over the field of real or complex numbers into the real numbers, subject to the conditions:
over the field of real or complex numbers into the real numbers, subject to the conditions:
 , and
, and  for
for  only;
only;
 for every scalar
for every scalar  ;
;
 for all
for all  (the triangle axiom). The number
(the triangle axiom). The number 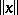 is called the norm of the element
is called the norm of the element  .
.
A vector space 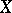 with a distinguished norm is called a normed space. A norm induces on
with a distinguished norm is called a normed space. A norm induces on 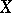 a metric by the formula
a metric by the formula 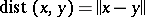 , hence also a topology compatible with this metric. And so a normed space is endowed with the natural structure of a topological vector space. A normed space that is complete in this metric is called a Banach space. Every normed space has a Banach completion.
, hence also a topology compatible with this metric. And so a normed space is endowed with the natural structure of a topological vector space. A normed space that is complete in this metric is called a Banach space. Every normed space has a Banach completion.
A topological vector space is said to be normable if its topology is compatible with some norm. Normability is equivalent to the existence of a convex bounded neighbourhood of zero (a theorem of Kolmogorov, 1934).
The norm in a normed vector space 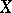 is generated by an inner product (that is,
is generated by an inner product (that is,  is isometrically isomorphic to a pre-Hilbert space) if and only if for all
is isometrically isomorphic to a pre-Hilbert space) if and only if for all 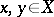 ,
,
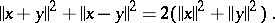 |
Two norms 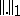 and
and  on one and the same vector space
on one and the same vector space 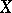 are called equivalent if they induce the same topology. This comes to the same thing as the existence of two constants
are called equivalent if they induce the same topology. This comes to the same thing as the existence of two constants 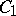 and
and  such that
such that
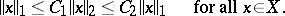 |
If  is complete in both norms, then their equivalence is a consequence of compatibility. Here compatibility means that the limit relations
is complete in both norms, then their equivalence is a consequence of compatibility. Here compatibility means that the limit relations
 |
imply that 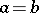 .
.
Not every topological vector space, even if it is assumed to be locally convex, has a continuous norm. For example, there is no continuous norm on an infinite product of straight lines with the topology of coordinate-wise convergence. The absence of a continuous norm can be an obvious obstacle to the continuous imbedding of one topological vector space in another.
If 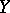 is a closed subspace of a normed space
is a closed subspace of a normed space 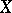 , then the quotient space
, then the quotient space 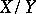 of cosets by
of cosets by 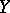 can be endowed with the norm
can be endowed with the norm
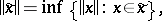 |
under which it becomes a normed space. The norm of the image of an element  under the quotient mapping
under the quotient mapping 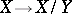 is called the quotient norm of
is called the quotient norm of  with respect to
with respect to 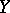 .
.
The totality 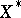 of continuous linear functionals
of continuous linear functionals 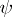 on a normed space
on a normed space 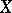 forms a Banach space relative to the norm
forms a Banach space relative to the norm
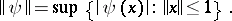 |
The norms of all functionals are attained at suitable points of the unit ball of the original space if and only if the space is reflexive (cf. Reflexive space).
The totality 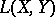 of continuous (bounded) linear operators
of continuous (bounded) linear operators  from a normed space
from a normed space 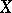 into a normed space
into a normed space 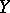 is made into a normed space by introducing the operator norm:
is made into a normed space by introducing the operator norm:
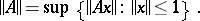 |
Under this norm 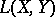 is complete if
is complete if 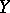 is. When
is. When 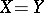 is complete, the space
is complete, the space 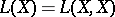 with multiplication (composition) of operators becomes a Banach algebra, since for the operator norm
with multiplication (composition) of operators becomes a Banach algebra, since for the operator norm
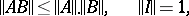 |
where 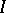 is the identity operator (the unit element of the algebra). Other equivalent norms on
is the identity operator (the unit element of the algebra). Other equivalent norms on 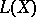 subject to the same condition are also interesting. Such norms are sometimes called algebraic or ringed. Algebraic norms can be obtained by renorming
subject to the same condition are also interesting. Such norms are sometimes called algebraic or ringed. Algebraic norms can be obtained by renorming 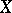 equivalently and taking the corresponding operator norms; however, even for
equivalently and taking the corresponding operator norms; however, even for 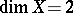 not all algebraic norms on
not all algebraic norms on  can be obtained in this manner.
can be obtained in this manner.
A pre-norm, or semi-norm, on a vector space 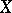 is defined as a mapping
is defined as a mapping 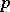 with the properties of a norm except non-degeneracy:
with the properties of a norm except non-degeneracy: 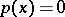 does not preclude that
does not preclude that 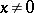 . If
. If 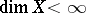 , a non-zero pre-norm
, a non-zero pre-norm 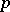 on
on 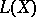 subject to the condition
subject to the condition 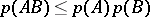 actually turns out to be a norm (since in this case
actually turns out to be a norm (since in this case 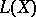 has no non-trivial two-sided ideals). But for infinite-dimensional normed spaces this is not so. If
has no non-trivial two-sided ideals). But for infinite-dimensional normed spaces this is not so. If 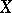 is a Banach algebra over
is a Banach algebra over 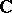 , then the spectral radius
, then the spectral radius
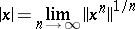 |
is a semi-norm if and only if it is uniformly continuous on  , and this condition is equivalent to the fact that the quotient algebra by the radical is commutative.
, and this condition is equivalent to the fact that the quotient algebra by the radical is commutative.
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [2] | W.I. [V.I. Sobolev] Sobolew, "Elemente der Funktionalanalysis" , H. Deutsch , Frankfurt a.M. (1979) (Translated from Russian) |
| [3] | G.E. Shilov, "Mathematical analysis" , 1–2 , M.I.T. (1974) (Translated from Russian) |
| [4] | L.V. Kantorovich, G.P. Akilov, "Functionalanalysis in normierten Räumen" , Akademie Verlag (1977) (Translated from Russian) |
| [5] | W. Rudin, "Functional analysis" , McGraw-Hill (1979) |
| [6] | M.M. Day, "Normed linear spaces" , Springer (1973) |
| [7] | I.M. Glazman, Yu.I. Lyubich, "Finite-dimensional linear analysis: a systematic presentation in problem form" , M.I.T. (1974) (Translated from Russian) |
| [8] | B. Aupetit, "Propriétés spectrales des algèbres de Banach" , Springer (1979) |
| [9] | A.D. Grishiani, "Theorems and problems in functional analysis" , Springer (1982) (Translated from Russian) |
Comments
The theorem that the norms of all functionals are attained at points of the unit ball of the original space 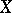 if and only if
if and only if 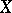 is reflexive is called James' theorem.
is reflexive is called James' theorem.
References
| [a1] | B. Beauzamy, "Introduction to Banach spaces and their geometry" , North-Holland (1982) |
| [a2] | J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces" , 1–2 , Springer (1977–1979) |
For norms in algebra see Norm on a field or ring (see also Valuation).
The norm of a group is the collection of group elements that commute with all subgroups, that is, the intersection of the normalizers of all subgroups (cf. Normalizer of a subset). The norm contains the centre of the group (cf. Centre of a group) and is contained in the second hypercentre 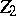 . For groups with a trivial centre the norm is the trivial subgroup
. For groups with a trivial centre the norm is the trivial subgroup 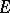 .
.
References
| [1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
O.A. Ivanova
Comments
References
| [a1] | D.J.S. Robinson, "Finiteness conditions and generalized solvable groups" , 2 , Springer (1972) pp. 45 |
Norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Norm&oldid=29469