Difference between revisions of "Noether-Enriques theorem"
Ulf Rehmann (talk | contribs) m (moved Noether–Enriques theorem to Noether-Enriques theorem: ascii title) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Noether, "Ueber invariante Darstellung algebraischer Funktionen" ''Math. Ann.'' , '''17''' (1880) pp. 263–284</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D.W. Babbage, "A note on the quadrics through a canonical curve" ''J. London. Math. Soc.'' , '''14''' : 4 (1939) pp. 310–314</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B. Saint-Donat, "On Petri's analysis of the linear system of quadrics through a canonical curve" ''Mat. Ann.'' , '''206''' (1973) pp. 157–175</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.V. Shokurov, "The Noether–Enriques theorem on canonical curves" ''Math. USSR Sb.'' , '''15''' (1971) pp. 361–403 ''Math. Sb.'' , '''86''' : 3 (1971) pp. 367–408</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E. Arbarello, E. Sernesi, "Petri's approach to the study of the ideal associated to a special divisor" ''Invent. Math.'' , '''49''' (1978) pp. 99–119</TD></TR></table> |
| Line 24: | Line 24: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E. Arbarello, M. Cornalba, P.A. Griffiths, J.E. Harris, "Geometry of algebraic curves" , '''1''' , Springer (1984) {{MR|2807457}} {{MR|0770932}} {{ZBL|05798333}} {{ZBL|0991.14012}} {{ZBL|0559.14017}} </TD></TR></table> |
Revision as of 21:54, 30 March 2012
on canonical curves
A theorem on the projective normality of a canonical curve and on its definability by quadratic equations.
Let  be a smooth canonical (non-hyper-elliptic) curve of genus
be a smooth canonical (non-hyper-elliptic) curve of genus  over an algebraically closed field
over an algebraically closed field  and let
and let  be the homogeneous ideal in the ring
be the homogeneous ideal in the ring  defining
defining  in
in  . The Noether–Enriques theorem (sometimes called the Noether–Enriques–Petri theorem) asserts that:
. The Noether–Enriques theorem (sometimes called the Noether–Enriques–Petri theorem) asserts that:
1)  is projectively normal in
is projectively normal in  ;
;
2) if  , then
, then  is a plane curve of degree 4, and if
is a plane curve of degree 4, and if  , then the graded ideal
, then the graded ideal  is generated by the components of degree 2 and 3 (which means that
is generated by the components of degree 2 and 3 (which means that  is the intersection of the quadrics and cubics in
is the intersection of the quadrics and cubics in  passing through it);
passing through it);
3)  is always generated by the components of degree 2, except when a)
is always generated by the components of degree 2, except when a)  is a trigonal curve, that is, has a linear series (system)
is a trigonal curve, that is, has a linear series (system) 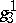 , of dimension 1 and degree 3; or b)
, of dimension 1 and degree 3; or b)  is of genus 6 and is isomorphic to a plane curve of degree 5;
is of genus 6 and is isomorphic to a plane curve of degree 5;
4) in the exceptional cases a) and b) the quadrics passing through  intersect along a surface
intersect along a surface  which for a) is non-singular, rational, ruled of degree
which for a) is non-singular, rational, ruled of degree  in
in 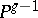 ,
, 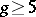 , and the series
, and the series  cuts out on
cuts out on  a linear system of straight lines on
a linear system of straight lines on  , and for
, and for  a quadric in
a quadric in  (possibly a cone); and for b) is the Veronese surface
(possibly a cone); and for b) is the Veronese surface  in
in  .
.
This theorem (in a slightly different algebraic formulation) was established by M. Noether in [1]; a geometric account was given by F. Enriques (on his results see [2]; a modern account is in [3], [4]; a generalization in [5]).
References
| [1] | M. Noether, "Ueber invariante Darstellung algebraischer Funktionen" Math. Ann. , 17 (1880) pp. 263–284 |
| [2] | D.W. Babbage, "A note on the quadrics through a canonical curve" J. London. Math. Soc. , 14 : 4 (1939) pp. 310–314 |
| [3] | B. Saint-Donat, "On Petri's analysis of the linear system of quadrics through a canonical curve" Mat. Ann. , 206 (1973) pp. 157–175 |
| [4] | V.V. Shokurov, "The Noether–Enriques theorem on canonical curves" Math. USSR Sb. , 15 (1971) pp. 361–403 Math. Sb. , 86 : 3 (1971) pp. 367–408 |
| [5] | E. Arbarello, E. Sernesi, "Petri's approach to the study of the ideal associated to a special divisor" Invent. Math. , 49 (1978) pp. 99–119 |
Comments
A smooth curve  is called
is called  -normal if the hypersurfaces of degree
-normal if the hypersurfaces of degree  cut out the complete linear system
cut out the complete linear system  . Instead of
. Instead of  -normal, linearly normal is used. A curve
-normal, linearly normal is used. A curve  is projectively normal if it is
is projectively normal if it is  -normal for every
-normal for every  . Cf. [a2], p. 140ff and 221ff for more details and results.
. Cf. [a2], p. 140ff and 221ff for more details and results.
References
| [a1] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [a2] | E. Arbarello, M. Cornalba, P.A. Griffiths, J.E. Harris, "Geometry of algebraic curves" , 1 , Springer (1984) MR2807457 MR0770932 Zbl 05798333 Zbl 0991.14012 Zbl 0559.14017 |
Noether-Enriques theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Noether-Enriques_theorem&oldid=22851