Nevanlinna theorems
Two fundamental theorems, proved by R. Nevanlinna (see [1], [2]), that are basic for the theory of value distribution of meromorphic functions (see Value-distribution theory). Let $ f ( z) $
be a meromorphic function on a disc
$$ K _ {R} = \{ {z } : {| z | < R \leq \infty } \} , $$
where $ R = \infty $ means that $ f ( z) $ is meromorphic in the entire open complex plane. For every $ r $, $ 0 \leq r < R $, the proximity function of $ f ( z) $ to a number $ a $ is defined by
$$ m ( r, \infty , f ) = \ \frac{1}{2 \pi } \int\limits _ { 0 } ^ { {2 } \pi } \mathop{\rm ln} ^ {+} | f ( re ^ {i \theta } ) | d \theta , $$
$$ m ( r, a, f ) = m \left ( r, \infty , \frac{1}{f - a } \right ) ,\ a \neq \infty , $$
and the counting function of the number of $ a $- points of $ f ( z) $ by
$$ N ( r, a, f ) = \ \int\limits _ { 0 } ^ { r } \frac{n ( t, a, f ) - n ( 0, a, f ) }{t} \ dt + n ( 0, a, f ) \mathop{\rm ln} r, $$
where $ n ( t, a, f ) $ denotes the number of $ a $- points of $ f ( z) $, counting multiplicities, in the disc $ \{ {z } : {| z | \leq t } \} $, i.e. the number of elements of $ f ^ { - 1 } ( a ) \cap \{ {z } : {| z | \leq t } \} $, and $ \mathop{\rm ln} ^ {+} x = \mathop{\rm ln} x $ for $ x \geq 1 $, $ \mathop{\rm ln} ^ {+} x = 0 $ for $ 0 \leq x < 1 $.
The function $ T ( r, f ) = m ( r, \infty , f ) + N ( r, \infty , f ) $ is called the Nevanlinna characteristic of $ f ( z) $.
Nevanlinna's first theorem. For any function $ f ( z) $ that is meromorphic on a disc $ K _ {R} $, for any $ r $, $ 0 \leq r < R $, and any complex number $ a $,
$$ \tag{1 } m ( r, a, f ) + N ( r, a, f ) = T ( r, f ) + \phi ( r, a), $$
where
$$ | \phi ( r, a) | \leq \mathop{\rm ln} ^ {+} | a | + | \mathop{\rm ln} | c | | + \mathop{\rm ln} 2. $$
Here $ c $ denotes the first non-zero coefficient in the Laurent expansion about zero of the function $ f ( z) - a $ if $ f ( 0) = a \neq \infty $, and of $ f ( z) $ itself if $ f ( 0) = \infty $. Thus, for a function whose characteristic $ T ( r, f ) $ increases without limit as $ r \rightarrow R $, the sum $ m ( r, a, f ) + N ( r, a, f ) $, considered for different values of $ a $, is equal to the value $ T ( r, f ) $ up to a bounded additive term $ \phi ( r, a) $. In this sense, all values $ a $ are equivalent for any function $ f ( z) $ that is meromorphic on $ K _ {R} $. For this reason, the theory of value distribution of meromorphic functions concerns itself with questions about the asymptotic behaviour of one term, $ m ( r, a, f ) $ or $ N ( r, a, f ) $, in the invariant sum (1).
Nevanlinna's second theorem shows that, for almost all points $ a $, the principal role in the sum (1) is played by $ N ( r, a, f ) $. The statement of the theorem is as follows.
For any function $ f ( z) $ that is meromorphic on a disc $ K _ {R} = \{ {z } : {| z | < R \leq \infty } \} $, every $ q $, $ q \geq 3 $, and any distinct numbers $ \{ a _ {k} \} _ {k = 1 } ^ {q} $ in the extended complex plane, the relation
$$ \tag{2 } \sum _ {k = 1 } ^ { q } m ( r, a _ {k} , f ) \leq \ 2T ( r, f ) - N _ {1} ( r, f ) + S ( r, f ) $$
holds, where
$$ N _ {1} ( r, f ) = N ( r , \infty , 1 / f ^ { \prime } ) + 2N ( r, \infty , f ) - N ( r, \infty , f ^ { \prime } ), $$
and the term $ S ( r, f ) $ has the following properties:
1) If $ R = \infty $, i.e. if $ f ( z) $ is meromorphic in the entire open complex plane, then
$$ S ( r, f ) = O ( \mathop{\rm ln} ( r \cdot T ( r, f ))), $$
as $ r \rightarrow \infty $, for all values of $ r $ with the possible exception of a set $ E $ of finite total measure.
2) If $ R < \infty $, then
$$ S ( r, f ) = \ O \left ( \mathop{\rm ln} \left ( \frac{R}{R - r } T ( r, f ) \right ) \right ) , $$
as $ r \rightarrow R $, for all values of $ r $ with the possible exception of a set $ E $ for which
$$ \int\limits _ { E } \frac{dr}{R - r } < \infty . $$
The function $ N _ {1} ( r, f ) $ is non-decreasing with increasing $ r $, and therefore the right-hand term in (2) cannot increase as $ r \rightarrow R $ more rapidly than $ 2T ( r, f ) $ outside some exceptional set $ E $.
References
| [1] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [2] | R. Nevanlinna, "Le théorème de Picard–Borel et la théorie des fonctions méromorphes" , Gauthier-Villars (1929) |
| [3] | H. Weyl, "Meromorphic functions and analytic curves" , Princeton Univ. Press (1943) |
| [4] | L. Ahlfors, "The theory of meromorphic curves" Acta Soc. Sci. Fennica. Nova Ser. A , 3 : 4 (1941) pp. 1–31 |
| [5] | H. Cartan, "Sur les zéros des combinations linéares de 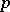 fonctions holomorphes données" Mathematica (Cluj) , 7 (1933) pp. 5–31 fonctions holomorphes données" Mathematica (Cluj) , 7 (1933) pp. 5–31 |
| [6] | P. Griffiths, J. King, "Nevanlinna theory and holomorphic mappings between algebraic varieties" Acta Math. , 130 (1973) pp. 145–220 |
| [7] | V.P. Petrenko, "The growth of meromorphic functions" , Khar'kov (1978) (In Russian) |
Comments
References
| [a1] | W.K. Hayman, "Meromorphic functions" , Oxford Univ. Press (1964) |
| [a2] | P.A. Griffiths, "Entire holomorphic mappings in one and several complex variables" , Annals Math. Studies , 85 , Princeton Univ. Press (1976) |
Nevanlinna theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nevanlinna_theorems&oldid=47963